基于新型机械弹性车轮的整车平顺性分析

汪 伟 赵又群 姜 成 岳红旭 李小龙

南京航空航天大学，南京，210016

0 引言

安全、耐久、经济是对汽车轮胎的基本要求，其中安全尤为重要。近年以来，随着道路质量的提高和高速公路的发展，车辆的平均行驶速度有了很大提高，但同时与轮胎安全相关的交通事故数量也呈上升趋势，高速公路46%的交通事故是由于轮胎发生故障引起的，仅爆胎一项就占事故总量的70%［1］。普通充气轮胎一旦遭到穿刺或发生爆胎，车辆将会立即丧失机动性。为了改变这种状况，安全轮技术越来越受到轮胎工业的重视。目前常见的安全车轮结构主要有以下三种形式：无充气 TWEEL 车轮［2－3］、无充气蜂窝结构轮胎［4］和弹性车轮［5－6］。

机械弹性车轮是一种特殊的弹性车轮，它打破了传统车轮和轮胎的界线，将车轮与轮胎集成于一体。它采用机械结构与橡胶的弹性取代传统充气结构的弹性，由于采用无充气机械弹性结构，这种车轮理论上不存在现有充气轮胎爆胎、弹伤和爆损等问题，所以它更全面地符合战术车辆的安全性要求。笔者对弹性车轮的研究尚处于初级阶段，为避免试验期间造成财物损失和时间浪费，有必要对弹性车轮与普通子午线轮胎进行平顺性对比分析。本文研究主要针对越野车，所以机械弹性车轮选用与某型越野车匹配的265／70R16轮胎作为参照。

1 车轮系统构成及基本原理

1.1 机械弹性车轮系统构成

本机械弹性车轮是针对某型轮式特种车辆进行设计的，以期替代现在使用的某型子午线充气轮胎［6］。

车轮的初步设计外形如图1所示，车轮内部的弹性钢圈结构如图2所示。机械弹性车轮主要由行驶胶圈、弹性环、弹性环组合卡、轮毂、回位弹簧、销轴、铰链等构成，结构如图1、图2所示。将12个弹性环组合卡等角度分布，以将多根弹性环排列组合锁卡在一起，在橡胶层和帘子布层内埋设预置硫化物形成弹性外轮。将轮毂置于弹性外轮中间，用销轴将12个铰链组的一端径向安装在弹性外轮内侧的弹性环组合卡的销座上，再用螺栓轴将12个铰链组的另一端安装在轮毂的螺栓孔上，这样就基本构成了机械弹性车轮。车辆行驶过程中车身载重、地面冲击以及驱动和制动产生的转矩造成的铰链的弯曲，可通过铰链3下端的回位弹簧回位。

由于此车轮的橡胶部分是实心的，并且除橡胶外圈外其他均是金属结构，因此它具有防爆胎特性与防弹性能。

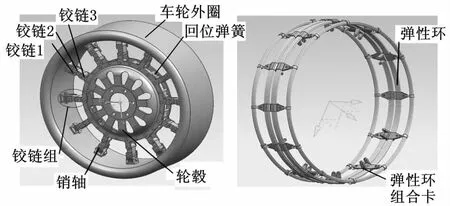
图1 弹性车轮几何模型图 图2 弹簧钢圈结构图

1.2 机械弹性车轮基本原理

车轴传给轮毂的扭矩通过销轴、铰链组以力矩作用拉动弹性外轮做旋转滚动运动，使车辆行驶。轮毂是依靠上部和两侧的铰链组的拉挂微悬于车轮外圈内的，向地面方向有微量下沉，轮毂下面的铰链组因不受力而呈微曲状，弹性外轮上部因受到来自于轮毂的向地面的拉力，使其有设定范畴内的适度的类椭圆的弹性变形，弹性外轮的这种很小幅度的弹性变形，使其接地处的受力面积依设定而远大于轮胎的接地面积，以更有利于减小对地面及对接触面的压强。行驶胶圈的接地处的直线段与相延圆弧为其自适性的相切延形态，与轮胎接地处受力时完全局部的变形形态存在本质的区别，这使其滚动阻抗及其能耗远比轮胎要小很多，即其机械效率远高于轮胎的机械效率。此车轮在装车行驶的滚动运动中，各铰链组均从受拉力渐转至微曲不受力再至受拉力，循环更替周而复始。因为轮毂在其任何瞬时均以微悬态悬于弹性外轮内，来自路面不平度的颠簸只能为弹性外轮所承受，并瞬时随其弹性变形与相应链组的瞬时弯曲所缓解，与正常充气轮胎有着同样的缓冲隔振性能。

2 机械弹性车轮有限元分析

2.1 机械弹性车轮有限元模型

根据1.1节中机械弹性车轮的系统构成，为了保证有限元模型尽可能真实地反映原结构的所有特性，建立机械弹性车轮的有限元模型，如图3、图4所示。其中，弹簧环采用Beam4单元模拟，弹性环组合卡采用MPC184刚性单元模拟，以保证弹性环上各节点自由度的一致。有限元模型中各段轮辐采用MPC184刚性单元模拟。有限元模型中铰链的位置与图1和图2模型中铰链的位置及长度完全一致，并通过耦合节点的方法保证铰链的旋转自由度与实际铰链相同。回位弹簧采用Combin14弹簧单元模拟，轮毂则采用Solid45单元模拟。在建模时充分考虑了橡胶材料的超弹性，胎胶部分采用Solid185单元模拟，胎胶接地部分网格应细化，材料模型采用Mooney－Rivlin橡胶材料。

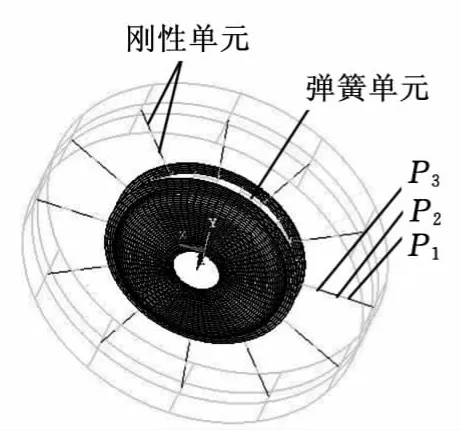
图3 车轮骨架图

图4 车轮网格模型图

轮胎中的橡胶材料能够承受非常大的弹性变形，其应力－应变关系表现出高度的非线性。Rivlin提出最通用的应变能函数如下［7］：

式中，W 为应变能密度；Cijk为Rivlin系数；I1、I2、I3分别为第1、第2、第3Green应变不变量。

Mooney－Rivlin方程［7］给出了一种简单的应力－应变关系曲线，这是一种广泛采用的模式。其表达式如下：

式中，C10、C01为Rivlin系数，均为正定常数。

对于大多数橡胶而言，在应变为150%以内时可得到合理的近似。通过下列经验公式便可获得C10、C01这两个系数：

式中，E 为材料的弹性模量［8］，E＝9.61MPa。

经过 计 算 C10＝1.2813MPa；C01＝0.3203MPa。

2.2 机械弹性车轮有限元分析结果

根据车轮的实际受力情况，分别得出机械弹性车轮和子午线轮胎的径向刚度、侧向刚度和纵向刚度［9］，如表1所示。从表1中可以看出机械弹性车轮的侧向刚度、纵向刚度和径向刚度均比子午线轮胎的大。

表1 机械弹性车轮与子午线轮胎静态刚度对比N／mm

3 整车平顺性仿真对比

本文利用ADAMS对机械弹性车轮进行建模，将有限元仿真结果的各向刚度代入ADAMS自带的轮胎模型中进行修改，从而得到弹性车轮与子午线轮胎模型，最后建立整车模型，分别分析了基于机械弹性车轮的整车仿真结果和普通子午线轮胎车轮的整车仿真结果，比较了两种车轮下的整车平顺性。设定整车在B级路面上以60km／h的速度行驶。将基于机械弹性车轮的整车质心与基于普通子午线轮胎的整车质心的平顺性结果进行对比，得出X 轴方向（纵向）、Y轴方向（侧向）、Z轴方向（径向）的加速度曲线如图5和图6所示。

利用ADAMS后处理的快速傅里叶变换（FFT）功能将各个方向的加速度曲线转变成加速度功率谱密度曲线，然后得到如图7和图8所示的曲线。从图中可以看出：基于机械弹性车轮的整车水平X、Y方向加速度功率谱密度的峰值分别出现在4.5Hz和12Hz位置附近，避开了0.5～2Hz的人体对振动频率敏感的范围［10］；基于子午线轮胎的整车水平X、Y方向加速度功率谱密度的峰值分别出现在3.6Hz和11.5Hz附近位置，同样避开了0.5～2Hz的人体对振动频率敏感的范围。从图7和图8可以看出，基于机械弹性车轮的整车垂直Z方向加速度功率谱密度的峰值出现在1Hz位置附近，避开了4～12.5Hz的人体对振动频率敏感的范围。基于子午线轮胎的整车垂直Z方向加速度功率谱密度的峰值出现在2.58Hz位置附近，避开了4～12.5Hz的人体对振动频率敏感的范围。

图5 基于机械弹性车轮纵向、侧向、径向的加速度曲线图

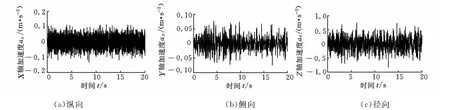
图6 基于子午线轮胎纵向、侧向、径向的加速度曲线图

图7 基于机械弹性车轮纵向、侧向、径向的加速度功率谱密度曲线图

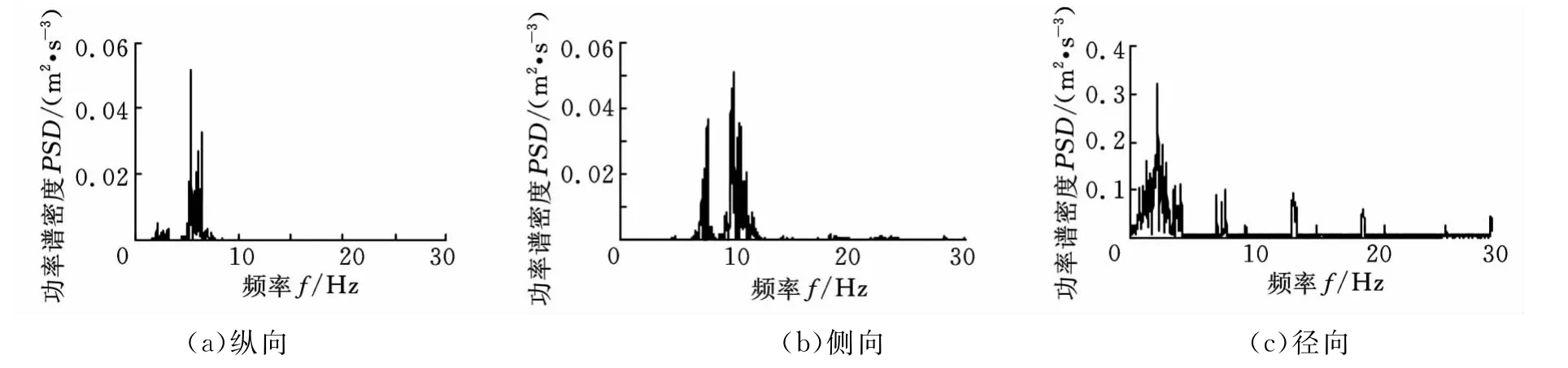
图8 基于子午线轮胎纵向、侧向、径向的加速度功率谱密度曲线图

以上的分析表明，机械弹性车轮在平顺性方面可以达到替代传统子午线轮胎的效果。根据ISO2631－1：1997（E）标准规定，采用下式来得到各轴向的频率加权函数Wk（f）［10］：

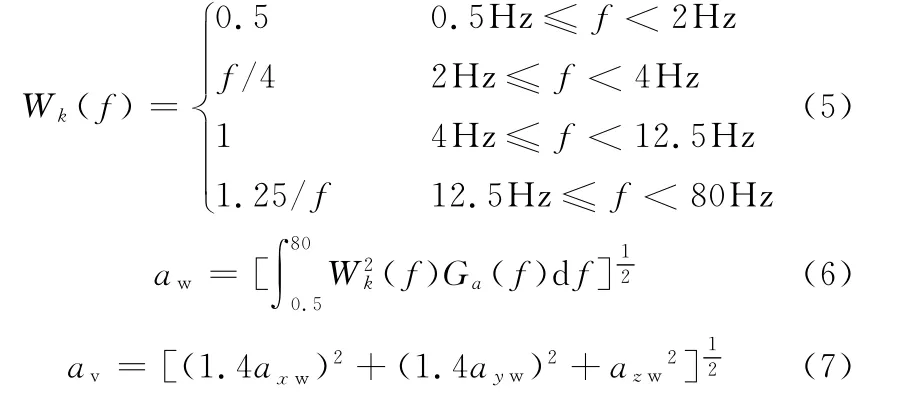
根据式（6），在ADAMS后处理中计算出各轴向的加权加速度均方根值，计算结果如图9～图11所示。从图中可以读出各轴向在80Hz的加权加速度均方根值，然后对其开平方，即可得到各轴向的加权加速度均方根值axw、ayw、azw，然后根据式（7）计算出总加权加速度均方根值av。其中，Ga（f）为功率谱密度函数，aw为加权加速度均方根值。

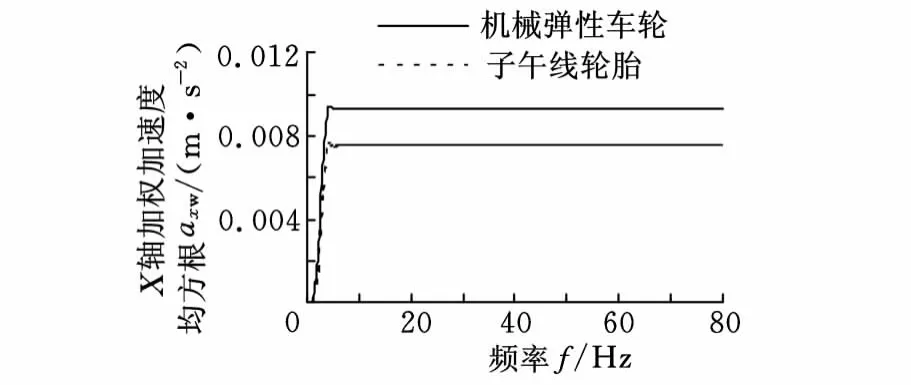
图9 X轴向加权加速度均方根值计算结果

图10 Y轴向加权加速度均方根值计算结果

以相同的方法，可以计算出整车在车速为40km／h，50km／h，60km／h，70km／h时的各轴向加权加速度均方根值和总加权加速度均方根值，结果如表2和表3所示。

图11 Z轴向加权加速度均方根值计算结果

表2 基于机械弹性车轮的整车不同车速下的加权加速度均方根值

表3 基于子午线轮胎的整车不同车速下的加权加速度均方根值

从表2、表3中可以看出：①随着车速的提高，加权加速度均方根值变大，即整车的行驶平顺性随着车速的提高有所降低；不同车速下，基于子午线轮胎的整车平顺性略优于基于机械弹性车轮的整车平顺性，但是基于机械弹性车轮的整车满足普通轮胎的平顺性规律，符合轮胎的特性。②由加权加速度均方根值和人的主观感觉可知：当加权加速度aw小于0.315m／s2时，人体没有不舒适［10］。该整车无论是基于机械弹性的车轮还是子午线轮胎，当车速低于60km／h时，在B级路面上行驶时人体没有感觉不舒适。但是由于机械弹性车轮致力于提高整车的操纵稳定性，所以在当整车基于机械弹性车轮以70km／h行驶时，驾驶员座椅的振动响应略微超过限值，人体有一些不舒服；而当整车基于子午线轮胎以70km／h行驶时，驾驶员座椅的振动响应未超过限值，人体没有感觉不舒适。即表明高速情况下，基于机械弹性车轮的整车平顺性有待进行一步改进。

4 结语

车辆的支承、导向和操纵要通过轮胎与地面之间的相互作用来实现，其作用性能影响着汽车整车的安全性。本文主要为了提高越野车辆的安全性能，参照现有的充气轮胎，提出了一种用于某型越野车辆的机械弹性车轮。通过基于机械弹性车轮与普通子午线轮胎的整车平顺性对比分析，得出基于子午线轮胎的整车平顺性略优于基于机械弹性车轮的整车平顺性的结论，这为机械弹性车轮的改进设计提供了理论指导。

［1］佟金，杨欣，张伏，等.零压续跑轮胎技术现状与发展［J］.农业机械学报，2007，38（3）：182－187.Tong Jin，Yang Xin，Zhang Fu，et al.Development of Run－flat Tire Technology［J］.Transactions of the Chinese Society for Agricultural Machinery，2007，38（3）：182－187.

［2］Ramachandran M.Nonlinear Finite Element Analysis of Tweel Geometric Parameter Modifications on Spoke Dynamics during High Speed Rolling［D］.South Carolina：Univ.of Clemson，2008.

［3］Bezgam S.Design and Analysis of Alternating Spoke Pair Concepts for a Non－Pneumatic Tire with Reduced Vibration at High Speed Rolling［D］.South Carolina：Univ.of Clemson，2009.

［4］Ma J，Ju J，Summers J D，et al.Effects of Cellular Shear Bands on Interaction between a Non－pneumatic Tire and Sand［C］／／SAE 2010World Congress＆Exhibition.Detroit：SAE，2010：598－606.

［5］管欣，王鹏，詹军，等.金属弹性车轮的建模与动态仿真研究［J］.中国机械工程，2007，18（21）：637－641.Guan Xin，Wang Peng，Zhan Jun，et al.Modeling and Dynamic Analysis of a Metal Elastic Wheel［J］.China Mechanical Engineering，2007，18（21）：637－641.

［6］赵震东.悬毂輮式车轮：中国：200510089076.7［P］.2009－05－27.

［7］Meschke G，Helnwein P.Large－strain 3DAnalysis of Fiberreinforced Composites Using Rebar Element：Hyperelastic Formulation Forcord［J］.Computational Mechanics，1994，13（4）：241－245.

［8］李辉.子午线轮胎充气及静态接触状态下的有限元分析［D］.武汉：华中科技大学，2006.

［9］臧孟炎，许玉文，周涛.三维非线性轮胎的五刚特性仿真［J］.华南理工大学学报（自然科学版），2011，39（1）：129－133.Zang Mengyan，Xu Yuwen，Zhou Tao.Characteristics Simulation of Five Kinds of Stiffness of Tire Based on Three－dimension Nonlinear Model［J］.Journal of South China University of Technology（Natural Science Edition），2011，39（1）：129－133.

［10］余志生.汽车理论［M］.5版.北京：机械工业出版社，2009.