瑞利型声板波的液体传感研究

阮 鹏 陈智军，2 张亦居 王萌阳 蒋 玲

1.南京航空航天大学，南京，210016 2.南京大学近代声学教育部重点实验室，南京，210093

0 引言

声板波（acoustic plate mode wave，APM）是一种在板状固体结构中传播的弹性波，可利用沉积在足够薄的压电基片表面的叉指换能器（inter－digital transducer，IDT）来有效激发［1－2］。当采用声板波器件进行液体检测时，可选择IDT沉积在基片其中一个界面而待测液体与另一界面接触的结构形式，使得IDT与液体分离开来，不受液体侵蚀［3－4］。与此同时，声板波也不会因为液体的出现而产生太大衰减［5－6］。因此，声板波器件非常适于液体传感［7－9］。

本文以传播方向和基片表面法线方向存在振动的瑞利型声板波为例，在有限元软件COMSOL中建立了声板波的二维模型，仿真分析了声板波在自由空间中和负载液体时的特征频率，并通过实验证明了理论模型的正确性和数值仿真的有效性，研究结论可以为声板波液体传感器的设计提供指导。

1 理论建模

声板波器件是一种典型的谐振式器件，特征频率是器件的主要参数［10］。当声板波器件用作液体传感时，主要通过特征频率随液体特征参数的变化来实现检测功能［11］。在有限元分析中，模态是机械结构的固有振动特性，每一个模态具有特定的特征频率和模态振型。因此，通过有限元软件COMSOL的模态分析模块可建立声板波器件的理论模型，从而分析其频率特性。

声板波器件的结构如图1所示。IDT沉积在压电基片表面，由周期性排列并与汇流条交替连接的多对电极构成。图1中，x1正方向为声波传播方向，x2正方向为水平剪切方向，x3正方向为基片表面法线方向。由于瑞利型声板波只在x1方向和x3方向存在振动位移［12］，因此可将器件简化为弧矢平面（x1－x3平面）上的二维模型。利用声板波的周期性边界条件，可把IDT简化为由一对电极组成的周期结构，从而减小计算量。基于上述分析，声板波器件可简化为如图2所示的二维坐标系。基片表面用于声波激发，基片背面用于液体传感，基片厚度为d。由于声板波器件的压电基片足够薄，待测液体可视为半无限结构。

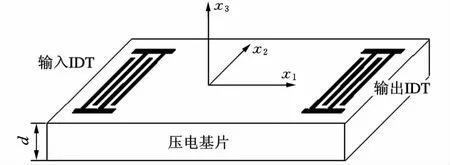
图1 声板波器件结构

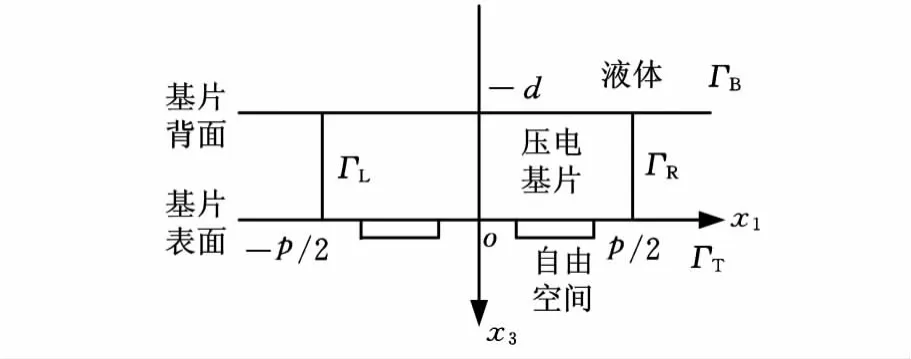
图2 声板波器件坐标系

压电材料选择YZ－LiNbO3，其密度ρ＝2700kg／m3，对应的欧拉角为（0°，90°，90°），在该切向和传播方向上激发出的声板波只在弧矢方向上存在振动，为瑞利型声板波；IDT采用金属铝电极，其密度ρIDT＝2700kg／m3，弹性模量 E＝70GPa，泊松比ν＝0.33，IDT的周期p与声板波波长λ一致；液体选择为纯水，其密度ρL＝1000kg／m3，体积弹性模量CL＝2.19GPa，相对介电常数εL＝80。声板波器件的几何尺寸如表1所示。

表1 声板波器件几何尺寸

声板波器件二维模型的边界条件如下：①基片表面边界条件ΓT为自由边界条件；②基片背面边界条件ΓB为自由边界条件或金属边界条件（电势Φ＝0）；③左右边界条件ΓL、ΓR为一对周期性边界条件，即左右边界上对应节点的3个自由度（x1方向位移u，x3方向位移v，电势Φ）相等。

2 数值仿真

在实际应用中，通常通过IDT来有效激发声板波。如果不考虑声板波激发原理，仅分析其传播时需要满足的边界条件，同样可以通过COMSOL的模态分析模块来研究无电极压电基片结构的声板波频率特性，此时只需在上述图2模型中去掉叉指电极即可。

针对自由空间（基片不负载液体，表面与背面都与自由空间接触）的声板波，当基片背面为自由边界条件时，无电极压电基片的声板波振型如图3所示。由于声板波的色散效应，此时会有A0（0阶反对称模态）和S0（0阶对称模态）两个模态，分别如图3a、图3b所示，其特征频率分别为1.636MHz、6.851MHz。图3中右边的颜色刻度表示振动位移大小，颜色从上到下表示振动位移逐渐减小。当基片背面为金属边界条件时，无电极压电基片的声板波振型与图3类似，同样存在A0和S0两个模态，特征频率分别为1.632MHz、6.771MHz。

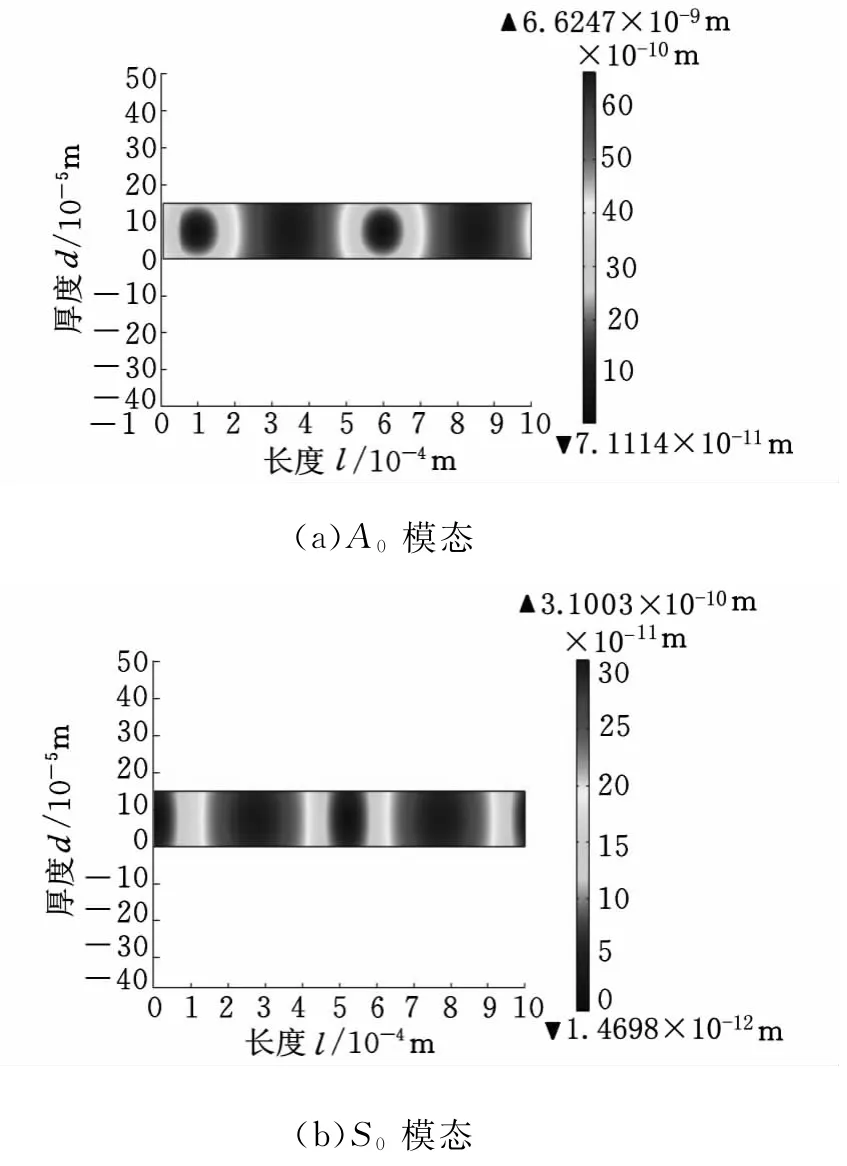
图3 自由空间的声板波振型

当压电基片表面沉积叉指电极时，基片背面为自由边界条件的A0和S0模态的特征频率分别为 1.622MHz、6.615MHz，比无电极时的1.636MHz和6.851MHz小，这是由IDT的质量加载效应引起的。与之相似，基片背面为金属边界条件的A0和S0模态的特征频率分别为1.618MHz、6.545MHz，同样比无电极时的1.632MHz和6.771MHz小。

压电基片背面分为两种边界条件。对于自由边界条件，压电基片界面上不可能有自由电荷，其电荷密度为零；对于金属边界条件，其界面的电势Φ＝0。在实际制作中，由于压电材料是不导电的，通常通过在基片上溅射一层足够薄的接地金属薄膜，以实现电势为零的金属边界条件［13］。在COMSOL中建立基片背面覆盖金属薄膜的模型如图4所示，薄膜材料为金，厚度为10μm。

图4 基片背面覆盖金属薄膜模型

通过COMSOL仿真可知，基于图4的模型同样可激发出A0与S0模态，特征频率分别为1.618MHz和6.545MHz，与基片背面为金属边界条件时完全一致。上述仿真进一步证明：对于压电基片的金属边界条件，可通过在界面上镀上一层接地的可忽略厚度影响的金属薄膜来实现。

对于负载液体（基片表面与自由空间接触，背面负载液体）的声板波器件，当基片背面为自由边界条件时，负载纯水的声板波振型如图5所示。此时同样存在A0和S0两个模态，分别如图5a、图5b所示，其特征频率分别为1.378MHz和6.126MHz。与自由空间的1.622MHz和6.615MHz相比，声板波负载液体时，A0和S0模态特征频率发生了显著变化，从而可用于液体的特征参数检测。

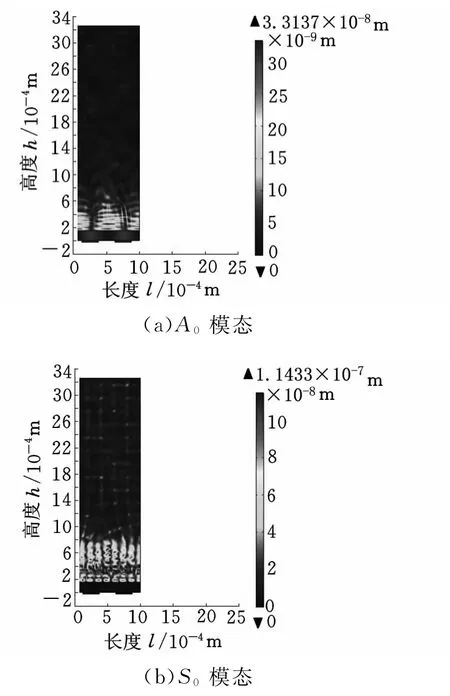
图5 负载纯水的声板波振型

从图5可以看出，总的说来，液体只在与基片背面接触的界面以上一到两个波长内存在着比较明显的振动位移。当液体深度超过两个波长之后，声板波的特征频率几乎不受液体深度的影响。因此，上述仿真进一步表明，可将声板波器件负载的液体视为半无限结构。图5b与图5a相比，液体即使在基片背面以上超过两个波长（2mm）的范围也有着一定的振动，表明S0模态负载液体时产生了一定的衰减，因此A0模态比S0模态更适于液体传感。当基片背面为金属边界条件时，负载纯水的声板波振型与图5相似，特征频率分别为1.377MHz、6.125MHz，并且S0模态同样产生了衰减。

为便于比较和分析，综合上述仿真结果，各种器件结构对应的声板波A0和S0模态特征频率值可归纳如表2所示。

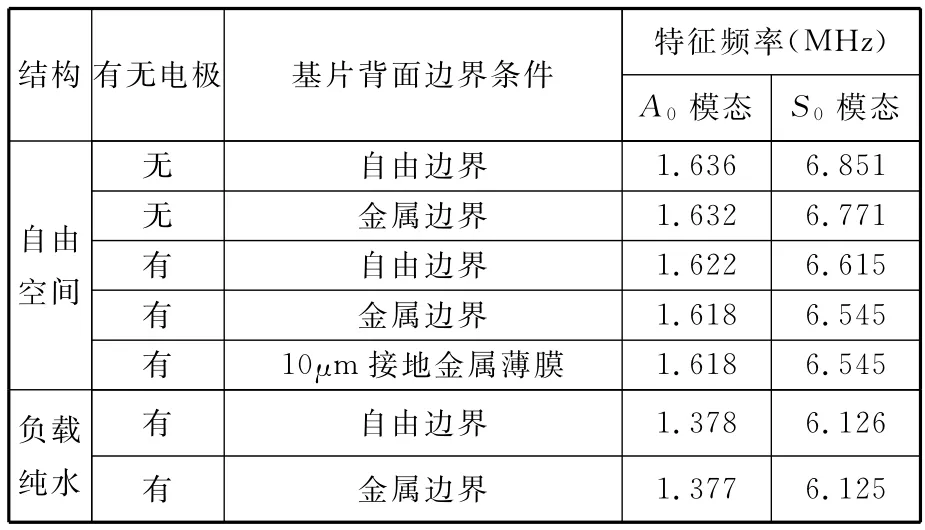
表2 声板波器件模态仿真结果

3 实验分析

按照表1的几何尺寸实际制作了两组声板波器件。其中一组器件的基片背面为自由边界条件；另一组则为金属边界条件，在基片背面溅射了一层10μm的金属薄膜并接地。根据叉指周期p＝1mm，加载液体时液体的深度应大于2mm。在留有余量的情况下，将液槽深度设计为五个波长，即5mm。

采用网络分析仪测量了两组声板波器件在自由空间中与负载纯水时的幅频特性，测量结果如图6所示，从图中可得出A0模态与S0模态的特征频率值。实验结果与数值仿真的对比如表3所示。

由表3可知，当基片背面为自由边界时，自由空间的声板波A0模态实验值与理论仿真值有较大的差别，相对误差为－13.93%。误差较大的原因可能是该模态声板波的机电耦合系数太小，难以有效激发。从图6a也可以看出，此时的A0模态并不明显，其插入损耗与周围的杂波相比没有显著的差别。除此之外，实验结果与理论仿真之间的相对误差都在10%以内，表明了理论模型的正确性和数值仿真的有效性。

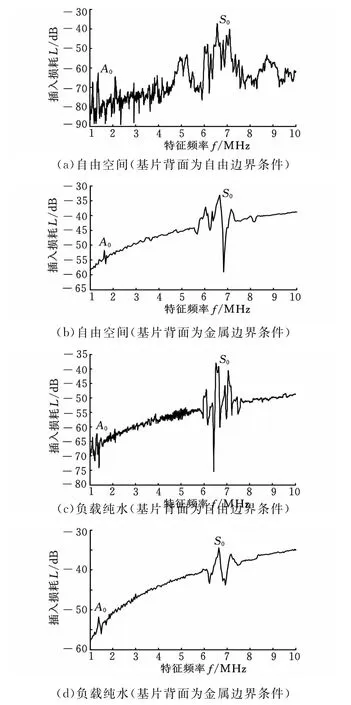
图6 声板波器件的幅频特性

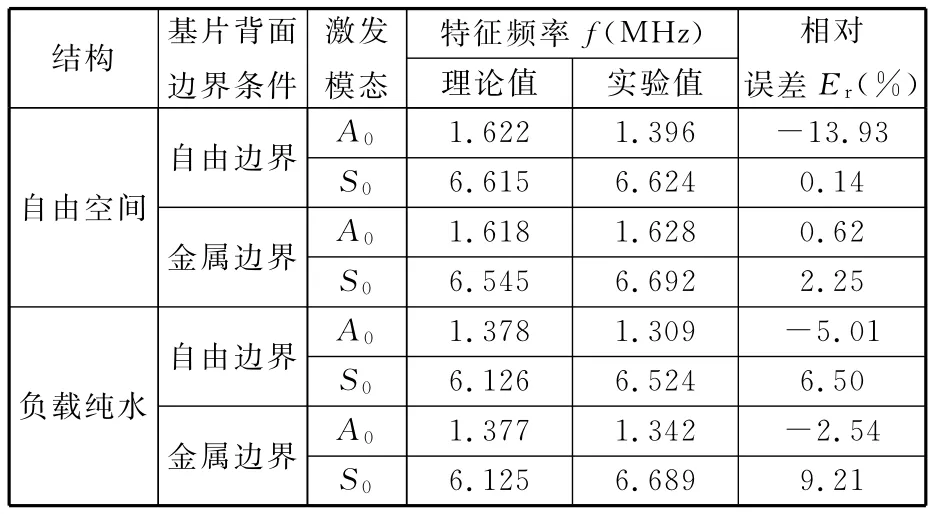
表3 实验结果与数值仿真的对比

4 结论

①无论声板波器件为自由边界条件或金属边界条件，由于IDT的质量加载效应，有叉指电极时的A0与S0模态特征频率值都小于无电极时的相应值。②对于压电基片的金属边界条件，可通过在界面镀上一层接地的可忽略厚度影响的金属薄膜来实现。③无论基片背面为自由边界或金属边界，负载液体时都会导致A0和S0模态特征频率的变化，从而可用于液体的特征参数检测。④由于S0模态负载液体时会产生一定的衰减，因此声板波的A0模态比S0模态更适于液体传感。

［1］陈智军，李良儿，施文康，等.声表面波与声板波激发特性对比研究［J］.中国机械工程，2008，19（11）：1278－1282.Chen Zhijun，Li Lianger，Shi Wenkang，et al.Comparative Study on Excitation Characteristics of Surface Acoustic Wave and Acoustic Plate Mode Wave［J］.China Mechanical Engineering，2008，19（11）：1278－1282.

［2］Anisimkin V I，Voronova N V.Acoustic Properties of the Film／plate Layered Structure［J］.IEEE Transactions on Ultrasonics Ferroelectrics and Frequency Control，2011，58（3）：578－584.

［3］李良儿，陈智军，郑冲.水平剪切板波的液体粘度传感研究［J］.仪器仪表学报，2010，31（5）：1046－1051.Li Lianger，Chen Zhijun，Zheng Chong.Study on Liquid Viscosity Sensing with Shear－horizontal Acoustic Plate Mode Wave［J］.Chinese Journal of Scientific Instrument，2010，31（5）：1046－1051.

［4］Sharma J N，Chand R，Mohamed I A，et al.On the Propagation of Lamb Waves in Viscothermoelastic Plates under Fluid Loadings［J］.International Journal of Engineering Science，2009，47（3）：391－404.

［5］Kuznetsova I E，Zaitsev B D，Joshi S G，et al.Effect of a Liquid on the Characteristics of Antisymmetric Lamb Waves in Thin Piezoelectric Plates［J］.Acoustical Physics，2007，53（5）：637－644.

［6］阳明益，陈继超.有限液体负载下压电平板声板波理论分析［J］.力学学报，2008，40（4）：479－484.Yang Mingyi，Chen Jichao.The Theoretical Analysis of Acoustic Plate Wave in Piezoelectric Plate with Finite Fluid Loading［J］.Chinese Journal of Theoretical and Applied Mechanics，2008，40（4）：479－484.

［7］Feng Li，Wu Yihui，Bastien F，et al.Multi－parameter Sensing in Liquid Using a Lamb Wave Based Microsensor［C］／／2008Symposium on Piezoelectricity，Acoustic Waves and Device Applications，SPAWDA 2008.Nanjing，2008：320－323.

［8］Faustmann H，Munch M，Lindner G，et al.Measurement of the Properties of Liquids Based on the Dispersion of Lamb Waves in an Acoustic Waveguide［C］／／International Congress on Ultrasonics，ICU 2009.Santiago，2010：959－964.

［9］Andle J，Haskell R，Sbardella R，et al.Design，Optimization and Characterization of an Acoustic Plate Mode Viscometer［C］／／The 6th IEEE Conference on Sensors，IEEE Sensors 2007.Atlanta，2007：864－867.

［10］冯冠平.谐振传感器理论及器件［M］.北京：清华大学出版社，2008.

［11］Herrmann F，Jakoby B，Rabe J，et al.Microacoustic Sensors for Liquid Monitoring［J］.Sensors Update，2001，9（1）：105－160.

［12］武以立，邓盛刚，王永德.声表面波原理及其在电子技术中的应用［M］.北京：国防工业出版社，1983.

［13］陈智军.声板波激发特性与液体传感研究［D］.上海：上海交通大学，2007.