基于振动传递率函数和奇异值熵的结构损伤检测方法
2013-09-07程军圣
杨 斌 程军圣
湖南大学汽车车身先进设计制造国家重点实验室,长沙,410082
0 引言
现代工程结构在其使用过程中受载荷及各种突发性因素的影响,往往会产生损伤。这些损伤的积累会导致结构的承载性能的削弱并导致破坏。因此,对结构损伤进行识别,确定损伤的位置及其程度,可以有效保证机组的正常运行,避免发生重大事故。传统的基于结构模态参数识别的损伤检测方法容易受到环境和运行工况的影响,导致诊断的准确率降低[1-2]。近来,有学者直接对测得的动态响应数据进行分析,提取损伤指标。Ruotolo等[3]通过频响函数建立特征参数矩阵,并对其进行奇异值分解,利用奇异值建立损伤指标,对悬臂梁进行了损伤类型的识别。Zang等[4]用神经网络算法直接对所测得的结构频响函数进行分析,以判断结构的状态。Ni等[5]进一步运用主分量分析法对测得的结构频响函数进行降维处理,有效解决了频响函数作为神经网络输入数据量过大的问题。然而,在工程结构的动态识别过程中,激励信号往往是未知的。针对这个问题,Ribeiro等[6]提出了多自由度振动传递率函数的概念,并将其成功用于多自由度系统响应分析。Maia等[7]将振动传递率函数用于损伤识别,通过计算损伤前后各个频率处的振动传递率函数向量的相关性,建立损伤指标来识别自由梁的损伤位置。本文通过结构振动响应求解振动传递率函数,将其在相空间重构来建立特征参数矩阵,对特征参数矩阵求奇异值,根据信息熵的定义构造奇异值熵,通过奇异值熵来评估结构的当前状态。
1 振动传递率函数
振动传递率函数可以通过两个不同位置的响应谱之比求得。对于多自由度系统,设在k点输入单点激振力Fk(s),则振动传递率函数可以表示为
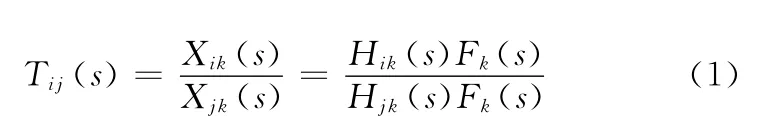
式中,Xik(s)、Xjk(s)分别为第i个自由度和第j个自由度的响应;Hik(s)、Hjk(s)为频响函数。
同样,可以定义结构发生损伤后的第i个自由度和第j个自由度之间的振动传递率函数:


图1 多自由度系统振动传递率函数曲线和频响函数曲线
在实际运用中,类似于频响函数的估计方法,振动传递率函数的估计通常采用H1估计方法[8]:

式中,SX0Xref(s)为输出点响应X0(s)与参考点响应Xref(s)的互谱;SXrefXref(s)为参考点响应Xref(s)的自谱。
2 基于振动传递率函数和奇异值熵的结构损伤检测方法
当结构出现损伤时,其振动传递率函数将发生变化,因此可以根据振动传递率函数的变化来表征结构的损伤情况。对振动传递率函数组成的特征参数矩阵进行奇异值分解,相当于将其映射到线性无关的特征空间;根据信息熵的定义构造奇异值熵。奇异值熵的大小反映了结构状态的差别,因此可以通过奇异值熵来评估结构的当前状态[9]。
假设结构的振动传递率函数的离散序列T(w)= [T(w1)T(w2) …T(wk)],利用延时嵌陷技术,可以将原始序列映射到相空间中。选定分析模式窗口的长度为m,时延常数为τ,构造新的n×m维的相空间A:
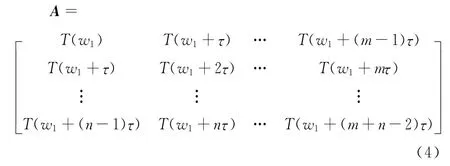
对矩阵A进行奇异值分解,得到奇异值δ1≥δ1≥ … ≥δs,s= min(n,m)。奇异值熵的定义为

式中,pi为第i个奇异值在整个奇异值序列中所占的比重。
由定义可以看出,奇异值熵反映了信号的能量分布情况。当结构发生损伤时,奇异值熵也会相应发生变化,因此可以用它来表征结构的状态和损伤情况。
3 基于振动传递率函数的奇异值熵在结构损伤检测中的应用
为了验证该方法的有效性,本文采用基准结构——三层书架结构为测试对象,该结构由美国Los Alamos国家实验室搭建并进行实验数据的采集。实验数据及结构的详细信息可由Los Alamos实验室网站获得,该结构被广泛运用于结构损伤检测方法研究[10-12]。如图2所示,该结构有3层,每一层的板件由螺栓固定在支架上,分别在板件的4个角处安放传感器,节点编号为A、B、C、D,每个节点处布置2个传感器,整体结构共布置了24个振动加速度计。激振器连接在底层板的D节点位置,实验时采用白噪声激励。时域信号采样点数N=8192,采样频率fs=1600Hz。
如表1所示,在基准结构上设置不同的结构损伤模式。为了验证该方法在不同工况下的适用性,分别设置激振器输入电压为2V、5V和8V(工况C1、C2、C3),每种情况下重复采集数据2次,如表2所示。按式(3)可求取振动传递率函数Tij。

图2 三层书架结构实验装置

表1 三种结构损伤模式

表2 三种不同工况下的测试
对计算得到的振动传递率函数序列,采用延时嵌陷的方法将原序列在相空间重构。其中,延迟时间τ和嵌入维数m为两个重要的参数,直接影响重构后的相空间与原序列的等价关系。为了计算这两个参数,本文采用C-C相空间重构方法[13],计算结果如表3所示。按式(4)构造相空间A,对A进行奇异值分解,按式(5)计算得到奇异值熵。

表3 相空间重构延迟时间τ和嵌入维数m
为分析不同的测点对奇异值熵的影响,在同一工况下,选择D3损伤模式,工况为C3,选取D1点为参考点,分别计算点A2、B2、C3、D3处的振动传递率函数,经相空间重构及奇异值分解后的奇异值结果如图3所示。由图3可知,不同振动传递率函数之间的奇异值不相同,但是经过计算发现,在同一状态下,不同测点之间的振动传递率函数的奇异值熵几乎不变。为了研究不同测点之间振动传递率函数对奇异值熵的影响,在不同的结构状态下进行了大量的计算。结果表明,不同测点之间的振动传递率函数只会改变奇异值的大小,不影响奇异值熵的值。因此,奇异值熵可以作为判断结构状态的一个指标。选择D1和B3之间的振动响应计算振动传递率函数T13,并计算奇异值熵。通过对比奇异值熵的大小来判别结构的损伤模式。不同实验工况下的振动传递率函数奇异值熵如图4~图6所示。
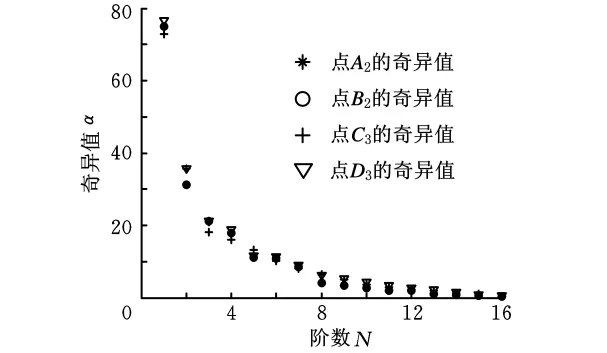
图3 不同测点的奇异值

图4 工况C1下不同损伤模式的奇异值熵
从图4~图6可以看出,在同一种损伤模式下,结构的振动传递率函数的奇异值熵几乎是不变的。奇异值熵对损伤类型十分敏感,损伤与未损伤时的奇异值熵各不相同,而且在不同的损伤模式下,奇异值熵也有明显的差异。通过比较奇异值熵的大小,可以准确识别结构的损伤类型。

图5 工况C2下各损伤模式的奇异值熵

图6 工况C3下各损伤模式的奇异值熵
4 结语
为了对激励未知情况下的结构损伤进行检测,提出了基于振动传递率函数和奇异值熵的损伤检测方法,将振动传递率函数序列在相空间重构,进一步对其进行奇异值分解,通过奇异值熵来判断结构损伤的类型。这种方法直接根据结构响应进行分析,不需要进行模态参数识别,也不需要激励的信息。实验结果表明,基于振动传递率函数和奇异值熵的结构损伤检测方法能有效地应用于结构损伤检测。但是,将振动传递率函数应用到损伤检测方法的研究,尚处于起步阶段。目前提出的方法局限于单一稳定工况、单点激励,将其推广至非平稳、多点激励工况,仍有许多工作需要做。
[1]Alvandi A,Cremona C.Assessment of Vibrationbased Identification Techniques Damage[J].Journal of Sound and Vibration,2006,292(1/2):179-202.
[2]Doebling S W,Farrar C R,Prime M B.A Summary Review of Vibration-based Damage Identification Methods[J].The Shock and Vibration Digest,1998,30(2):91-105.
[3]Ruotolo R,Surace C.Using Svd to Detect Damage in Structures with Different Operating Conditions[J].Journal of Sound and Vibration,1999,226(3):425-439.
[4]Zang C,Imregun M.Combined Neural Network and Reduced FRF Techniques for Slight Damage Detection Using Measured Response Data[J].Archieve of Applied Mechanics,2001,71(8):525-536.
[5]Ni Y Q,Zhou X T,Ko J M.Experimental Investigation of Seismic Damage Identification Using PCA-compressed Frequency Response Functions and Neural Networks[J].Journal of Sound and Vibration,2006,290(1/2):242-263.
[6]Ribeiro A M R,Silva J M M,Maia N M M.On the Generalisation of the Transmissibility Concept[J].Mechanical Systems and Signal Processing,2000,14(1):29-35.
[7]Maia N M M,Raquel A B.Damage Detection and Quantification Using Transmissibility[J].Mechanical Systems Signal Processing,2011,25(7):2475-2483.
[8]Devriendt C,Steenackers G,Sitter G,et al.From Operating Deflection Shapes Towards Mode Shapes Using Transmissibility Measurements[J].Mechanical Systems and Signal Processing,2010,24(3):665-677.
[9]于德介,陈淼峰,程军圣,等.基于EMD的奇异值熵在转子系统故障诊断中的应用[J].振动与冲击,2006,25(2):24-26.Yu Dejie,Chen Miaofeng,Cheng Junsheng,et al.Fault Diagnosis Approach for Rotor System Based on EMD Method and Singular Value Entropy[J].Journal of Sound and Shock,2006,25(2):24-26.
[10]da Silva S,Dias M,Lopes V,et al.Structural Damage Detection by Fuzzy Clustering[J].Mechanical Systems and Signal Processing,2008,22(7):1636-1649.
[11]Clement A,Laurens S.An Alternative to the Lyapunov Exponent as a Damage Sensitive Feature[J].Smart Materials and Structures,2011,20(2):025017.
[12]Zang C,Friswell M I,Imregun M.Structural Damage Detection Using Independent Component Analysis[J].Structural Health Monitoring,2004,3(1):69-83.
[13]郑慧峰,吕江明,张斌,等.基于FastICA的超声A波信号降噪研究[J].中国机械工程,2012,23(10):135-1139.Zheng Huifeng,LüJiangming,Zhang Bin,et al.Research on Noise Reduction for A-Wave Ultrasonic Signals Based on FastICA[J].China Mechanical Engineering,2012,23(10):1135-1139.
