Friedman M检验平均秩的多重比较在SPSS软件的实现*

兰州大学公共卫生学院流行病与卫生统计学研究所 申希平 祁海萍 刘小宁

Friedman M检验平均秩的多重比较在SPSS软件的实现*

兰州大学公共卫生学院流行病与卫生统计学研究所 申希平 祁海萍 刘小宁△

△通信作者:刘小宁，E-mail:liuxn@lzu.edu.cn

完全随机区组设计的秩和检验(Friedman’s test)是随机化区组设计方差分析不满足方差分析条件时采用的方法。随机化区组设计的秩和检验是由M·Friedam在符号检验的基础上提出来的，又称M检验，目的是推断各处理组样本分别代表的总体分布是否不同〔1〕。对于Friedman M检验，在当P＜α(α为检验水准)差异有统计学意义时，可认为多个总体间相比较有差异，但不能说明任何两个总体间均是有差异的。通常，研究者更想知道究竟是哪两个组之间有差异，哪两个组之间无差异，此时需要做多重比较。目前，尚无书籍或文献介绍Friedman M检验的组间两两比较在SPSS软件中的实现过程〔2－3〕。本研究的目的是通过SPSS中的菜单操作(限于SPSS18.0及以上版本)和编写程序两种方式，实现Friedman M检验的组间多重比较。

实例〔4〕:8名受试对象在相同实验条件下分别接受4种不同频率声音的刺激，他们的反应率(%)资料见表1。问4种频率声音刺激的反应率是否有差别?

表1 8名受试对象对4种不同频率声音刺激的反应率(%)比较

SPSS菜单操作的方式

1．将数据输入SPSS 19.0软件，输入格式见表2。

2．Friedman M检验。步骤为:

(1)Analysis→Nonparametric Test→Related Samples…，弹出 Nonparametric Tests:Two or More Related Samples对话框。

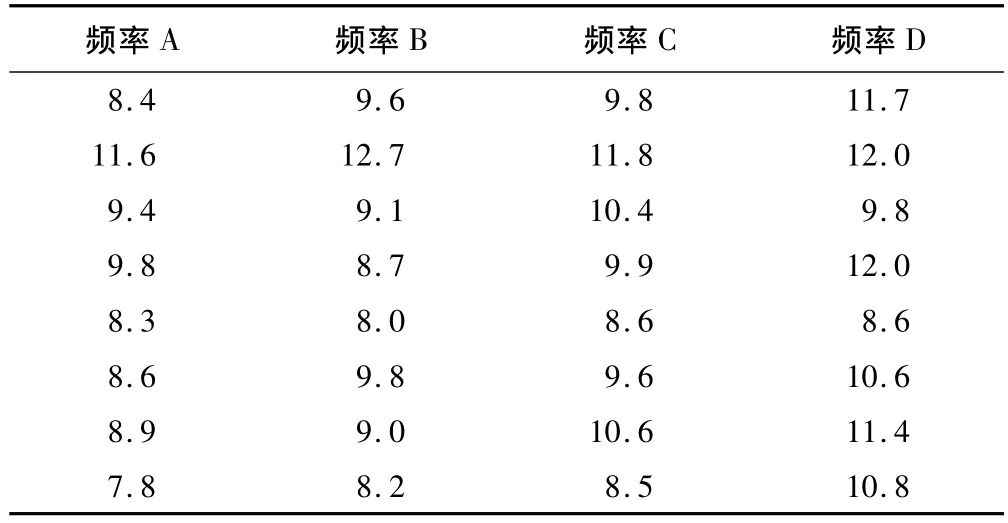
表2 实例数据输入格式

(2)在Fields标签中，将变量“频率A、频率B、频率C、频率”移入Test Fields:栏中。

(3)在Settings标签中，左边的Select an item:栏中选择Chosen Tests，右边选择Customize tests，复选框中勾选 Friedman’s 2-way ANOVA by Ranks(k samples)，multiple comparisons:下拉框选择 All pairwise。

(4)点击Run按钮，即可得到运行结果。

(5)点击运行结果“Hypothesis Test Summary”并单击右键，选择Edit Content→In Separate Window，结果窗口将变为Model Viewer窗口(图1)。

(6)从该窗口可得到:Friedman M检验M=15.152，自由度=3，P=0.002，说明不同频率的反应率有差异。需进行两两比较;频率A的平均秩MRA=1.38，MRB=2.00，MRC=2.94，MRD=3.69。

(7)在该窗口下方的View:下拉菜单中选择Pairwise Comparisons，则出现两两比较结果(表3)。

(8)由表3的概率(Sig.列)可得:频率A和频率C，D有差异，频率B和频率D有差异(P＜0.05);由调整概率(Adj.Sig列)可得:仅频率A和频率D有差异(P=0.002)。

SPSS编程的方式

1．公式

多个相关样本两两比较的q检验〔4〕，公式为:

图1 Model Viewer窗口

表3 两两比较结果

2．程序

(1)打开SPSS的程序编辑窗口(syntax Editor，File→New→Syntax)，输入表4程序。

3．程序说明

第1行:变量定义。

Num:行的编号。最大值(本例为6)可理解为两两比较次数。

表4 多个相关样本两两比较的q检验

n:区组数，也即样本含量。本例n=8。

g:处理组数。本例g=4。

g_MeanRank:每组平均秩。

I_MeanRank:第I组平均秩。

J_MeanRank:第J组平均秩。

第2行:输入数据。

第3～4:计算比较两组的秩和。公式为Ri=n*平均秩。

第5～14:计算公式(2)中的∑R2i。

第16行:按照公式(2)计算MS误差。

第17行:按照公式(1)计算q值。

第19行:将运行结果删除不需要的中间结果后保存在‘d:/friedman．sav’。

第20行:打开‘d:/friedman.sav’数据文件。见表5。

4．运行结果

运行结果中q值的结果与文献〔4〕的结果基本一致。查q界值表，所得结论与文献〔4〕完全一致。

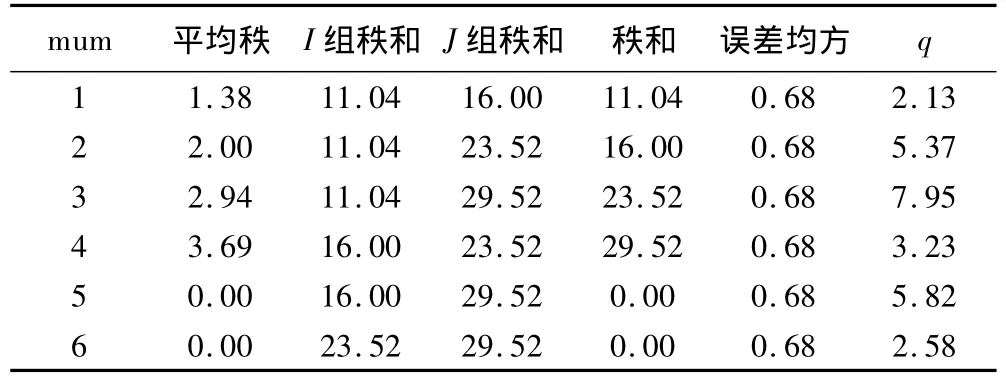
表5 多个相关样本q检验程序运行结果

菜单方式与编程方式结果比较

菜单操作方式的分析结果提供了2个概率值，即直接运算结果概率和调整的概率P(Adj.P)。程序操作按照文献中多个相关样本两两比较的q检验公式的计算过程编写程序，其运行结果与软件菜单操作的结果基本一致，与文献〔4〕查q界值表得到的概率更为接近(表6)。

表6 菜单方式与程序方式结果比较

讨 论

Friedman M 检验平均秩的多重比较，在SPSS18.0及以上版本中已经可以通过菜单操作实现，但在低版本中无法得到多重比较的结果。本研究通过编程方式进行Friedam M检验的多重比较，结果与高版本菜单运行结果一致，很好地解决了SPSS软件对Friedam M检验的多重比较问题。

结果显示，SPSS编程方式和菜单操作结果稍有不同，如频率B与C的比较结果不一致。这是因为两者所用的两两比较的方法不同。在编程方式中，秩次间的多重比较用的是SNK-q检验。而SPSS菜单方式中，统计量的构建如下〔5〕:

如在表3的运行结果中，频率A与频率B“Test Statistic”的值为两平均秩次之差(1.38－2.00=－0.625)，为公式(3)的分子，“Std Error”的值计算公式见公式(4)，为0.645，因此“Std.Test Statistic”的值为TAB=－0.625/0.645=－0.968，TAB服从标准正态分布，利用 SPSS提供的 CDF.NORMAL(Z，0，1)函数可以计算出P=2*(1－φ|Z|)=0.3482，与0.333接近。同时，为减少I类错误的发生概率，对概率P进行调整，调整的概率公式为:P*=P*g(g－1)/2。对于频率A与B比较的调整概率值为0.33*4(4－1)/2=1.98＞1，故直接置为1〔5〕。与直接计算的概率值相比较，调整后的概率值皆偏大，这主要是由于考虑到随着两两比较次数的增加，发生I类错误的概率会增加，研究者在下结论时，可结合专业知识进行权衡。

1．颜虹主编．医学统计学第2版．北京:人民卫生出版社，2010:178-179．

2．孙红卫，王玖，韩春蕾．基于Monte Carlo模拟的非参数多重比较方法评价．中国卫生统计，2011，28(5):501-504．

3．胡小刚，陈剑鸿，刘凤军，等．基于Matlab的Kruskal-Wallis和Nemenyi检验的界面实现．中国卫生统计，2011，28(4):466-467．

4．孙振球主编．医学统计学第3版．北京:人民卫生出版社，2010:142-145．

5．SPSS 19．0 帮助文件．链接为:http://127．0．0．1:2072/help/index．jsp?topic=/com．ibm．spss．statistics．help/alg_introduction．htm．

．兰州大学中央高校基本科研业务费专项资金(lzujbky－2010－192)

(责任编辑:丁海龙)