地震临界区域尺度与地震预测①

余怀忠，张小涛，张永仙

（中国地震台网中心，北京 100045）

0 引言

近年来，国际上将现代统计物理的理论和方法应用于地震和地震预测问题的研究取得长足进展，已成为物理学和地震学之间的一个活跃的交叉领域［1］。然而地震发生的物理成因虽然早已认识，地震预报却始终是世界性难题，原因在于灾害性地震通常发生在地壳内数公里至数十公里深处，与地震孕育过程相关的介质性质、力学状态和动态演化均很难观测到，难以掌握其规律用于地震预报。一个地震活动强烈的地区通常存在一系列规模不等、力学性质不同的活动断裂带的强烈构造活动，使得地震活动存在明显的不均匀性，复发过程不具有良好的准周期性，也不存在“强度可预报性”或“时间可预报性”模型所预期的性质。由地震观测所得到的资料，诸如地震的空间分布和时间变化等，似乎难以为地震预报提供必要的约束［2］。

事实上地震活动性变化通常是由地壳的构造应力水平决定，大量研究发现中等级地震的活跃性直接与随后发生的大地震震级相关［3－6］，即地震活动性的改变反映了地壳介质的构造应力积累过程。从统计力学的观点来看，孕震区域的演化过程在时间上经历了一个由线性向非线性的变化；在空间上经历了由均匀向局部的变化；内部裂隙经历了由小到大、由少到多的变化；而在整体力学状态上将由稳定状态向不稳定状态变化。Ben－Zion等［7－8］提出，从演化特征来看地震属于一种“间歇性临界现象”，因此地震具有可预报性［9－11］。

在地震预测研究中，一个重要问题是如何恰当的选择地震临界区域，这在很大程度上制约了预报的结果。刘蒲雄［12］曾对70年代发生在我国大陆的10次7级以上地震进行了研究，发现大地震发生前几年中等地震活动性增强现象是相当普遍的，其增强的范围可以远达距离地震中心位置数百公里；Keilis－Borok和Soloviev［13］从地震矩释放加速及其他许多前兆性地震活动模式研究中得到临界区域尺度相当于目标地震断层尺度1：5的比例；而Press和Allen［14］通过研究长程相关更认为前兆相关范围能达到地震线性尺度的100倍；Bowman等［15］则更为量化的提出曲率参数C（幂律拟合均方差与线性拟合均方差之比），并以强震震中为圆心，利用不同半径范围内的地震活动来计算参数C，对于参数C为最小并且指数小于0．8的圆型区域被认为是主震的临界区域。

此外，Yin等［16－17］利用加卸载响应比时间序列演化对地震临界区域进行了定义；Rundle等［18－20］则把统计物理方法应用于地震活动性图像的分析，并宣称可以对加州的地震做出比较好的预测。他们尝试使用综合考虑地震活动“增强”与“平静”的地震活动图像算法，针对各种活动构造区域进行中长期地震危险性概率估算。围绕这一问题，还有研究者［21－23］提出可以根据震前地震断层间相互作用的库仑应力触发关系，确定地震临界区域，看来比较好地解决了统计区域的选择问题。然而，这些方法尽管在一定程度上能够确定大地震发生前的区域应力及地震活动性变化，但是在实际地震预测中对临界区域尺度的估计尚不能达成统一的评价指标。

不同的地震预测模型，在空间区域及时间区域的选择上应该存在一致性，都与地震的能量释放密切相关［24－25］。在本文中，我们尝试使用加卸载响应比（LURR）及震前矩张量加速释放（AMR）两种模型，通过华北地区近40年来的M＞5震例对地震临界区域尺度进行统计研究。

1 加卸载响应比理论（LURR）

加卸载响应比是近年来关于震源区地壳介质破坏 演化规律性 认 识 的 重 要 发 现［16－17，24－26］。 其 基 本 思路借鉴了系统论的方法，通过系统与外部的联系来了解系统的性态，简而言之，即研究系统的输入信号与输出信号之间的关系，或者说研究系统对输入信号的响应，达到了解系统性态的目的。在过去的20年中，加卸载响应比方法的研究已经取得了很大发展，并被广泛应用于地震中短期预测实践［27－31］。研究发现在大地震发生之前数月至数年间，加卸载响应比时间序列通常会发生明显的异常增加［16－17］，这一现象可以被用作为地震发生的重要前兆规律［17，24］。

在地震预测实践时，一定时间窗和空间窗内释放的地震能量通常被作为响应量。加载和卸载过程可根据日月潮汐力在地震破裂面上引起的库仑破坏应力CFS进行判断［32－33］，CFS＞0为加载，CFS＜0则为卸载。这样，加卸载响应比可以定义为加载阶段和卸载阶段能量释放之比：

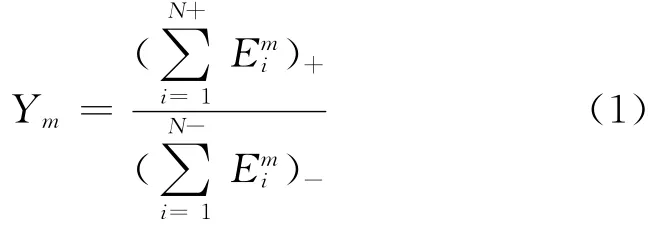
这里Ei表示第i个小地震所释放的能量，m＝0，1／2，或1。当m＝0时，Em就是地震事件数；而当m＝1／2时，Em表示Benioff应变。为了避免地震数目太少造成加卸载响应比时间序列的强烈波动，计算时间窗内通常包含了多个加、卸载循环过程。当孕震区介质处于稳定状态时，LURR在1附近波动，而当地震迫近时，比值会发生明显的变化。

2 矩张量加速释放模型（AMR）

近年来一系列研究表明通常在大地震发生之前地震活动性会出现明显的变化［34］，Bufe和Varnes［35］从损伤力学模型提出一个简单幂律时间－破裂模型可以用来描述这种震前地震活动性变化，他们研究发现1989年美国加州M＝7．0Loma Prieta地震发生前的地震活动可以用下式的幂律关系拟合：

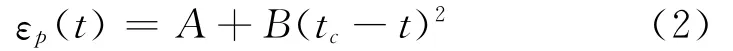
其中，tc表示地震发生的时间，z大约为0．3，能量释放积累过程可以表示为

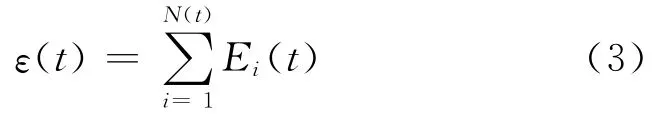
式中，Ei表示第i个地震事件的能量释放，N（t）为t时刻的地震事件数。Sammis和Smith［36］在研究地壳状态的间歇性临界状态时也对这一规律有过类似的发现。按照这一假设大地震可以被看作是一种临界现象，地壳并不一直处于临界状态，当一次大地震发生之后，该地区的地壳将远离临界状态。然后，随着构造应力的逐步增加，地壳介质的相关尺度逐渐增大，该地区的地壳又逐步趋向临界点，而最终地壳介质的相关尺度大小势必与地震发生的震级密切相关。

3 震例分析

运用上述两种模型我们对华北地区近30年来的M＞5地震进行了研究，其中强余震采用Supperseis软件去除［37－39］。统计的震例总数为36。最佳地震临界区域按照如下方法计算：围绕地震震中位置，选取不同半径大小的圆形区域内地震事件的Benioff应变分别计算LURR和AMR时间序列，以确定各模型的最佳地震临界区域。

LURR时间序列按照文献［17］的定义计算。所需的震源机制解由Harvard CMT下载得到。为了统计的客观性，我们只对能得到Harvard CMT的地震进行统计，震例总数15个，其中11个震例在震前观测到明显的异常。如图1所示，我们给出2个震例计算结果，计算的时间窗为1年，滑动时间窗为1个月。从图中可以看到半径不同对应时间序列存在较为明显的差异。震前异常变化最明显的时间序列（如黑色实线所示）所对应的圆形区域就是最佳地震临界区域。

11个震例所得临界区域半径与震级的关系（图2）可以近似拟合为

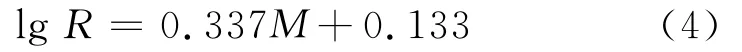
AMR序列及最佳临界区域按照Bowman等［15］的方法计算，即分别采用幂律（式2）和线性两种方法拟合，并计算两种拟合结果的均方差之比R，比值最小的圆型区域被认为是主震的最佳临界区域。若比值R越接近1，则表明能量释放越接近线性过程，即能量释放没有出现明显的加速；如果比值R小于1的程度较大，则表明能量释放过程更接近幂律拟合。在所选择的36个震例中，我们在26个地震发生前观测到如图3所示的能量加速释放过程，拟合得到指数平均值：z＝0．45，这与Ben－Zion和 Lyakhovsky［8］研究的结果类似。26个震例所得临界区域半径与震级的关系（图4）可以近似拟合为

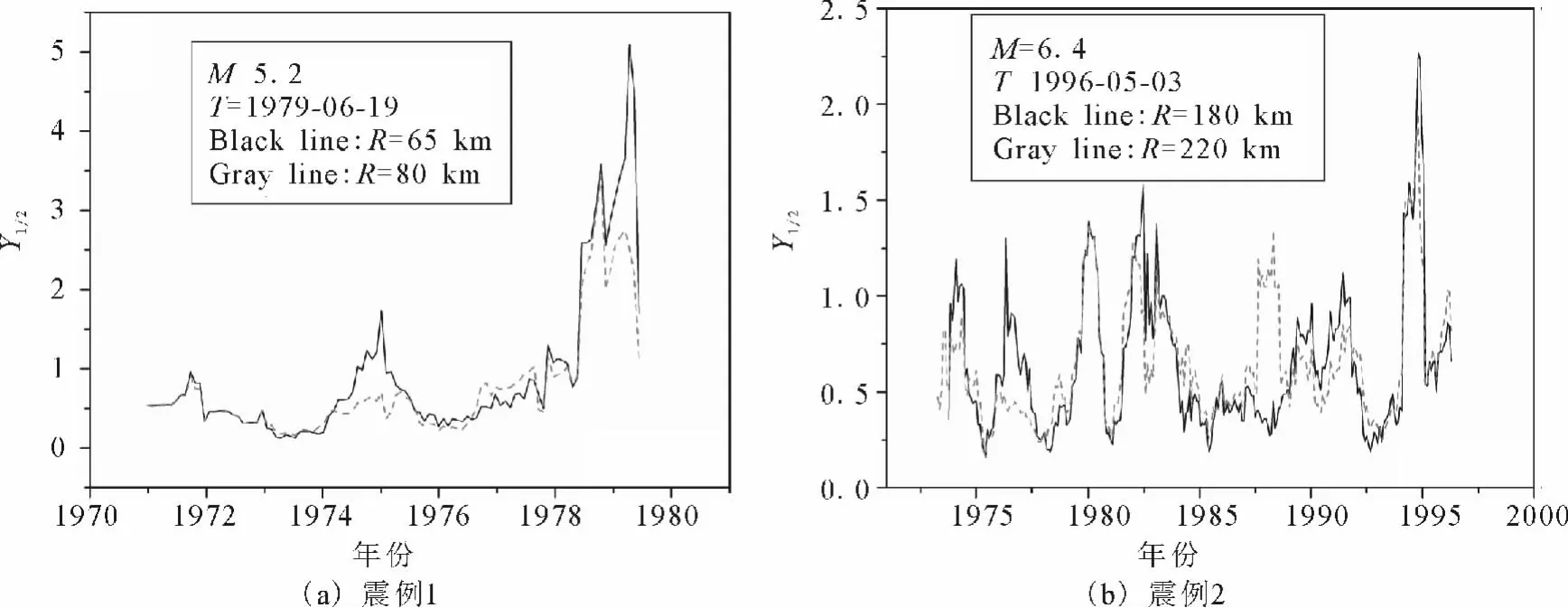
图1 LURR时间序列演化示例图（实线和虚线分别对应不同半径尺度区域的计算结果）Fig．1 Examples of the LURR time series（The black and gray lines denote LURR time series derived from the circular regions with different radius）

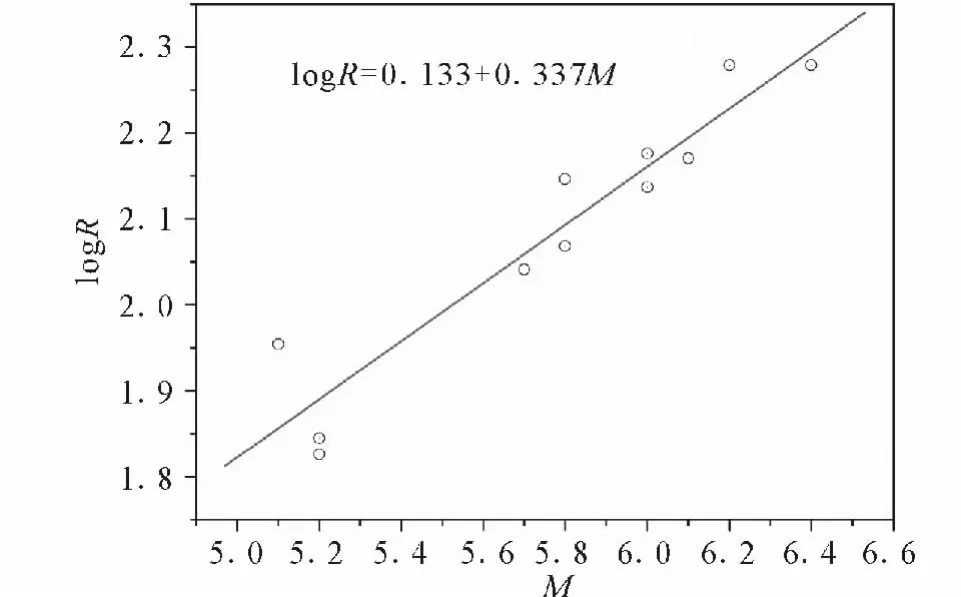
图2 LURR最佳临界区域半径与震级的关系Fig．2 The relationship between radius of the optimal critical region and magnitude of the detection earthquakes for the LURR method

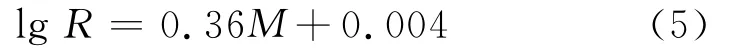
从式（4）和（5）结果可以看到，LURR和 AER两种模型所得临界区域半径R与主震震级之间统计线性关系斜率分别为0．34和0．36，具有明显的一致性。

4 讨论和结论

加卸载响应比（LURR）和矩张量加速释放（AMR）分别反映了灾变发生前临界敏感性的增大以及相关尺度的增加。本文的研究表明，华北地区大部分M＞5地震发生前都能观测到比较明显的LURR和AMR异常，把二者相结合，一起用作为灾变发生的前兆研究，将可能对地震等灾变做出更为准确的预测分析。

LURR是一种中短期地震预测方法，在大部分强震发生前都能观测到LURR时间序列出现明显异常。LURR是依据潮汐力对地震的触发作用计算的，对一个断层而言，如果其周围区域具有较高的库仑应力积累，地震就更容易在这些区域内发生，加卸载响应比的异常变化会更为明显。本文所研究的震例就是这样的情况，震前加卸载响应比的异常变化充分表现出其周围区域的应力积累情况。正因为所选择的最佳地震临界区域是为了研究地震断层上的目标地震而特别设定的区域。那些发生在该区域以外地震事件并没有被纳入加卸载响应比的计算（这些区域应力变化对地震触发的贡献可能并不明显），因而加卸载响应比时间序列变化应该最明显。故此选择响应比值最大的区域为最佳地震临界区域。

强震前的AMR现象已在全球范围不同地区被不同的地震学家所验证过。Turcotte等［40］利用纤维束模型，对材料的能量释放过程进行了研究，在常载荷条件下得到指数z＝1／3；Ben－Zion和Lyakhovsky［8］利用地震数据对z值的变化范围进行了总结，得到z的变化范围为0．1～0．55；Rundle等［18］，Bowman 等［15］，Sornette 和 Sammis［41］等人对指数z的研究也得到了类似的结论。在我们的研究中，平均Z＝0．45，这与文献［8］研究的结果类似。Bowman等［15］通过用幂次率拟合与线性拟合的误差最小给出了一种确定临界区域尺度的最佳估计方法。他们发现二者的比值r一般在0．4～0．6之间，并指出临界区域半径与主震震级之间通常为统计的线性关系斜率约为0．44。我们对华北地区的地震研究结果整体结论是一致的，但斜率要略低，约为0．34和0．36之间，这在一定程度上也反映出构造的差异，为华北地区地震预测研究提供了参考。

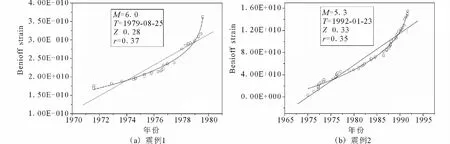
图3 地震发生前的能量释放过程及幂律和线性拟合结果示例（“°”表示Benioff应变累积释放过程，曲线和直线分别表示幂律和线型拟合结果，M：震级，Z：指数，r：均方差之比）Fig．3 Examples of the cumulative Benioff strain and its power－law time－to－failure and linear fits（“°”represents Benioff strain time series，Curve and straight line denote respectively the power－law andlinear fits．M：magnitude，z：exponent，r：the ratio of the residuals to the power－law fit to the residuals of the linear fit）

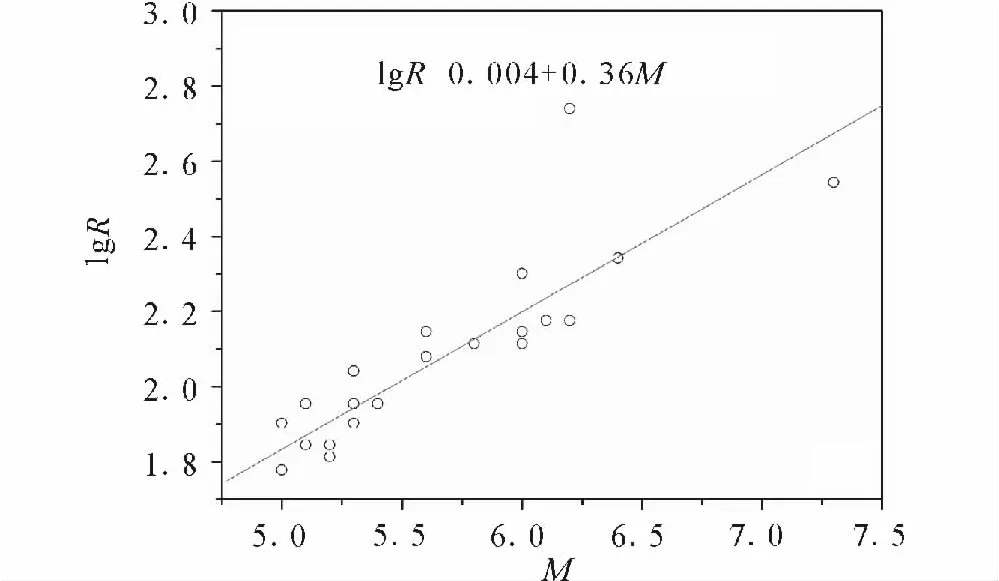
图4 AER最佳临界区域半径与震级的关系Fig．4 The relationship between radius of the optimal critical region and magnitude of the detection earthquakesfor the AMR method

（References）

［1］ 董蕾，杨立明．汶川大震前数字地震仪位移地脉动低频异常现象研究［J］．西北地震学报，2012，34（3）：268－273．

Dong L，Yang L M．Research on Low－frequency Anomalies of Microtremor Displacement Recorded by Digital Seismigraph before the Whenchuan Earthquake［J］．Northwestern Seismological Journal，2012，34（3）：268－273．（in Chinese）

［2］ 余怀忠，程佳，张小涛，等．多方法联合分析未来地震发生趋势［J］．西北地震学报，2012，34（1）：1－9．

Yu H Z，Chen J，Zhang X T．Multi－method Linked to Study Future Seismic Tendency［J］．Northwestern Seismological Journal，2012，34（1）：1－9．（in Chinese）

［3］ Sykes L R，Nishenko S P．Probabilities of Occurrence of Large plate Rupturing Earthquakes for the San Andeas，San Jacinto，and Imperial Faults［J］．J．G．R，1984，89：5905－5927．

［4］ K Mogi．Study of Elastcs Shocks Caused by the Fracture of Heterogeneous Materials and its Relation to Earthquake Phenomena［J］．Bulletin of Earthquake Research Institute，1962，40：125．

［5］ Kelleher J，Savino J．Distribution of Seismicity before Large Strike－slip and Thrust－type Earthquakes［J］．J．G．R，1975，80：260－271

［6］ Ellsworth W L，Lindh A G．，Prescott W H，et al．The 1906 San Francisco Earthquake and the Seismic Cycle，in Earthquake Prediction：An International Review．Eds．Simpson，D．W．，and Rechard［M］．Washington，D．C．：P．G．，AGU，1981：126－140

［7］ Ben－Zion Y，Sammis C G．Characterization of Fault Zones［J］．Pure Appl．Geophys．，2003，160：677－715．

［8］ Ben－Zion Y，Lyakhovsky V．Accelerated Seismic Release and Related Aspects of Seismicty Patterns on Earthquake Faults［J］．Pure Appl．Geophys．，2002，159：2385－2412．

［9］ Romachkova L L，Kossobokov V G，Panza G F，et al．Intermediate－term Predictions of Earthquakes in Italy，AlgorithmM8［J］．Pure Appl．Geophys．，1998，152：37－55．

［10］ Keilis－Borok V I，Shebalin P N．Special Issue－Dynamics of Lithosphere and Earthquake Prediction［J］．Phys．Earth．Planet．Inter．，1999，111：179－327．

［11］ Keilis－Borok V I，Ismail－Zadeh A，Kossobekov V，et al．Non－linear Dynamics of the Lithosphere and Intermediate－term Earthquake Prediction［J］．Tectonophysics，2001，338：247－260．

［12］ 刘蒲雄．大震前地震活动性的增强特征 ［J］．地震，1982，2：255－262．

Liu P X．The Enhancement Features of Seismic Activity before Large Earthquakes［J］．Earthquake，1982，2：255－262．（in Chinese）

［13］ Keilis－Borok V I，Soloviev A A．Nonlinear Dynamics of the Lithosphere and Earthquake Prediction［J］．Springer－Verlag，Heidelberg，2003，355：136－149．

［14］ Press F，Allen C．Pattern of Seismic Release in the Southern California Region［J］．J．Geophys．Res．，1995，100：6421－6430．

［15］ Bowman D D，Ouillon G，Sammis C G，et al．An Observation Test of the Critical Earthquake Concept［J］．J．Geophys．Res．，1998，103，24：359－372．

［16］ Yin X C，Chen X Z，Song Z P，et al．A New Approach to Earthquake Prediction－The Load／Unload Response Ratio（LURR）Theory［J］．Pure Appl．Geophys，1995，145：701－715．

［17］ Yin X C，Wang Y C，Peng K Y，et al．Development of a New Approach to Earthquake Prediction－Load／unload Response Ratio（LURR）Theory［J］．Pure Appl．Geophys．，2000，157：2365－2383．

［18］ Rundle J B，lein W，Tiampo K，et al．Linear pattern Dynamics in Nonlinear Threshold Systems［J］．Phys．Rev．，2000，E61：2418－2431．

［19］ Rundle J B，D L Turcotte，R Shcherbakov，et al．Statistical Physics Approach to Understanding the Multiscale Dynamics of Earthquake Fault Systems［J］．Rev．Geophys．，2003．41（4）：1019，DOI：10．1029／2003RG000135．

［20］ Tiampo K F，Rundle J B，McGinnis S A，et al．Pattern Dynamics and Forecast Methods in Seismically Active Regions［J］．Pure and Applied Geophysics，2002，159 （10）：2429－2467．

［21］ Bowman D D，King G C P．Accelerating Seismicity and Stress Accumulation before Large Earthquakes［J］．Geophys．Res．Lett．，2001，28（21）：4039－4042．

［22］ King G C P，Cocco M．Fault Interaction by Elastic Stress Changes：New Clues from Earthquake Sequences［J］．Adv．Geophys．，2001，44：1－38．

［23］ Yu H Z，Shen Z K，Zhu Q Y，et al．Increasing Critical Sensitivity of the Load／Unload Response Ratio before Large Earthquakes with Identified Stress Accumulation Pattern［J］．Tectonophysics，2006，428（1－4）：87－94．

［24］ Yin X C，Mora P，Peng K Y，et al．Load－Unload Response Ratio and Accelerating Moment／Energy Release Critical Region Scaling and Earthquake Prediction［J］．Pure Appl．Geophys．，2002，159：2511－2523．

［25］ Yin X C，Yu H Z，Kukshenko V，et al．Load－Unload Re－sponse Ratio（LURR），Accelerating Energy release（AER）and State Vector Evolution as Precursors to Failure of Rock Specimens［J］．Pure Appl．Geophys．，2004，161：2405－2436．

［26］ Yin X C，Zhang L P，Zhang H H，et al．LURR＇s Twenty Years and Its Perspective［J］．Pure Appl．Geophys．，2006，163：2317－2341．

［27］ 陈棋福，尹祥础，马丽．加卸载响应比的自然概率分布［J］．中国地震，1996，12（3）：270－273．

Chen Q F，Yin X C，Ma L．The Natural Probability Distribution of Load／unload Response Ratio［J］．Chinese Earthquake Research，1996，12（3）：270－273．（in Chinese）

［28］ 李佐唐．门源6．4级地前后加卸载响应比的异常变化［J］．西北地震学报，1997，18（4）：47－50．

Li Z T．Abnormal variation of the Load／unload Response Ratio before and after the MenyuanMS6．4Earthquake［J］．Northwestern Seismological Journal，1997，18（4）：47－50．（in Chinese）

［29］ 张昭栋，王秀芹，董守德．加卸载响应比在体应变固体潮中的应用［J］．地震，1999，19（3）：217－222．

Zhang S D，Wang X Q，Dong S D．Application of response ratio of Load and unload to Bulk strain earthtide［J］．Earthquake，1999，19（3）：217－222．（in Chinese）

［30］ 常克贵，高立新，张建业，等．加卸载响应比理论在包头西MS6．4地震预报中的应用 ［J］．西北地震学报，1999，21（4）：350－355．

Chang K，G，Gao L X，Zhang J Y．Application of the Loadunload Response Ratio Theory to Prediction the BaotouMS6．4Earthquake ［J］．Northwestern Seismological Journal，1999，21（4）：350－55．（in Chinese）

［31］ 任隽，陈运平，潘纪顺，等．海南岛及其近海中强地震前加卸载响应比的变化特征 ［J］．西北地震学报，2002，27（1）：71－4．

Ren J，Chen Y P，Pan J S，et al．Variational Characteristics of Load／Unload Response Ratio in Hainan Island and Its Adjacent Area before Moderate－strong Earthquakes［J］．Northwestern Seismological Journal，2002，27（1）：71－4．（in Chinese）

［32］ Cochran E S，Vidale J E，Tanaka S．Earthquake Tides can Trigger Shallow Thrust Fault Earthquakes［J］．Science，2004，306：164－166．

［33］ Tanaka S，Ohtake M，Sato H．Tidal triggering of Earthquakes in Japan Related to the Regional Tectonic Stress［J］．Earth Planets Space，2004，56（5）：511－515．

［34］ Jaume S C，Sykes L R．Evolution toward A Critical Point：A Review of Accelerating Seismic Moment／energy Release Prior to Large Great Earthquakes［J］．Pure．Appl．Geophys．，1999，155：279－06．

［35］ Bufe C G，D J Varnes．Predictive Modelling of the Seismic Cycle of the Greater San Francisco Bay Region［J］．J．Geophys．Res．，1993，98：9871－883．

［36］ Sammis C G，Smith S W．Seismic Cycles and the Evolution of stess Correlation in Cellular Automation Models of Finite Fault Networks［J］．Pure Appl．Geophys．，1999，155：307－34．

［37］ Reasenberg P A．Second－order Moment of Central California Seismicity 1969 －1982［J］．J．Geophys．Res．，1985，90：5479－495．

［38］ Keilis－Borok V I，L Knopoff．Bursts of Aftershock of Strong Earthquakes［J］．Nature，1980，283（P5744）：259－63．

［39］ 陈凌，刘杰，陈顒，等．地震活动性分析中余震的删除［J］．地球物理学报，1998，41（增刊）：244－52．

CHEN L，LIU J，CHEN Y，et al．Aftershock Deletion in Seismicity Analysis［J］．Chinese J．Geophys．，1998，41（S1）：244－52．（in Chinese）

［40］ Turcotte D L，W I，Newman，R Shcherbakov．Micro－and Macro－copic Models of Rock Fracture［J］．Geophys．J．Int．，2002，152：718－28．

［41］ Sornette D，C G Sammis．Complex Critical Exponents from Renormalization Group Theory of Earthquakes：Implications for Earthquake Predictions［J］．J．Phys．I．，1995，5：607－619．