高速列车气动噪声及影响
2013-09-04李人宪
袁 磊,李人宪
(西南交通大学 机械工程学院,四川 成都 610031)
0 引言
随着列车运行速度的提高,许多在低速时被忽略的问题都日渐突出,并且在很大程度上影响着列车的提速。车速提高,作用在列车车身的空气脉动压力波动也显著增加,气动噪声变得越来越明显。研究表明,高速列车气动噪声的大小主要取决于列车的运行速度v,气动噪声声压大约正比于v6~v8。因此,随着列车运行速度的提高,气动噪声将急剧增加。当列车的运行速度达到300km/h时,产生的气动噪声将超过轮轨噪声,成为高速列车的主要噪声源。所以,高速列车的气动噪声对环境有着不可忽视的影响,降低气动噪声已成为控制高速列车噪声的关键问题之一[1]。
本文采用计算流体力学流场大涡模拟方法结合Lighthill声类比理论,对高速列车外流场进行数值模拟计算,以得出车体表面气动偶极子声源分布情况,以此为声源边界条件,利用直接边界元法对声学方程进行求解,以对高速列车远场气动噪声的传播情况进行计算分析。
1 气动声学理论
1952年,Lighthill在没作任何简化和假定的前提下,通过流体运动方程,得到自由空间中流场声波运动与流场参数之间关系的Lighthill波动方程:

其中:Tij为Lighthill张量;ρ为流场密度;ρ′为流场密度脉动量,ρ′=ρ-ρ0,ρ0为未受扰动时流场密度或其均值;▽为 Hamilton算子;vi、vj分别为i、j方向流体速度分量;δij为流体张量;pij=(p-p0)δij-σij,σij为流体的黏性应力张量,p为流场压力,p0为未受扰动时流场压力或其均值;c0为声音在匀质介质中的传播速度。
方程(1)将流场参数与声场参数分立于方程的两侧,为流场和声场的解耦分析建立了基础。1955年,Curle将Lighthill方程进行推广,得到考虑流场中存在固壁边界影响的更一般的方程的解,即Lighthill-Curle解形式。1966年,Ffowcs Williams和 Hawkings将Curle的研究成果扩展到运动固体边界,并按Lighthill方程的推导方法,得出FW-H方程:
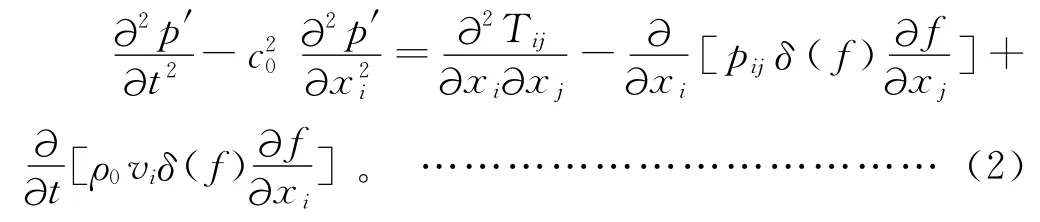
其中:p′为流场压力脉动量,p′=p-p0;δ(f)为狄拉克函数;函数f用来描述无限空间中的外部流场问题。
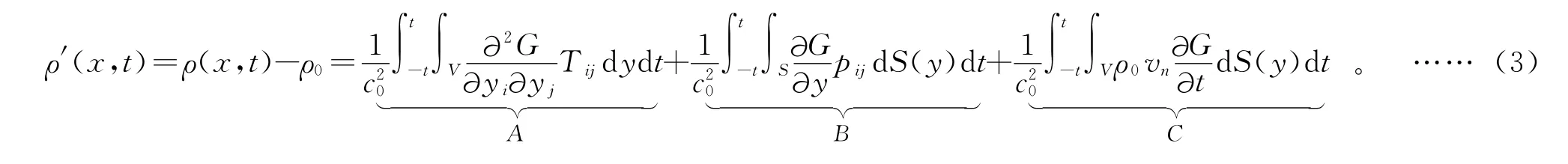
1974年,Goldstein拓展了FW-H方程,得到了流场发声声源更清晰的解形式[2]:其中:函数G为格林函数;vn为垂直于表面方向上的速度分量;ρ(x,t)为点x处t时刻的密度;ρ′(x,t)为点x在t时刻的密度脉动量;V、S分别为体积分、面积分。
式(3)中,等式右边A项为存在于运动固体表面之外的四极子声源项;B项为由固体表面气体脉动压力引起的偶极子声源项;C项为由固体表面垂直运动引起的单极子声源项。
单极子声源强度与车体表面垂向速度有关,而车体表面可近似看作是刚性的,垂向运动速度几乎为零,故单极子声源的影响可忽略不计。四极子声源强度与偶极子声源强度之比正比于马赫数的平方,本文研究车速为300km/h,此时的偶极子声源强度远强于四极子声源,故四极子声源也可以忽略。
2 车体表面偶极子声源
偶极子声源的计算需求解列车在一定速度下运行时其周围的流场参数,得出车体附近气体脉动压力,再通过傅立叶变换得到不同频域下的列车表面偶极子声源强度[3-6]。由于声学计算的精度要求边界网格大小不得超过最小计算波长的1/6,针对人耳对1kHz~3 kHz的频率范围声音最为灵敏并考虑到目前计算机的计算能力,本文分析最高频率为2 000Hz,并取头车和尾车建立计算模型,如图1所示。

图1 CRH2型高速列车几何模型
采用大涡模拟湍流模型,对时速为300km/h的列车外部非定常流场进行仿真计算。将流场动态计算结果转换成车体表面偶极子声源强度分布,如图2所示。从图2可见,最大声压级(105dB)出现在头车底部转向架附近;车头与车身过渡曲面区域和车身中段的气流分离附着区湍流强度较大,其声源声压级也较大,为69dB~89dB。在速度相同的条件下,其他频率车身表面偶极子声源的分布规律也基本一致,但随着频率的升高声源声压级有所下降。

图2 车身表面偶极子声源分布(1 000Hz,300km/h)
3 列车声源辐射场及周边环境噪声分析
将空气密度设定为1.225kg/m3,声速为340m/s,在300km/h速度下高速列车表面分布的偶极子声源作为边界条件,利用直接边界元,计算出列车外部辐射声场的声压级分布情况。列车纵向对称面上1 000 Hz和2 000Hz的声压分布情况如图3所示。从图3中可以看出:①车体表面偶极子声源在纵向对称面上辐射主要在与对称面成20°~160°夹角区间内;②频率越低,纵向对称面上声源辐射方向与地面夹角越大,声压越高。

图3 列车周边噪声辐射声级场
国标规定我国铁路边界(距铁路外侧轨道中心线30m处)噪声限值为70dB(A),其测点位于距铁路外侧轨道中心线30m 处,高1.2m[7]。在300km/h的时速下,离铁路中心线不同距离高1.2m处每隔2m取1个测点,共35个测点,在不同频率下的最大A计权声压分布见表1。

表1 距轨道中心不同距离最大声压分布数据 dB(A)
由表1可见:同一频率下,随着离轨道中心距离的增加,最大声压值降低,频率越高,声压衰减越明显;不同频率下,距离中心线相同距离的噪声声压也不相同,频率越高声压越低;在国标规定测点处,最高A计权声压出现在500Hz频率下,为70.18dB,超过国标限值,因此控制铁路沿线气动噪声十分必要。
4 声屏障对列车气动噪声外辐射场影响分析
距离轨道中心线5m处有、无声屏障时列车头部横断面辐射声场如图4~图6所示。对比可知:①添加声屏障之后,最大声压值都有所升高,增加范围在2 dB~5dB,屏障内侧车身周围声压值都有所上升;②声屏障对低频噪声传播规律影响不是很明显;③添加声屏障之后噪声沿屏障顶部向外辐射,导致屏障外侧近地面声压降低,其中5 00Hz~1 000Hz噪声受阻最为明显。
为研究声屏障对铁路沿线气动噪声的影响,本文着重分析不同频率下铁路边界气动噪声分布情况。为降低死点对结果的影响,对铁路边界沿线70m范围内的35个测点的声压取平均值得到平均声压及最大声压,见表2。
由表2可见:添加声屏障后,沿线声压在100Hz~2 000Hz都有所下降,平均声压降低在3dB~12dB,其中,500Hz~1 500Hz频率段声压降低最为明显,在1 000Hz声压降低最大,最高声压降低11dB;在添加声屏障后,100Hz时隔音效果不明显,最高声压为77.09dB,也超过了国标限值。

图4 500Hz时车头横断面上噪声辐射声级场
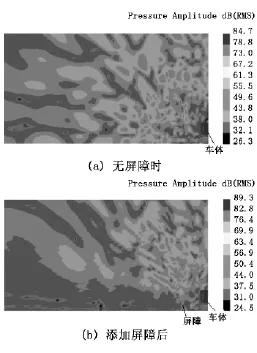
图5 1 000Hz时车头横断面上噪声辐射声级场
5 结论
从Lighthill声类比理论出发,采用计算流体力学与边界元相结合的计算方法,对列车外部气动噪声场的辐射声压分布规律以及声屏障对其辐射规律的影响进行了分析。分析结果表明:
(1)列车高速运行时,表面产生的偶极子声源主要集中在湍流强度较大部位,因此,降低列车运行时表面湍流强度能够在根源上减少气动噪声的产生。
(2)铁路周边距离轨道中心线越远,最大声压值越低,频率越高,衰减越明显;当列车在时速300km/h运行时,在铁路边界500Hz频率气动噪声已达到70.18dB,超过国标限值70dB,频率越低,最高声压值越高;气动噪声将对铁路周边环境产生较大影响,控制高速铁路气动噪声对周边环境影响很有必要。

图6 2 000Hz时车头横断面上噪声辐射声级场

表2 铁路边界测点在有、无声屏障时不同频率下的声压
(3)声屏障对低频噪声的传播路径影响不大,低频噪声更容易绕射。
(4)声屏障能使铁路边界100Hz到2 000Hz的气动噪声声压降低3dB~12dB,最高声压能够降低11dB左右,在一定程度上降低了气动噪声对铁路沿线的影响。
(5)声屏障在降低铁路沿线噪声的同时也会使得屏障与列车之间的噪声值上升,这可能使列车内噪增加,车内舒适度下降。
[1] Talotte C.Aerodynamie noise:a cirtieal survey[J].Journal of Sound and Vibration,2000,231;549-562.
[2] Goldstein M E.Aeroacoustics[M].New york:McGraw-Hill International Book Company,1976.
[3] 李增刚.SYSNOISE Rev5.6详解[M].北京:国防工业出版社,2005.
[4] 郑拯宇,李人宪.高速流线型车辆稳态下速度风噪声源数值分析[J].重庆工学院学报(自然科学版),2009,23(6):1-4.
[5] 夏恒,宫镇.关于高速车辆内部气流噪声计算方法的研究[J].汽车工程,2003,25(1).79-81.
[6] 郑拯宇,李人宪.高速车辆外部气动噪声场数值模拟研究[D].成都:西南交通大学,2010:24-59.
[7] 国家环境保护局.GB12525—90铁路边界噪声限值标准及其测量方法[S].北京:中国标准出版社,2008:1-5.
