基于多通道Gabor滤波和2DPCA的虹膜识别算法

何 威，周 克

(贵州大学电气工程学院，贵州贵阳550025)

0 引言

近年来，作为多模态生物特征识别技术之一的虹膜识别［1］技术因其高识别率与稳定性等特点受到了计算机视觉研究领域的广泛青睐。生物虹膜同其他生物特征，如指纹、掌纹、声音、步态等相比具有唯一性、独特性和高稳定性的特点。结构复杂的虹膜纹理蕴藏着大量的生物特征信息［2］，关于虹膜特征提取的算法主要分为拉普拉斯金字塔算法、小波变换过零检测法、多通道Gabor滤波法、Haar小波分解法、神经网络分类器法和局部过零检测法等。目前虹膜特征提取技术的主流是多通道Gabor［3-4］滤波算法，该算法能从方位和频率两方面来有效地描述个体虹膜所特有的纹理特征，提取得到的虹膜特征信息量大、精度高。Gabor特征矩阵是虹膜图像与多通道Gabor滤波器的卷积，维数通常很高，这些高维特征向量既影响虹膜匹配的运算速率，又易造成小量纹理信息丢失，因而需要对其进行降维。主分量分析(PCA)［4-6］是基于子空间投影的降维方法，它能够有效地去除样本向量中各元素的相关性，把信息尽量集中到少量主分量中，从而有效地对样本进行降维和主特征提取。但是PCA需要在特征提取之前将二维图像矩阵转换为一维列向量，这个转换虽然降低了图像维数，但其协方差矩阵会产生维数激增。2DPCA［5-9］与PCA不同，它能够直接针对二维图像来构造协方差矩阵，不需要预先把矩阵按列展开成一维向量，在很大程度上降低了协方差矩阵的维数，从而降低了运算难度，提高了特征匹配的特征精度和运算速率。

本文提出了基于多通道Gabor滤波和2DPCA的虹膜识别算法，首先对经预处理后得到的矩形图形进行16通道的Gabor滤波，以16通道滤波子图像的关键点与其中心坐标之间的相对距离作为矩阵子元素来构造特征矩阵，然后通过2DPCA算法对得到的特征矩阵进行降维处理，形成特征向量。最后，利用差异度匹配法完成虹膜识别。由于算法中多通道Gabor滤波器使用了多尺度纹理分析算法来提取虹膜纹理特征，对光照的变化不敏感，在一定程度上克服了虹膜采集过程中光照对虹膜纹理的影响。

1 多通道Gabor滤波器分析

Gabor函数可以通过旋转、缩放和平移形成一组自相似的小波族和丰富的多通道滤波器族。多通道二维Gabor滤波器的数学原型为

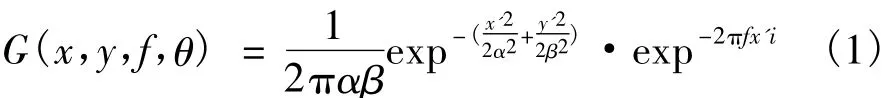
式中:f为滤波器的中心频率;θ为滤波器的方向;α为高斯函数的宽度;β为高斯函数的高度;(x'，y')为旋转θ后的坐标系，

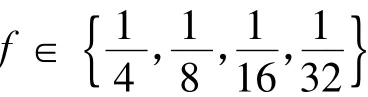
和4 个滤波方向 θ∈{0°，45°，90°，135°}，形成16 通道的Gabor滤波器组，每个滤波通道都由奇、偶2个滤波器构成，总共32个滤波器。考虑到虹膜纹理的独特性质，定义滤波器组的波长分别为4、8、16、32像素。令高斯函数的宽度α与高度β相等并分别为4、8、16、32。由于滤波器组的波长为2时其虚部在离散情况下会出现欠采样［10］现象，而且在高频通道上会引入更多的噪声，故不采用此波段。16通道Gabor滤波器组的工作框图如图1所示。

为了提取虹膜图像在不同尺度和不同方向上的纹理特征，定义了一组多通道Gabor滤波器。设定4个中心频率

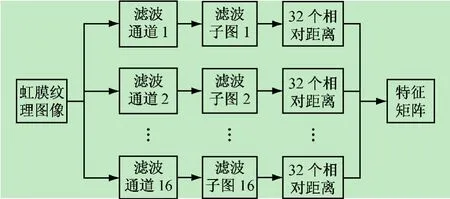
图1 16通道Gabor滤波器组的工作框图

2 特征提取及降维处理

2.1 特征提取

在一幅滤波图像矩阵中，最大系数绝对值对应的点和所使用的滤波器的特征往往是最相近的，这些点可看作是当前滤波通道的特征点。由于在虹膜采集过程中会受到来自光照强度、眼睫毛、环境噪声以及其他因素的影响，滤波子图像中会存在很多具有相似系数值的“伪特征点”，选取一个具有最大系数绝对值的特征点是缺乏说服力的。从维数为32×32的滤波子图中选出一定数量的特征点，其重心称为关键点［11］，它模拟了滤波通道的特征，与理想特征点具有最大似然度。

假设F(x，y)是滤波后某一子图像的绝对值，则

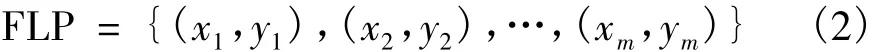
表示一系列特征点的坐标，m为一参数，其重心坐标(xKP，yKP)即该滤波通道的关键点。重心坐标(xKP，yKP)的表达式如下:

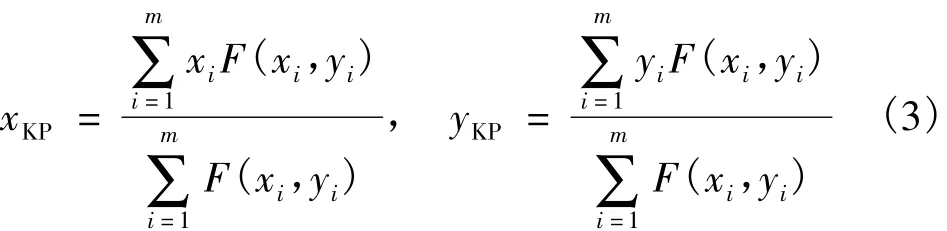
式中，(xi，yi)∈FLP。

图1中每幅滤波子图都可得到32个关键点:

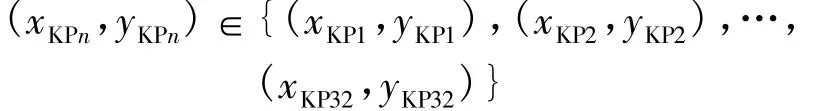
为了组成特征矩阵［12］，还需定位出每幅子图中关键点的中心Oj，其坐标(Oj(x)，Oj(y))的计算表达式如下:

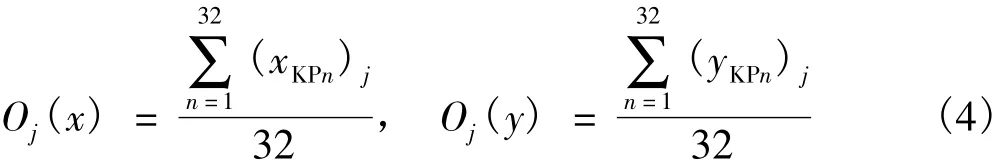
式中，j=1，2，…，16。中心坐标(Oj(x)，Oj(y))和关键点(xKPn，yKPn)之间的相对距离［13］Dj(n)被称为特征值，它代表了虹膜复杂的纹理信息，

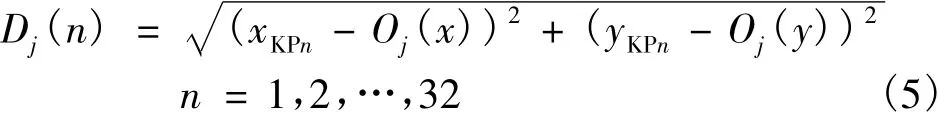
一幅虹膜图像通过16通道的Gabor滤波器后得到了16幅子图，每一幅滤波子图又可得到32个相对距离，那么特征矩阵M便可由每幅虹膜图像得到的512个相对距离组成，如下式所示:

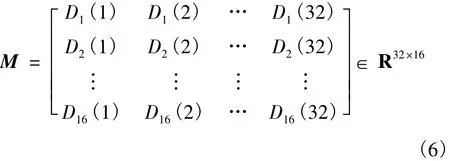
2.2 PCA与2DPCA降维

主分量分析是一种基于统计特性的图像分析方法，假定有P个统计相关的性质指标集合{x1，x2，…，xP}，由于它们之间的相关性，在这P个性质指标中存在信息的冗余。现在希望通过正交变换，从中获得K个新特性集合{，，…，}。这些新特征由于彼此正交，它们之间不再有信息的冗余。具有较大能量的K(K＜P)个性质指标可以视为P个原始性质指标的主要成分，简称主分量。利用主分量进行的数据或者信号分析称为主分量分析(PCA)。将PCA运用到图像处理当中，能够充分去除图像的相关性，把有用的信息集中到数目尽可能少的主分量中。利用PCA法对图像进行分析时，需要将一幅分辨率为m×n的图像展开成一个大小为1×m×n的列向量，进而构造图像的协方差矩阵。设样本集 x有 m×n个样本，xi∈Rmn×1(i=1，2，…，m ×n)表示第 i个样本形成的向量，那么该样本集的协方差［6］矩阵A可以表示为

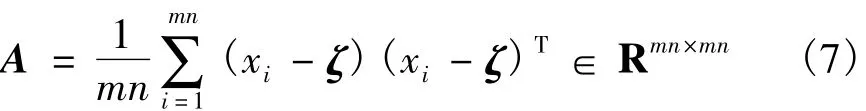
式中，ζ为样本集的平均向量，即

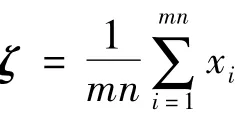
从式(7)可以看出，经过PCA 处理后，图像协方差的维数会激增至mn×mn，造成“维数危机”，整个特征抽取过程所耗费的计算量相当大，提取速度慢。

2DPCA可直接对原始二维图像矩阵进行主分量分析，不需要将其转换为一维列向量，有效地降低了协方差矩阵的维数。这种统计方法计算简便，对图像纹理的特征提取更加直观，因此在计算机视觉和模式识别研究领域中得到了广泛运用。以容量为T的虹膜图库作为研究对象，设样本 Xj∈{X1，X2，…，XT}(j=1，2，…，T)。在此图库中，每幅虹膜样本的分辨率均为m×n，图像样本集的均值为x珋，则该虹膜样本集的协方差矩阵为

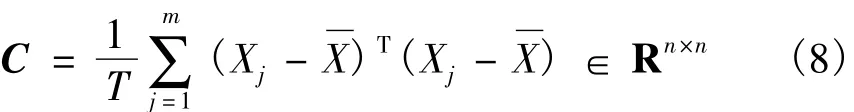
从式(8)可以看出，协方差矩阵C的维数已降至n×n，远小于PCA法的mn×mn，在很大程度上降低了特征抽取的数据运算量。而且C的维数与所研究的虹膜图库的容量无关。因此，2DPCA法在计算速度和运算精度上都优于PCA法，适合对多通道Gabor滤波器输出的特征矩阵进行降维。

3 虹膜识别

两幅虹膜图像特征向量之间欧氏距离的差值可以表征两幅虹膜图像的差异度。提取到虹膜纹理的特征向量之后，本文采用差异度法来完成特征匹配。差异度法即把计算得到的差异度数值和实验中统计得到的差异度限值进行比较来判断所选取的两幅虹膜是否匹配，从而识别个体身份。

定义M1和M2分别为两幅虹膜图像的特征矩阵，经式(8)处理后，其协方差矩阵分别为CM1和CM2，如下式所示:

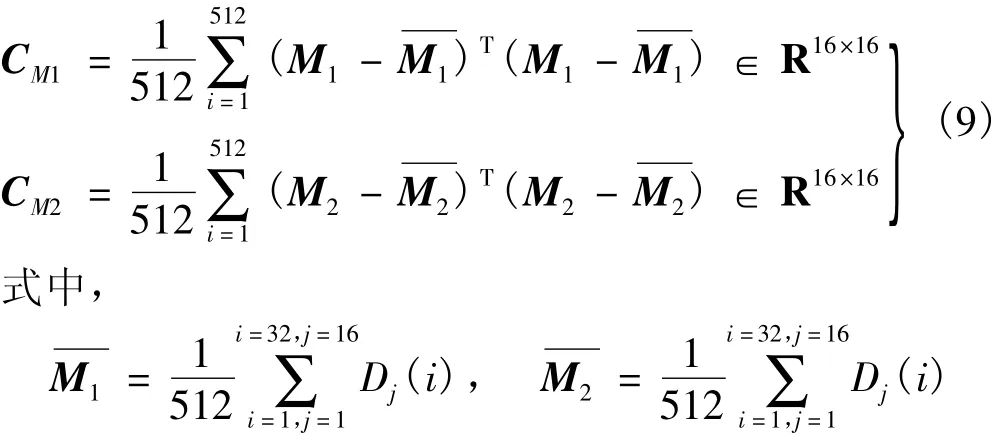
由式(9)可知，协方差矩阵CM1和CM2的维数是由多通道Gabor滤波器的通道个数来决定的。由于本算法采用了16个滤波通道，所以CM1和CM2的维数均为16×16。

将C里的特征值λ按照从大到小的顺序进行排列，就可以得到维数为1×256的特征行向量［14］λ(i)，如下式所示:

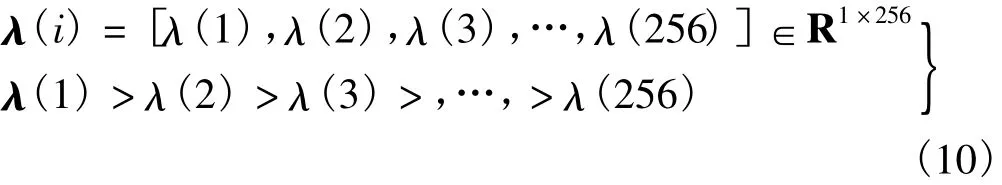
经过特征提取和降维处理，两幅虹膜图像I1(x，y)和I2(x，y)最终可分别对应2个特征行向量，记为λ1(i)与λ2(i)，那么这两幅虹膜图像之间的差异度Diff定义为

通过式(11)计算得到的差异度Diff数值越小，表明参与匹配的两幅虹膜图像越相似。设定一个固定上限值ρ，通过比较差异度数值Diff与ρ的大小来判断参与识别的两幅虹膜图像是否匹配。由于ρ值的设定与参与识别的虹膜图库的容量有关，并非一个定值，它的大小会随着图库中虹膜数量的多少而发生变化，具有即时更新的特点，因而对具有各类容量的虹膜识别系统均具有良好的适应能力。

4 实验结果及分析

4.1 实验仿真及结果

本文采用CASIA1.0版的虹膜数据库，从108个人的虹膜图库中随机选取25个人(每人2张)的人眼图像作为样本进行匹配识别。参与识别的虹膜图像分辨率为320×280，如图2(a)所示。运用文献［15-16］提到的预处理方法，裁剪出虹膜圆环区域，如图2(b)所示;归一化及增强后的虹膜分别如图2(c)、2(d)所示。

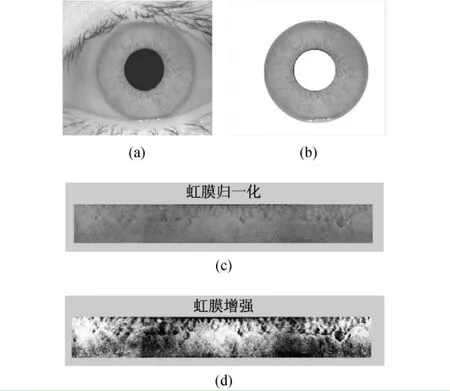
图2 虹膜预处理

对于一个虹膜识别系统，用识别率ε、拒识率σ和误识率δ这3个指标来表征系统性能:

其中，识别率+拒识率+误识率=100% 。

实验中，首先对参与识别的50幅虹膜图像进行预处理，然后将经归一化及增强处理后的虹膜图像通过16通道的Gabor滤波器，以获得特征矩阵M，对M经2DPCA算法降维处理后得到协方差矩阵C，然后对C里面的特征值进行降序排列，最后结合差异度匹配法完成虹膜识别。如果随机选取的两幅虹膜图像之间差异度数值Diff≤ρ，虹膜识别系统会提示匹配成功并开放来访者的访问权限;如果Diff＞ρ，系统则提示匹配失败并提示来访者重新识别。实验中经过反复计算与统计，得到了虹膜图库容量为108人时的差异度限值ρ=15.238。

从50幅虹膜图像中随机选取样本数分别为5、15和35的样本虹膜作为训练样本，其余样本作为测试样本。以对特征矩阵M不做任何降维处理的方法记为方法1，对M仅做PCA变换的方法记为方法2，本文的方法记为方法3。对以上3种方法在训练样本数分别为5、15和35情况下的匹配耗时进行分别统计，如表1所示。

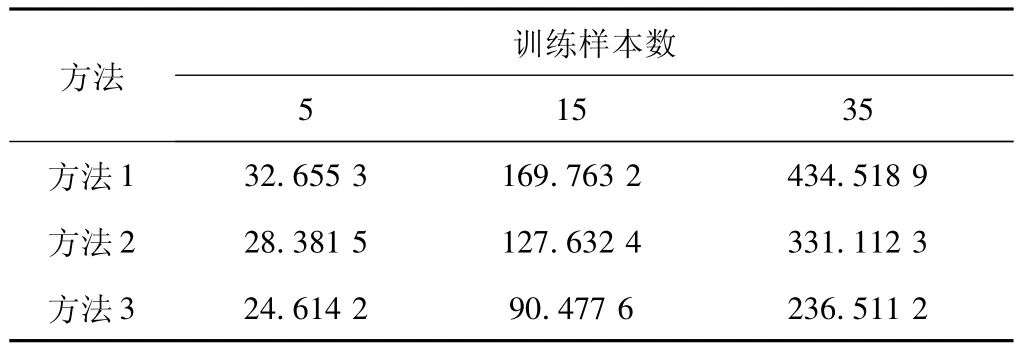
表1 3种方法对应的匹配耗时 s

此外，本次实验对3种方法在不同训练样本数下的系统识别率也进行了统计和比较，如图3所示。

图3 3种方法在不同训练样本数下的系统识别率

4.2 实验分析

参与识别的50幅虹膜图像中，有6幅虹膜受到眼睫毛和眼睑的严重干扰，导致虹膜圆环有效面积变小，经预处理后，虹膜纹理信息严重丢失，影响了系统识别率。由于在虹膜采集过程中已经删减了质量低下的虹膜图像，所以本次实验中，系统的拒识率为0。由图3可以观察到，当虹膜样本数为5时，3种方法的识别率均达到了100%。随着训练样本数的增加，系统识别率稍有下降，但从统计的实验数据来看，方法3的最低识别率为88%，仍高于方法1与方法2。方法1、2的识别率相差不大，曲线贴合度高。就识别速度上看，方法1的匹配耗时明显长于方法2、3。在相同的实验环境下，本文提出的方法的识别时间约为方法1的一半，而且随着样本数目的增加，3种方法之间的耗时之差会愈加增大。由此观之，本文提出的方法不仅具有较高的识别率，而且系统识别速度更快。

5 结语

本文将16通道的Gabor滤波器应用于虹膜纹理信息的提取过程，运用2DPCA技术对多通道Gabor滤波器输出的特征矩阵进行降维，结合差异度匹配法完成了系统的整个识别过程。实验结果表明，与未进行降维处理的方法和仅作PCA变换的方法相比，本文提出的算法既能消除“维数危机”，降低匹配耗时，提高系统的识别时效性，又能在一定程度上提高虹膜识别率，并且具有良好的图库容量适应性，能应用于对识别率和时效性要求较高的门禁系统或公司考勤系统。

［1］ Chomtip P，Bundit S，Yutika J，et al.2010 international conference on test and measurement［D］.Thailand:Mahidol University，2010:68-71.

［2］ 苑玮琦，赵彦明，张志佳.基于能量最大响应方向的虹膜识别算法［J］.计算机应用研究，2010，27(5):1977-1980.

［3］ 吕林涛，杨 涛.一种基于奇对称2DLog-Gabor的虹膜特征提取算法［J］.计算机应用，2009，29(4):976-978.

［4］ 王相海.基于PCA与LDA的虹膜识别研究［D］.沈阳:辽宁师范大学，2009.

［5］ 李建华.基于增强2DPCA+PCA的人脸识别系统［D］.太原:太原科技大学，2010.

［6］ 苏 滨，姜 威.一种基于Gabor小波和2DPCA的掌纹识别改进算法［J］.计算机应用与软件，2011，28(1):242-245.

［7］ 董钦科，王相海.基于多频带2D_PCA的虹膜识别算法［J］.计算机科学，2009，10(36):280-283.

［8］ 陈伏兵，陈秀宏，张生亮，等.基于模块2DPCA的人脸识别方法［J］.中国图像图形学报，2006，11(4):580-585.

［9］ 陈春兰，曾黄麟.一种基于2DPCA的人可识别方法［J］.现代电子技术，2008(20):151-152.

［10］ 苑玮琦，刘汪澜，柯 丽，等.用于虹膜特征提取的Gabor滤波器参数选取方法的研究［J］.光电子·激光，2008，19(9):1235-1239.

［11］ 杨昌盛.虹膜图像预处理及关键点提取方法的研究［D］.长沙:中南大学，2009.

［12］ 于 力.虹膜图像的特征分析研究［D］.哈尔滨:哈尔滨工业大学，2006.

［13］ YUAN M L，ONG S K，NEE A Y C.Registration using natural features for augmented reality systems［J］.IEEE Trans on Visualization and Computer Graphics，2006，4(12):569-580.

［14］ YUAN XIAO-YAN，ZHOU HAO，SHI PENG-FEI.Iris recognition:a biometric method after refractive surgery［J］.Journal of Zhejiang University Science A，2007，8(8):1227-1231.

［15］ 常海军.虹膜识别算法研究与实现［D］.杭州:浙江大学，2005.

［16］ 黄 祎.虹膜识别的预处理算法研究［D］.成都:电子科技大学，2008.