Mathematica软件绘制函数图像的纠偏与优化

王 彬，徐 明

（泰州师范高等专科学校，江苏 泰州 225300）

函数图像的绘制在研究函数的性态、求方程的近似解等方面具有重要的作用，因此，准确地描绘出函数的图像，是学习与应用高等数学的重要内容。随着软件技术的不断发展，许多数学软件给出了较多的函数图像绘制方案，只要输入比较简单的绘图命令，就可轻松作出函数图像。如，由沃尔夫勒姆研究公司（Wolfram Research Inc.）研发的Mathematica软件，给出了下列基本的绘图命令：

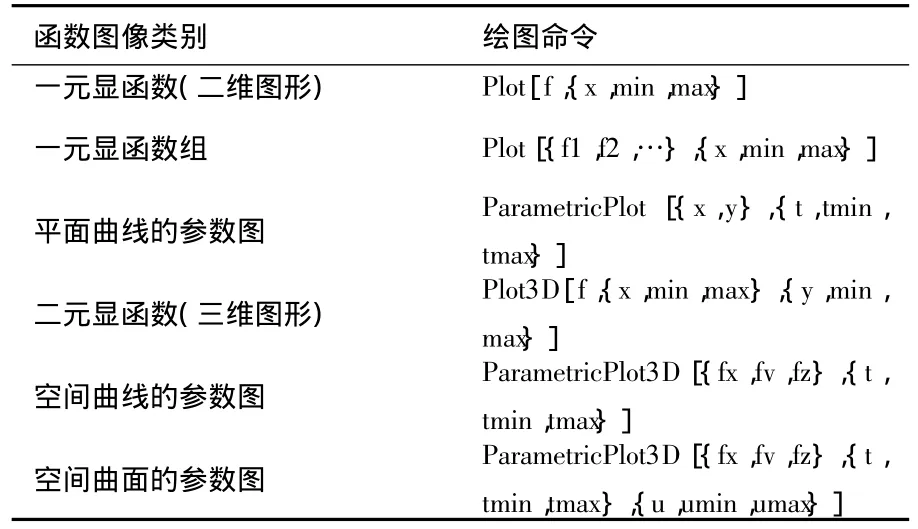
函数图像类别 绘图命令一元显函数（二维图形） Plot［f，{x，min，max }］一元显函数组 Plot［{f1，f2，…}，{x，min，max}］平面曲线的参数图 ParametricPlot［{x，y}，{t，tmin，tmax}］二元显函数（三维图形） Plot3D［f，{x，min，max}，{y，min，max}］空间曲线的参数图 ParametricPlot3D［{fx，fv，fz}，{t，tmin，tmax}］空间曲面的参数图 ParametricPlot3D［{fx，fv，fz}，{t，tmin，tmax}，{u，umin，umax }］

然而，由于系统的默认效果与通常的函数图像表示形式有一定差距，从而在视觉上影响了函数图像的准确度，以及位置特征的判定等。利用Mathematica软件强大的人机互动功能，结合极限、导数等对函数图像特征的判定，调用系统内置函数，可以较好地解决以上问题。

一、函数图像的纠偏

Mathematica在画函数f的图像时，为了得到光滑的曲线，系统需要计算许多点的函数值。系统“Plot”命令中，必须给出自变量的取值范围，并默认横轴与纵轴比为黄金分割，系统根据自变量的取值情况自动计算出函数的值域，从而作出函数的图像。

如要描绘一元函数f（x）的图像，只要输入命令Plot［f（x），{x，min，max}］，同时按“Shife+Enter”，系统则自动显示函数图像。

In［1］：=Plot［1+36x/（x+3）^2，{x，－6，6}］

Out［1］=Graphics

In［2］：=Plot［1+36x/（x+3）^2，{x，－60，60}］

Out［2］=Graphics

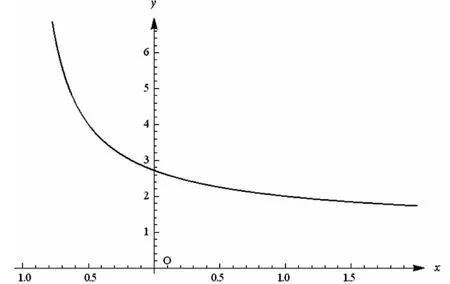
In［3］：=Plot［（1+x）^（1/x），{x，－1，2}］

Out［3］=Graphics

其实这是因为系统自动调整了坐标轴的位置，其坐标原点并不是（0，0），函数图像并没有失真，只是视觉上与通常函数图像表现方式不一样。对于这一问题，采用上例的方法调整x的取值范围，可以适当改变视觉效果，但难以解决坐标原点不在（0，0）点的问题，这就需要对函数图像进行优化。

二、函数图像的优化

Mathematica绘图时允许用户设置选项值对绘制图形的细节提出各种要求。例如，要求取消坐标轴，给图形加框线等。每个选项都有一个确定的名称，以“选项名－＞选项值”的形式放在Plot中最右边位置，一次可设置多个选项，选项依次排列，以逗号相隔，若不设置选项，系统取各选项的默认值。

Mathematica对函数图像进行修饰的选项主要分为两大类：第一类选项的主要功能是修饰曲线的样式，用来控制图形的生成过程、控制图形元素的构造，这是比较重要的一类选项，其选项名只有一个PlotStyle；第二类选项的主要功能是修饰图形或坐标轴的外观，可以通过选项改变图形的显示比例、为图形加背景、加网格、控制作图的区域及图形是否显示，以及是否显示坐标轴，坐标原点的位置，坐标轴上的刻度等。

以上选项名称、功能及使用方法都可通过《Mathematica教程》或Mathematica软件的帮助查阅。这里主要通过修饰坐标轴的外观举例说明如何对函数图像优化。修饰坐标轴外观的常用选项如下表：

选项名 取值范围 默认值 功能Axes True/False True 是否画坐标轴AxesOrigin Automatic/{x，y} Automatic 坐标原点AxesLabel None/{“字符串1”，“字符串2”} None 给坐标轴标注Frame True/False False 图形是否加框Ticks Automatic/{x，y}/{x1，y1，…}，{x2，y2，…} Automatic 坐标轴刻度Epilog None/{Text［“O”，{x，y}］}None 是否标注原点

＞{0，0}，AxesStyle－＞Arrowheads［0.03］，Epilog－＞Text［“O”，{0.1，0.

2}］，AxesLabel－＞{x，y}］

Out［4］=Graphics

例4作出x2+y2+z2=1的图像

Mathematica关于二元函数（三维图形）的作图命令中，默认效果是加立体框的，坐标轴位置位于立体框上，且为了更好地显示立体效果，系统对图像自动添加网络线，并根据透视情况着色。因此在实际操作中，可以对相关选项进行设置，以达到预期效果，本例仅就去外框与调整坐标原点的位置进行演示。

In［5］：=ParametricPlot3D［{Cos［u］Sin［v］，Cos［u］Cos［v］，Sin［u］}，{u，0，2Pi}，{v，0，2Pi}，Boxed －＞False，AxesOrigin－＞{0，0，0}］

Out［5］=Graphics3D（略）

系统推荐的二元函数（三维图形）的作图命令主要有显函数作图与参数方程作图，本例隐函数的图像是通过参数方程作图命令实现的。

三、函数图像的动画

为了更好地研究含参数函数的变化规律，可以借助Mathematica软件中的交互式操控函数制作函数的动画，这里仅就可以直接访问广大功能强大的互动函数“Manipulate”的操作举例说明。

例5［2］作出函数y=sin（ax+b）的图像，观察图像随a，b的变化情况

In［6］：=Manipulate［Plot［Sin［ax+b］，{x，0，2Pi}］，{a，1，4}，{b，0，10}］

Out［6］=Graphics

点击a，b滑动条右边的“+”可出现如录音机上面的按钮（如图所示）。

点击a或b的播放按钮或拖动滑动条，可以得到y=sin（ax+b）随a，b变化的动画效果，限于篇幅，这里不再演示。

利用函数图像的动画效果，可以很好地演示极限变化过程，以及定积分定义中分割、求和、近似计算的直观效果。