关于信号与系统中信号运算的研究

杨立娟，梁 娟，李冬芬

（福建农林大学 东方学院，福建 福州 350017）

在信号与系统中，当信号进行传输时，由于远距离或者系统自身的因素，往往会造成所接收到的信号相对于原信号而言，存在着时延或翻转等现象。例如，在雷达系统中，信号处理是一项关键技术［1］，由于雷达信号通常是远距离发送和接收，因此在信号处理过程中，要注意多径传输存在的时延问题［2］。在通信系统中，长距离传输电话信号时，可能会听到回波，这是幅度衰减的语音信号［3］。此外，信号的反褶、压缩和扩展也是常见的运算。而在实际生活中，一个信号在传输过程中，由于各种原因，通常不止包括一种基本运算，而是综合了移位，反褶以及尺度倍乘等两种或两种以上的运算。由于包含了多种运算，在信号的处理过程中，很容易出现在移位方向和移位单位上的错误，以及信号是压缩还是扩展等问题。

针对上述情况，本文建立在信号的基本运算基础上，通过探讨移位，反褶和尺度倍乘的综合运算，对在运算过程中容易出现的移位问题作了详细的研究和说明。

一、信号的基本运算

信号的基本运算包括信号的移位、反褶、尺度变换、微分和积分等，其中以移位、反褶以及尺度变换运算最为常见，在这三种运算中，又以移位运算最为关键，下面依次介绍这三种运算。

1.信号移位运算

将f（t）表达式的自变量t更 换（t+t0）（t?0为正或负实数），则?f（ t+t0）相当于f（t）波形在t轴上的整体移动。当t0＞0时，相当于f（t）波形在t轴上向左移动；当t0＜0时，相当于f（t）波形在t轴 上向右移动。如图1.1所示。

图1.1 信号的移位运算

2.信号反褶运算

将信号f（t）（或f（k））的自变量t（ 或k）换成－t（ 或－k） ，得到另一个信号f（－t）（或f（－k）），则称这种变换为信号的翻转运算。如图1.2所示。

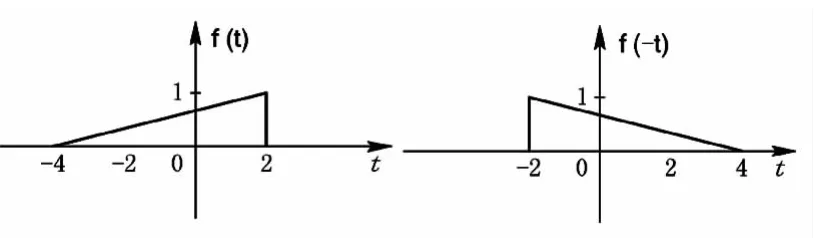
图1.2 信号的翻转运算

3.信号尺度变换运算

将信号f（t）的自变量t乘以正实系数a， 则f（at）称为时间轴的尺度倍乘或展缩。其中，a＞1表示压缩，0＜a＜1表示扩展，如图1.3所示。

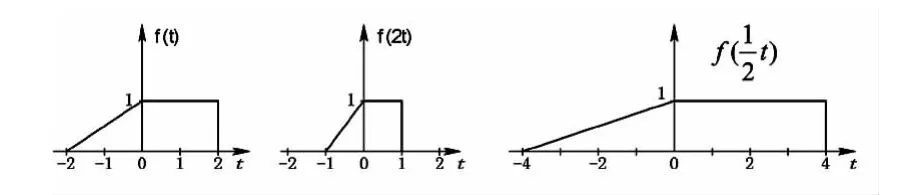
图1.3 信号的移位运算

综上，我们可以看出，如果对一个函数f（t）进行单一的运算，其方法和过程都较为简单。但是，在信号处理过程中，往往不仅仅是对信号进行移位或反褶等单一的运算，实际上，它伴随着两种或两种以上的综合运算，由于这种运算是信号处理过程中最常见的运算，因此，有必要对其进行详细的研究。

二、信号的综合运算

在第2小节，已经对信号的基本运算进行了详细的说明，接下来，我们来讨论当自变量t更换为（at+t0）时信号f（at+?t0）的运算。

若f（t）的自变量t更换为（at+t0）（其中a，t0是给定的实数），此时，f（at+t0）相对于f（t）可以是扩展（|a|＜1）或压缩（|a|＞1），也可能出现时间上的反褶（a＜0）或移位，而整体的波形仍保持与f（t）相似的形状。在这个综合运算过程中，无论是对f（t）先进行移位，还是先反褶，或是先尺度倍乘，三种方法最终得到的波形是一样的。通过研究证明，无论是哪一种方法，在移位运算过程最容易出现错误。针对以上观点，以移位运算为主要研究对象，结合实例来分析错误的原因以及应注意的问题。

已知信号f（t）的波形如图2.1所示，如果将自变量t更换为（1－2t），那么函数f（1－2t）的波形可以将f（t）的波形按先尺度变换，再移位，最后反褶的顺序来得到。

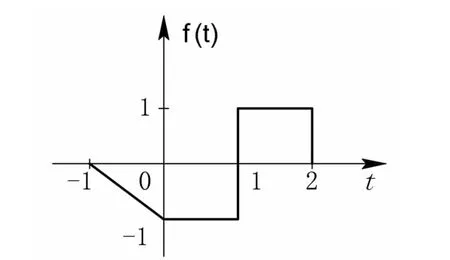
图2.1 信号f（t）的波形

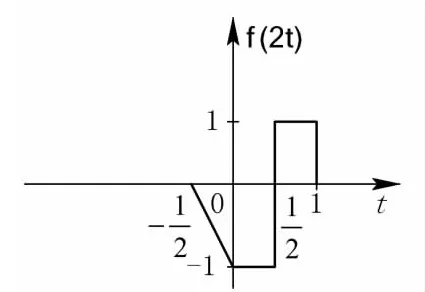
图2.2信号f（2t）的波形

图2.3信号f（2t+1）的波形

其次，对f（2t）的波形进行移位运算。这里需要特别注意的问题是，平移方向是往左还是往右?平移单位又是多少?这是本篇文章研究的一个重点问题。

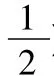
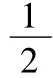
最后，对f（2t+1）的波形进行翻转运算。即可得到f（1－2t）的波形如图2.4所示。

图2.4信号f（1－2t）的波形

图2.5信号f（t+1）的波形

为了进一步说明信号的运算只针对自变量t来 进行，我们按照先移位，再反褶，最后进行尺度变换的顺序，来得到f（1－2t）的波形。

首先，对f（t）波形进行移位运算。根据前面所讲述的两点要点可知，在已知f（t）波形的前提下，将f（t）波形向左平移1个单位，得到f（t+1）的波形，如图2.5所示。注意在移位时，不必考虑自变量t前 面的负号，如果考虑负号，则是对信号f（－t）进行平移。

其次，对f（t+1）波形进行反褶运算。以坐标原点为圆心，绕y周旋转180°，则得到f（－t+1）的波形。如图2.6所示。

图2.6信号f（－t+1）的波形

图2.7信号f（1－2t）的波形

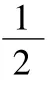
同理，我们也可以根据先反褶，再尺度变换，最后移位的顺序得到f（1－2t）的波形，结果同前两种方法一样。运算的重点在于移位，而移位的重点在于平移方向和平移单位，如前强调，所有的运算都是针对自变量t来进行，只有遵循这个规律，在运算过程中才不容易出错。

三、总 结

信号在传输过程中，往往出现移位、反褶和尺度倍乘等运算，通常接收到的信号总是伴随着两种或两种以上的运算。在信号运算过程中，如果将移位，反褶和尺度倍乘混淆，则会造成不必要的运算错误，尤其是信号的移位问题，平移方向和平移单位是重点。本文在移位、反褶以及尺度倍乘等基本运算的基础上，以信号的移位运算为主要研究对象，就信号移位这个关键且容易出错的问题进行了细致的讲述，旨在使读者们更能明白其重要性。