一种基于代谢网络分析最小化基因组的方法及其在大肠杆菌中的应用
2013-09-04汤彬彩郝彤袁倩倩陈涛马红武
汤彬彩,郝彤,4,袁倩倩,3,陈涛,马红武,3
1天津大学化工学院生物工程系,天津 300072
2天津大学 教育部系统生物工程重点实验室,天津 300072
3中国科学院天津工业生物技术研究所 中国科学院系统微生物技术重点实验室,天津 300308
4天津师范大学生命科学学院,天津 300387
随着2010年5月美国生物学家文特尔等在Science杂志发表了关于由化学合成的基因组控制的细胞的文章[1],人工合成生命的研究引起了广泛的关注。构建最小生命体一直是人工合成生命的重要内容之一,文特尔的工作再次引发了研究者们对最小基因组的研究兴趣。
最小基因组是指在最适宜的条件下,维持细胞生长繁殖所必需的最小数目的基因,在最小基因组中,敲除任何基因后细胞都会死亡。在不同培养条件下,得到的最小基因组可能是不一样的,这与生物本身的合成能力有关,所以最小基因组是相对而言的。在代谢工程研究领域中,人们关心更多的是如何得到一个最小化的基因组而同时保持细胞的生长不受影响。
目前对最小基因组的研究在湿实验方面已经取得了一些进展,1995年起研究者开始对生殖支原体进行研究[2],因为生殖支原体是能够自主复制并生存的最小细胞生物,其基因组只有580 kb,2007年Lartigue等将生殖支原体整个基因组转移到掏空的山羊支原体里[3]并使之成活,2008年Gibson等人工合成整个生殖支原体[4],这些工作体现着研究者们对获得人工合成最小生命的不断探索。除了“自下而上”地从头合成基因组外,另一个研究思路是从已有物种出发,通过“自上而下”地逐步敲除基因,去除细胞中的冗余基因,得到最小基因组。例如,Posfai等通过大片段基因敲除成功将Escherichia coliK-12基因组减少了15%[5]。同时这一小基因组大肠杆菌还具有一些意想不到的特性:比如高效的电转化率,准确的复制重组基因和稳定的质粒复制等。这揭示了在大肠杆菌中并非所有的基因都是必需的,通过大量删除基因,可以获得具有新性能的微生物。根据这一思路,必需基因[6-7]的确定是获得最小基因组的重要依据。但最小基因组中除了这些必需基因外还需要包括其他的基因,这些基因虽然单独敲除不会对细胞产生影响,但两个或多个同时敲除时则可能导致细胞死亡。如何找出这些非必需但又需要包含在最小基因组中的基因是目前研究中面临的一项重要挑战。而基因组规模代谢网络则有可能为解决这一问题提供可能性。
基因组尺度的代谢网络模型指的是以注释信息及基因序列为基础,利用基因-蛋白质-反应的关系为主线,成功模拟代谢物在生物机体内的过程的一种包含大量信息的模型,到2012年6月为止已经构建完成135个基因组尺度代谢网络模型,涉及64种原核生物、19种真核生物和4种古生菌 (GSMNDB:http://synbio.tju.edu.cn/GSMNDB/gsmndb.htm)。国内外已经有数篇关于基因组尺度代谢网络模型重构以及模拟方法的综述[8-12],模型在模拟基因敲除、靶点药物发现、扰动实验预测以及物种进化研究方面都有着重要作用[13]。
虽然最小基因组的研究在湿实验方面已经有了一些进展,但是到目前为止还没有一个完整的关于最小基因组的代谢网络模型和计算方法,Yizhak等[14]注重研究基因敲除与合成生物量之间的关系,Pa等[15]构建的模型只是对于模型的简化,并没有得到一个不能删除任何基因的最小基因组模型。在本文中我们按照“自上而下”的研究思路,通过对基因组尺度代谢网络模型的逐步精简第一次获得最小基因组代谢网络模型。
1 方法
1.1 通量平衡分析方法
在基因组规模代谢网络模型分析中较为广泛应用的是基于约束的最优化方法,这一方法主要由决策变量、约束条件和目标函数三部分组成,本文采用其中的通量平衡分析 (Flux balance analysis,FBA)[16-17]方法进行模拟计算,在FBA中,决策变量就是模型中所有反应的通量值,不同的通量分配方案决定着不同的代谢状态,限制条件是实现最优化模拟必须满足的基本条件,包括等式限制和不等式限制,等式限制条件基于拟稳态条件下所有中间代谢物满足物质守恒的假设,即代谢物的生成与消耗相等,而不等式限制基于模型中每个反应速度的极限值。约束条件表示为数学形式如下:
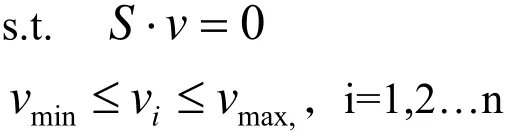
其中,vmin和vmax分别表示反应速度的最小和最大值,在本文中,在没有特殊限制条件下,对于可逆反应,其最小值和最大值分别为−1 000和1 000 mmol g/(DW·h),而对于不可逆反应,其最小值和最大值则分别为0和1 000 mmol g/(DW·h)。目标函数在数学上可以表示为决策变量的解析函数 (即一系列决策变量的线性或非线性组合),根据不同的模拟目的,目标函数既可以只有一个,也可以同时有多个,本文的目标是在保持细胞生长不受影响的情况下将基因组最小化,因此以生物量的最大速率为目标函数。在本文中当一个基因被敲除后,生物合成量的模拟值小于最初模型的生物合成量,这样的基因被定义为必需基因。我们利用的计算工具是Matlab平台下运行的COBRA[18]工具包。
1.2 通量可变性分析
通量可变性分析 (Flux variability analysis,FVA)[19]是在FBA基础上发展的通量分析方法。FBA计算出来的最优解不是唯一的,有多种通量分布可以使目标反应达到最优值。FVA就是在保证目标反应在最优值的情况下得到每个反应的通量的可能最大值和最小值,从而得到每个反应的通量变化范围。我们定义那些通量变化范围总是大于0或总是小于0的反应为达到最优解的必需反应,因为这些反应对每个最优解都是必须要存在的。这里要说明的是必需反应对应的基因并非都是必需基因,因为一个反应可能有多个同工酶基因对应。除了必需反应外的其他反应定义为非必需反应,这些非必需反应可以单个敲除但并不能同时敲除。
1.3 组合删除法
在代谢网络中从代谢物A到B可能有多个不同的代谢途径,如图1所示,从A到B可以通过A-X-B、A-Y-Z-B和A-M-N-O-B三条路线实现,显然A-X-B途径最短。因而需要考虑的问题是如何保证在精简的代谢网络中从代谢物A到B需要通过的途径是基因X而不是Y-Z或者M-N-O。我们采用的方法是将参与从A到B所有途径的基因{X,Y,Z,M,N,O}进行分步组合模拟删除,首先进行单基因敲除实验,发现可被敲除的基因数目即非必需基因数目为6个,第一步从这6个基因里取出6个基因组合模拟删除,看能否得到代谢物B,只有一种取法C(6,6)=1,很明显不能,那我们就从6个基因里选出5个基因进行组合,共有C(5,6)=6种选法,每种选法都进行一次模拟删除,看能否得到代谢物B,在本例中当选取的组合为{Y,Z,M,N,O}的时候,代谢物A能够生成B,最后保留的基因数目就为6(所有非必需基因数目)−5(选取组合包含基因的数目)=1(非必需基因保留的数目),我们将这种思想运用到整个模型上,以葡萄糖为底物,生物量合成为目标函数,利用程序对非必需基因进行逐步递减组合模拟删除,在保证生物量不变的情况下,保留删除基因最多的反应途径在模型中,最后得到基因组最小化的代谢网络模型。

图1 从代谢物A到B的代谢途径示例Fig.1 Metabolic pathways from metabolite A to B.
1.4 基因组简化的步骤
整个基因组简化步骤如图2所示,主要包括以下步骤:
1)对初始代谢网络模型进行FVA分析,其中有很多反应的最大通量和最小通量都为0,即这些反应与细胞最优生长无关,因而首先将这些反应从网络中删除。

图2 基因组最小化的步骤 (图中数字为各步处理后的基因数)Fig.2 Procedure of genome minimization.The numbers of genes after every step are shown in the diagram.
2)处理同功酶基因。在模型中有很多同功酶基因催化同一反应的情况,这些基因只需存在一个 (组),反应就能够进行,因而多余的基因可以去除。需要注意的是在这些同功能基因中,有些同时催化多个反应,其中有些反应是菌体生长所必需的,因而简单地去除每个同功能基因可能导致菌体的死亡,因而我们仅将只催化单个 (一类)反应的同功能基因去除,而同时催化多个反应的同功能基因则保留下来进行进一步计算。
3)经过上述两步我们得到了部分缩减的代谢网络模型,通过FVA分析模型中的反应分为必需反应和非必需反应两部分,在此基础上我们将该模型中的基因分为两个子集:保留基因集和候选基因集。所有必需反应中的基因构成保留基因集,要提出的是有的必需反应是有几个同功能基因催化的,只要保证该必需反应能够进行,多余的基因是可以被删除的,所以保留基因集并不等于所有基因都保留,除了保留基因以外的基因则为候选基因集。
4)保留基因集的基因组最小化,利用单基因敲除函数找出必需反应部分可以敲除的基因,通过组合删除方法进行筛选,找到必需反应部分对应的最小基因组。
5)候选基因集的基因组最小化,在4的基础上,同样利用单基因敲除函数找出可以被敲除的基因,因为非必需基因数目较多,但由于4步骤中对应必需反应的非必需基因已经在前一步进行了单独处理,大部分必需基因得到保留,因而在做组合删除的时候运算量大大减少。最后得到的新模型就是该物种模型的基因组最小化代谢网络模型。
2 结果与分析
2.1 由代谢网络分析进行大肠杆菌基因组最小化
大肠杆菌是目前了解得最清楚、分析得最透彻的微生物之一,是遗传学研究、生化研究和代谢模拟研究的重要平台,大肠杆菌作为遗传重组领域广泛应用的宿主之一,在医药和发酵工业中可用于生产重组蛋白、氨基酸和其他化学品。因为大肠杆菌在动物肠道和环境中进化其部分基因组对某些用途是不需要的,甚至可能是有害的,因此,通过删除尽可能多的基因片段,构建遗传稳定的菌株,可使大肠杆菌具有健壮的代谢行为,同时也可以添加具有实际用途的基因。
目前大肠杆菌的基因组尺度代谢网络模型共有 4 个,包括iJE660[20]、iJR904[21]、iAF1260[22]和iJO1366[23],iAF1260在必需基因预测及与实验结果的拟合度上准确率较好,所以本文采用iAF1260模型作为出发模型,培养条件设定为最小培养基。葡萄糖为唯一碳源,其通量设定为−8 mmol g/(DW·h)。最优生物合成速率为0.7367 mmol g/(DW·h)。
通过前文方法部分介绍的步骤,我们对基因组尺度代谢网络模型分步骤进行简化,各步骤结果 (图2)如下:
1)我们首先删除模型中的经过FVA分析后的0通量反应,在2 382个反应中共有1 535个反应在FVA结果中的代谢通量为0,最后将0通量反应删除后,得到847个反应,对应731个基因。我们将由这些反应构成的新模型称为model1,将其转化为新的SBML文件 (数据未显示),以便于进行下一步的计算。
2)优化网络,去除仅催化一个或一类反应的同功酶基因,这样的基因共有100个,因而得到的模型 (model2)包含847个反应,对应631个基因,将其重新转化为新的SBML文件 (数据未显示),以便于进行下一步计算。
3)通过对FVA结果的分析,model2模型中必需反应部分包含366个反应,对应有305个基因,利用单基因敲除函数,找出非必需基因40个 (具体数据作为附件,可在网络版中下载。下文简称“附件”),对这40个基因进行逐步递减组合模拟删除,最后确定其中26个基因 (附件)敲除后对菌体生长没有影响,这部分基因敲除后整个模型包含841个反应,605个基因。此时必需反应部分中无任何基因可以被敲除,规模达到最小。我们将由这些反应构成的新模型称为(model3),将其转化为新的SBML文件 (数据未显示),以便于进行下一步的计算。
4)将model3的非必需反应部分进行基因组最小化,同样利用单基因敲除函数找出非必需基因,其数目为304个 (附件),对这些非必需基因,我们采用组合法进行删除,在保证合成生物量不变的情况下,依次从里面取出304个基因、303个基因、302个基因……,以此类推,进行模拟删除,当取出293个基因 (附件)删除的时候得到一种组合方式,满足条件,所以非必需基因保留的最小值就是304−293=11(个),最终得到含有403个反应,对应312个基因的模型model4,将该模型转化为SBML文件 (数据未显示)。
5)将新模型model4再次进行单基因敲除实验,发现可以敲除的基因数目为0,这验证了利用这一方法得到的确实是最小基因组。利用该基因组最小化的代谢网络模型,在葡萄糖输入设定为−8 mmol g/(DW·h)时求得最优生物质合成速率为0.7367 mmol g/(DW·h),与原始模型相同,表明基因组精简后,菌体生长不受影响。整个模型简化过程中各个步骤的结果如表1、图2、图3及附件所示。
从表1、图3可以看出在简化基因组的过程中,FVA分析和非必需反应部分删除的基因和反应占所有删除的基因和反应数目的大部分,这符合生物学的特征,最后整个基因组缩小为原来的24.7%,这也为湿实验寻求敲除目标基因部分提供参考。
2.2 最小基因组代谢网络模型途径分析
为了进一步了解得到的基因组最小化代谢网络模型的特征,我们对模型中反应的代谢途径分布进行了分析。模型中的403个反应分布在32个代谢途径中,具体分布情况如表2所示。

表1 基于代谢网络模型的大肠杆菌基因组最小化结果Table 1 Minimization of E.coli genome based on metabolic network analysis
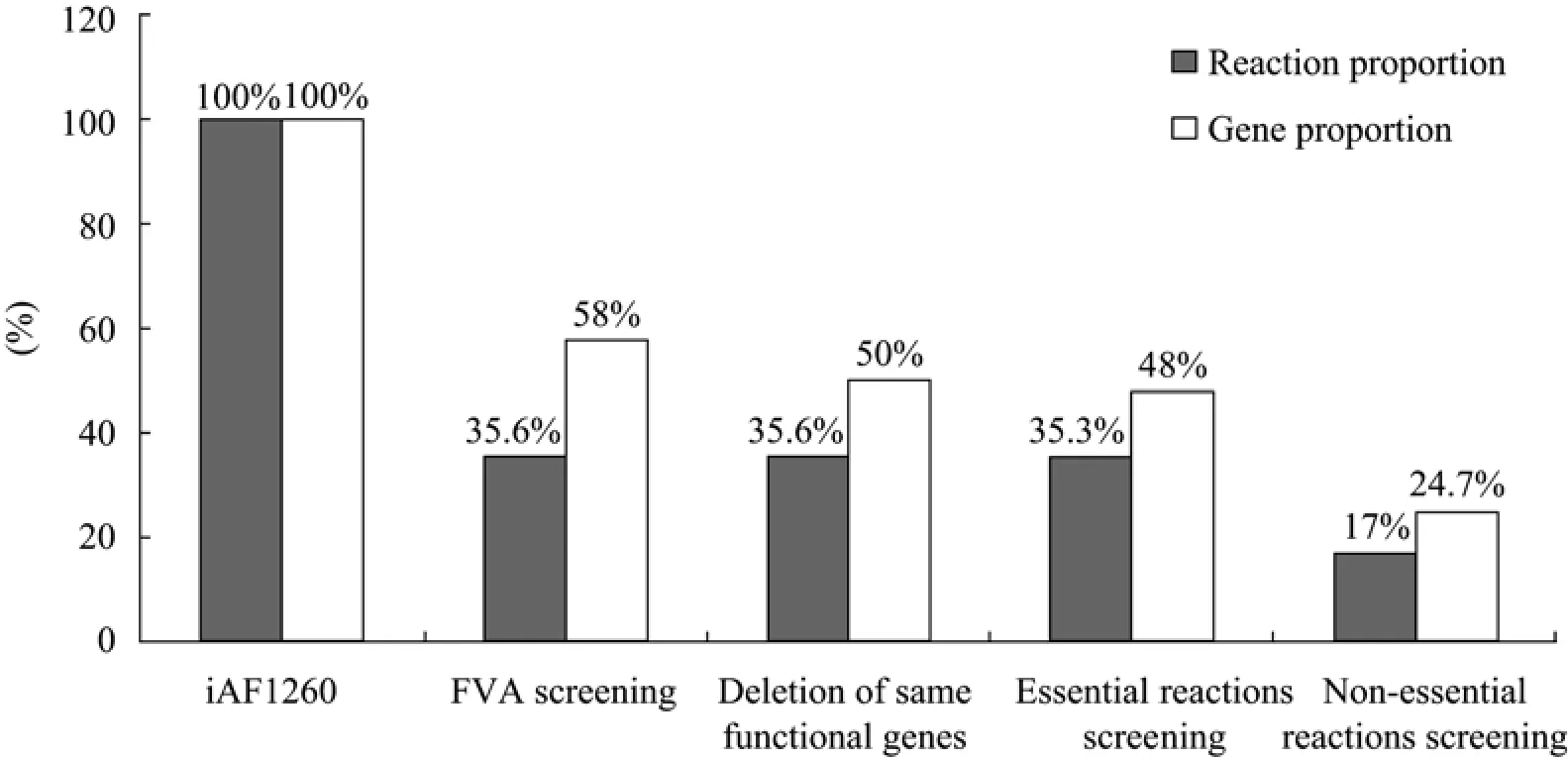
图3 每个步骤后的基因数目和反应数与初始模型的比较结果Fig.3 Comparison of the gene number and the reactions number with the initial model after every step.
从表2可以看出在基因组最小模型中,氨基酸代谢和脂类代谢包含的反应数最多,分别为112个和80个,这表明大肠杆菌的生长过程中,氨基酸、脂类代谢具有最为重要的作用,这与氨基酸和脂类物质在大肠杆菌细胞组成中占有较高比例相符。另外,辅因子代谢包含77个反应,在整个网络中也具有很大的比重,这表明辅因子是合成生物量不可缺少的重要成分。另外要注意的一点是交换反应在模型同样具有重要的作用,任何基因组最小化的模型都是相对的,当培养基条件发生改变时,模型包含的交换也会发生改变,交换反应越多时,表明外界提供的营养物质越多,则菌体自身合成的物质越少,从而模型所包含的反应数和基因数都会相应的减少。
另外,从碳源的利用上来看,在基因组最小化模型模拟中乳酸的合成途径完全被删除,其他副产物乙酸、琥珀酸合成途径通量也为零,表明底物充分用于生物量的合成,去除了分流到其他副产物而产生的碳源消耗,该结果显示了基因组最小化代谢网络模型对生物代谢途径的优化。
2.3 与湿实验结果的比较
湿实验方面,Posfai等[5]通过大片段基因敲除成功将E.coliK-12 MG1655基因组减少了15%,构建了 MDS40、41、42和 43菌株,Kolisnychenko等将大肠杆菌[24]基因组减少了 8.1%,构建了MDS12菌株,Hashimoto等[25]将大肠杆菌基因组减少了29.7%构建了△16菌株,但其类核组织表现异常,生长速率较低,在M9培养基上无法生长。同时Mizoguchi等[26]通过无痕敲除方法删除了103个候选区域,共删除1 080个基因,有84个删除突变株的生长行为与野生株类似,将这些删除累积起来构建了一个基因组减小菌株——MGF-01。Hirokawa等[27]在MGF-01的基础上继续删减得到结构稳定,没有任何营养缺陷性的,可以更高效生长的菌株——DGF-327和DGF-298。我们综合考虑选用MDS43和DGF-298菌株与模型相比较,因为这两种菌株的生产速率与野生型类似,且稳定性强,电转化效率高。

表2 大肠杆菌基因组最小化代谢网络模型的代谢途径分布Table 2 Metabolism pathways of the minimized metabolic network in E.coli
Posfai等[5]通过构建的基因组缩减菌株MDS43共敲除了743个基因,iAF1260模型中包含其中的82个基因,这82个基因在基因组最小化模型并没有被全部去除 (附件),其中5个基因仍然保留在模型中,这5个基因是b0339(cynt)、b2976(glcb)、b2979(glcd)、b4467(glcf) 和 b4468(glce)。b0339、b2976两个基因在原有模型当中都具有同功酶,即处于“or”的关系,由于组合删除的随机性,导致删除了与其同功能的基因,而保留了这两个基因,这一点对于菌体生长并没有影响。而剩下的3个基因 (b2979、b4467和b4468)构成一酶复合物催化反应GLYCTO2(Glycolate+Q8=Glyoxylate+Q8H2)。该反应可以将代谢网络中某些反应过程生成的乙醇酸转化为乙醛酸,进而通过乙醛酸循环转化为生物质合成需要的前体。我们注意到大肠杆菌代谢网络模型中还有另外两个基因 (b1033、b3553)催化乙醇酸和乙醛酸间的转化但所用辅酶为NADH或NADPH(R_GLYCLTD:Glycolate+NAD(P)<==>Glyoxylate+NAD(P)H2),但该反应被定义为不可逆且反应方向为从乙醛酸到乙醇酸。当我们将该反应改为可逆后进行基因组最小化计算得到的最小基因组中就不包括b2979、b4467和b4468而是只包括b1033或b3553,基因个数也从312个减少到了310个。这表明大肠杆菌中很可能反应R_GLYCLTD也是可逆的,因此敲除b2979、b4467和b4468这3个基因对生长没有影响。
我们还将得到的最小基因组与Hirokawa等[27]构建的 DGM-298菌株进行了比较,DGF-298一共删除了1 429个基因,其中iAF1260模型中包含被实验证明可被删除的基因数为298个 (附件),同样这298个基因在基因组最小化模型中并没有被全部去除,其中有12个基因仍保留在最后的模型当中,分别是b0149(mrcb)、b0339(cynt)、b0381(ddla)、b0521(ybcf)、b1415(alda)、b2097(fbab)、b2708(gutq)、b2797(sdab)、b2979(glcd)、b3744(asna)、b4094(phnn)、b4467(glcf) 和 b4468(glce)(附件)。其中 b0149、b0339、b0381、b4383、b0521、b2097、b2708 和 b2797七个基因是因为同功能基因,即“or”关系的选择而被保留在模型中。b2979、b4467和b4468三个基因在上一部分已经说明是因为模型中一些反应的可逆性设置的问题。b1415和b3744两个基因所催化的反应分别是gcald+h2o+nad<==>glyclt+nadh和asp-L+atp+nh4<==>amp+asn-L+ppi,这两个反应在模型中以葡萄糖为唯一碳源时为必需反应。而Hirokawa等采用的是富培养基,可以从培养基中直接得到天门冬酰胺等而不需要从葡萄糖生成,因此在其湿实验中可以敲除而在我们的模拟计算中保留在最小基因组中。
从上面的结果可以看出,当需要敲除某些基因的时候,可以利用得到的最小基因组模型反馈于湿实验,确定哪些基因可以尝试敲除,哪些途径可以得到保留,模拟的结果为湿实验的设计提供了有价值的参考。
3 结论与展望
现代生物技术的高速发展,特别是组学技术的兴起,高通量数据的迅速积累,促进了生物代谢网络模型的快速发展,使网络构建的理论逐渐完善,质量大幅度提升,应用范围同样也显著扩大,在此基础上,本文第一次提出了基于基因组尺度代谢网络模型,通过模型简化构建基因组最小化代谢网络模型的方法,该方法通过零通量反应删除和对非必需基因的组合删除模拟计算,确定能够计算的基因组最小化代谢网络模型。该方法依托于超级计算机的计算能力,运用Matlab中的COBRA工具包,以大肠杆菌的iAF1260模型为例,将模型从最初的1 260个基因缩减到312个基因,模型简化后生物量合成速率保持不变。通过该方法得到的基因组最小化代谢网络模型中氨基酸代谢及脂类代谢仍为生物体生长的主要需求,符合生物代谢规律,证明了基于非必需基因组合的删除方法的合理性。
通过对基因组尺度代谢网络模型的精简,我们可以确定对于生物生长最为重要的反应和基因,并且得到相应代谢途径、代谢系统的生物信息,通过计算机模拟得到的结果可以为湿实验的方案设计提供重要的参考。由于该方法是在基因组尺度代谢网络模型的基础上实施的,因而高质量的模型对于最终得到的基因组最小化代谢网络模型非常重要,基因组最小化代谢网络模型对于今后专一生产某种代谢物的途径设计也将提供更好思路。另外,随着网络模型的发展,基因组最小化代谢网络模型中也可能会结合调控、信号转导等信息,使基因组最小化的生物网络向更加趋近于最小生命体的方向发展。
[1]Gibson DG,Glass JI,Lartigue C,et al.Creation of a bacterialcell controlled by a chemically synthesized genome.Science,2010,329(5987):52−56.
[2]Fraser CM,Gocayne JD,White O,et al.The minimal gene complement ofMycoplasma genitalium.Science,1995,270(5235):397−403.
[3]Lartigue C,Glass JI,Alperovich N,et al.Genome transplantation in bacteria:changing one species to another.Science,2007,317(5838):632−638.
[4]Gibson DG,Benders GA,Andrews-Pfannkoch C,et al.Complete chemical synthesis,assembly,and cloning ofaMycoplasmagenitaliumgenome.Science,2008,319(5867):1215−1220.
[5]Posfai G,Plunkett G,3rd,Feher T,et al.Emergent properties of reduced-genomeEscherichia coli.Science,2006,312(5776):1044−1046.
[6]Juhas M,Eberl L,Glass JI.Essence of life:essential genes of minimal genomes.Trends Cell Biol,2011,21(10):562−568.
[7]Qiu DR.Essential genes,minimal genome and synthetic cell of bacteria:a review.Chin J Biotech,2012,28(5):540−549(in Chinese).
邱东茹.细菌必需基因、最小基因组和合成细胞.生物工程学报,2012,28(5):540−549.
[8]Durot M, Bourguignon PY, Schachter V.Genome-scale modelsofbacterialmetabolism:reconstruction and applications.FEMS Microbiol Rev,2009,33(1):164−190.
[9]Thiele I,Palsson BO.A protocol for generating a high-quality genome-scale metabolic reconstruction.Nat Protoc,2010,5(1):93−121.
[10]Feist AM, Herrgard MJ, Thiele I, et al.Reconstruction of biochemical networks in microorganisms.Nat Rev Microbiol,2009,7(2):129−143.
[11]Park JM,Kim TY,Lee SY.Constraints-based genome-scale metabolic simulation for systems metabolic engineering.BiotechnolAdv,2009,27(6):979−988.
[12]Hao T,Ma HW,Zhao XM.Progress in the automatic reconstruction of genome-scale metabolic network.Chin J Biotech,2012,28(6):661−670(in Chinese).
郝彤,马红武,赵学明.基因组尺度代谢网络自动重构及分析工具研究进展.生物工程学报,2012,28(6):661−670.
[13]Wang H,Ma HW,Zhao XM.Progressin genome-scale metabolic network:a review.Chin J Biotech,2010,26(10):1340−1348(in Chinese).
王晖,马红武,赵学明.基因组尺度代谢网络研究进展.生物工程学报,2010,26(10):1340−1348.
[14]Yizhak K,Tuller T,Papp B,et al.Metabolic modeling of endosymbiont genome reduction on a temporal scale.Mol Syst Biol,2011,7:479.
[15]Pal C,Papp B,Lercher MJ,et al.Chance and necessity in the evolution of minimal metabolic networks.Nature,2006,440(7084):667−670.
[16]Orth JD,Thiele I,Palsson BO.What is flux balance analysis?Nat Biotechnol,2010,28(3):245−248.
[17]Edwards JS,Palsson BO.Metabolic flux balance analysis and the in silico analysis of Escherichia coli K-12 gene deletions.BMC Bioinformatics,2000,1:1.
[18]Schellenberger J,Que R,Fleming RM,et al.Quantitative prediction of cellular metabolism with constraint-based models:the COBRA Toolbox v2.0.Nat Protoc,2011,6(9):1290−1307.
[19]Muller AC,Bockmayr A.Fast thermodynamically constrained flux variability analysis.Bioinformatics,2013,29(7):903−909.
[20]Edwards JS,Palsson BO.TheEscherichia coliMG1655 in silico metabolic genotype: its definition,characteristics,and capabilities.Proc Natl Acad Sci USA,2000,97(10):5528−5533.
[21]Reed JL,Vo TD,Schilling CH,et al.An expanded genome-scale model ofEscherichia coliK-12(iJR904 GSM/GPR).Genome Biol,2003,4(9):R54.
[22]FeistAM,Henry CS,Reed JL,etal.A genome-scale metabolic reconstruction forEscherichia coliK-12 MG1655 that accounts for 1260 ORFs and thermodynamic information.Mol Systems Biol,2007,3(121):1−18.
[23]Orth JD,Conrad TM,Na J,et al.A comprehensive genome-scale reconstruction ofEscherichia colimetabolism—2011. Mol Systems Biol, 2011,7(535):1−9.
[24]Kolisnychenko V,Plunkett G 3rd,Herring CD,et al. Engineering a reducedEscherichiacoligenome.Genome Res,2002,12(4):640-647.
[25]Hashimoto M,Ichimura T,Mizoguchi H,et al.Cell size and nucleoid organization ofengineeredEscherichia colicells with a reduced genome.Mol Microbiol,2005,55(1):137−149.
[26]Mizoguchi H,Mori H,Fujio T.Escherichia coliminimum genome factory. Biotechnol Appl Biochem,2007,46(Pt 3):157−167.
[27]Hirokawa Y,Kawano H,Tanaka-Masuda K,et al.Genetic manipulations restored the growth fitness ofreduced-genomeEscherichiacoli.JBiosci Bioeng,2013,1(10):1−7.
