车门抗凹陷性能分析研究
2013-09-04谯万成羊定侯贺方平
谯万成 羊定侯 贺方平
(一汽海马汽车有限公司)
1 前言
车门系统是外覆盖件中的一个子系统,是客户直观评价外覆盖件抗凹陷性能的主要系统。车门抗凹陷性能是车门外板在载荷作用下抵抗凹陷变形的能力。抵抗变形能力的大小取决于车门结构的几何形状和零件的材料属性。根据抗凹陷试验方法,本文采用一汽海马公司传统的抗凹陷仿真分析方式与改进后的仿真分析方式分别进行CAE仿真,并与试验结果进行对比,考察两种仿真分析结果与试验结果的差异性,为抗凹陷仿真分析提供更好的方法。
2 车门抗凹陷试验
在凹陷性台架试验机上,对某车型前车门进行试验,在前车门外板上选取按单位间距排列的点进行逐个测试,以验证整个车门的抗凹陷性能。取值时,对车门所有测试点在每个额定载荷作用下读取一个相对应的位移值。本文随机选择其中一个测试点进行对比分析,台架试验如图1所示。
根据凹陷性试验方法,在搭建CAE仿真分析模型时,可简化为被测区域在外力作用下发生凹陷,其试验作用过程如图2所示。
抗凹陷性能主要由被测点的最大变形量、残余变形量、易拉罐效应3个性能指标进行评判。通过多个试验结果数据的整理与分析,可知这3个评价指标之间并不存在任何相对应的数值关系。
3 有限元模型搭建
模拟台架加载方式搭建相应的有限元仿真模型,基于HyperMesh前处理搭建车门子系统基础网格模型。
传统抗凹陷性仿真分析方式与改进后的抗凹陷性仿真分析方式载荷大小与载荷方向相同,最主要差别在于载荷的施加方式不同。传统仿真分析方式是在HyperMesh的ABAQUS模块中对被测区域表面施加额定压强;改进后的仿真分析方式是在ABAQUS_CAE模块中处理,建立刚性球,对钢性球施加额定集中载荷,使用钢性球挤压被测区域[1]。
两种仿真方式均采用ABAQUS隐式求解器求解。
3.1 抗凹陷性能隐式求解理论
隐式算法基本上采用纽曼法进行时间域的积分,由连续介质力学理论得到系统的运动方程为:
式中,M为质量矩阵;C为阻尼矩阵;K为刚度矩阵;a为加速度;v为速度;u为位移;F为作用力。
Newmark—beta隐式积分一般形式为:
式中,n为迭代次数;Δt为时间增量;β、γ为常数。
采用4节点单元进行有限元离散化时,γ=1/2,β=1/4,可得:
式中,内力 R=乙βTσdv。
为消除线性化带来的误差,采用牛顿—拉弗森法进行平衡迭代,迭代求解平衡方程为:
式中,kt(u)为增量步开始时的切线刚度矩阵。
第一次求解得到Δu=Δu1,下一次迭代有:
解得 Δu=Δu2,反复迭代得到:
迭代收敛条件为位移收敛条件,即:
式中,i为迭代次数号;FRCTOL为定义的收敛容差。
在求解过程中,若迭代既没有收敛也没有发散,则按式(9)进行位移修正:
继续进行平衡迭代,一直到得到收敛的解[2],求出抗凹陷性能的位移值。
3.2 被测点网格细化
为了更好的模拟试验台架,需要对试验台架触头与车门外板接触部分做直径为12 mm范围面积的网格细化。
外表面被测区域中心的网格最细,网格大小可以控制在0.5 mm×0.5 mm内;只允许出现极少数的三角形网格;网格围绕中心区域向四周扩散,网格大小逐渐变大。网格细化后得到的典型网格分布如图3所示。为提高仿真精度,细化的网格与周围网格连接时,应避免不合格网格的出现。
3.3 材料与属性
传统高强度钢板屈服应力大、强度高,但其冲压成形性较差,特别是起皱、回弹等缺陷比较明显。车辆外覆盖件材料选择则需要考虑外覆盖件的抗凹陷性能。该车门外板采用的材料为经过烘烤硬化的高强度钢板(BH钢),其不仅具有良好的刚度、强度,还具有优良的抗凹陷性能[3]。该种材料与传统钢材的抗凹陷性能对比如图4所示。
在建立抗凹陷仿真分析有限元模型时,根据材料试验得到该材料的弹性模量、密度、泊松比以及材料的应力应变曲线。经过处理后的材料应力应变曲线如图5所示。
3.4 边界条件
两种载荷施加方法的仿真约束方式相同,均采用和台架试验一致的约束方式,载荷施加方向与被测点表面的法向相同。车门门锁处以及车门上下铰链约束整车坐标系下X、Y、Z轴向平动自由度,车门限位点约束2自由度,约束方式如图6所示。
第一种载荷施加方式为压强,在前车门外表面被测区域内施加压强。根据台架试验的载荷值以及触头与车门接触的面积,算出施加到被测点每一个网格单元上的平均压强值为0.442MPa,压强与接触面积的乘积为200N。搭建完成后的模型如图7所示。
搭建第二种载荷施加模型时,需要在ABAQUS的前处理界面创建属性为解析刚体的直径为80 mm的刚性球,将集中载荷200 N加载于刚性球上,再让刚性球作用于车门被测点。通过建立刚性球外表面与被测表面之间的接触属性以及摩擦关系,保证刚性球挤压被测表面过程中更接近抗凹陷台架试验的整个测试状态。搭建模型时,建立以车门外表面被测点为坐标原点、其中一个方向坐标轴垂直于被测表面的局部坐标系。集中载荷作用在刚性球上的方向为局部坐标系下垂直于被测表面的坐标轴。对刚性球进行约束时,在局部坐标系下放开沿被测点表面法向一致的平动自由度,其余方向全约束[4]。搭建完成的模型如图8所示。
考虑到抗凹陷台架试验中加载是一个缓慢的过程,仿真分析的载荷可近似为线性的加载与卸载,载荷曲线如图9所示。
4 仿真计算结果分析
4.1 第二种载荷施加方式作用过程
刚性球与被测点之间的相互作用是一个连续的过程,作用力与位移云图如图10所示。
4.2 两种载荷施加方式作用结果
两种不同的载荷施加方式导致的最大变形与残余变形结果如图11、图12所示。
4.3 仿真结果与试验对比
根据试验所得的数据,制作载荷位移曲线,将两种不同载荷施加方式的仿真结果与试验曲线进行对比如图13所示。
前车门抗凹陷性能台架试验结果最大变形量为10.21 mm,残余变形量为0.192 mm;第一种载荷施加方式计算所得的最大变形量为11.16 mm,残余变形量为0.12 mm;与试验结果相比最大变形量的相对误差为13.6%,残余变形量的相对误差为36.5%。第二种载荷施加方式计算所得的仿真结果最大变形量为10.62 mm,残余变形量为0.16 mm;与试验结果相比最大变形量的相对误差为4.0%,残余变形量的相对误差为17.7%。
在整个车门外表面台架试验中随机选择6个测试点,除去文中所述的测试点,其余5个测试点测得的结果与计算机仿真分析所得的结果如表1所列。通过仿真与试验结果对比可知,某些测试点最大变形量不满足要求,但是残余变形量满足要求;某些测试点则是最大变形量满足要求,但是残余变形量不满足要求。对于固定载荷、固定钢性球直径测试方式,可以按照试验要求的目标作为评价标准。
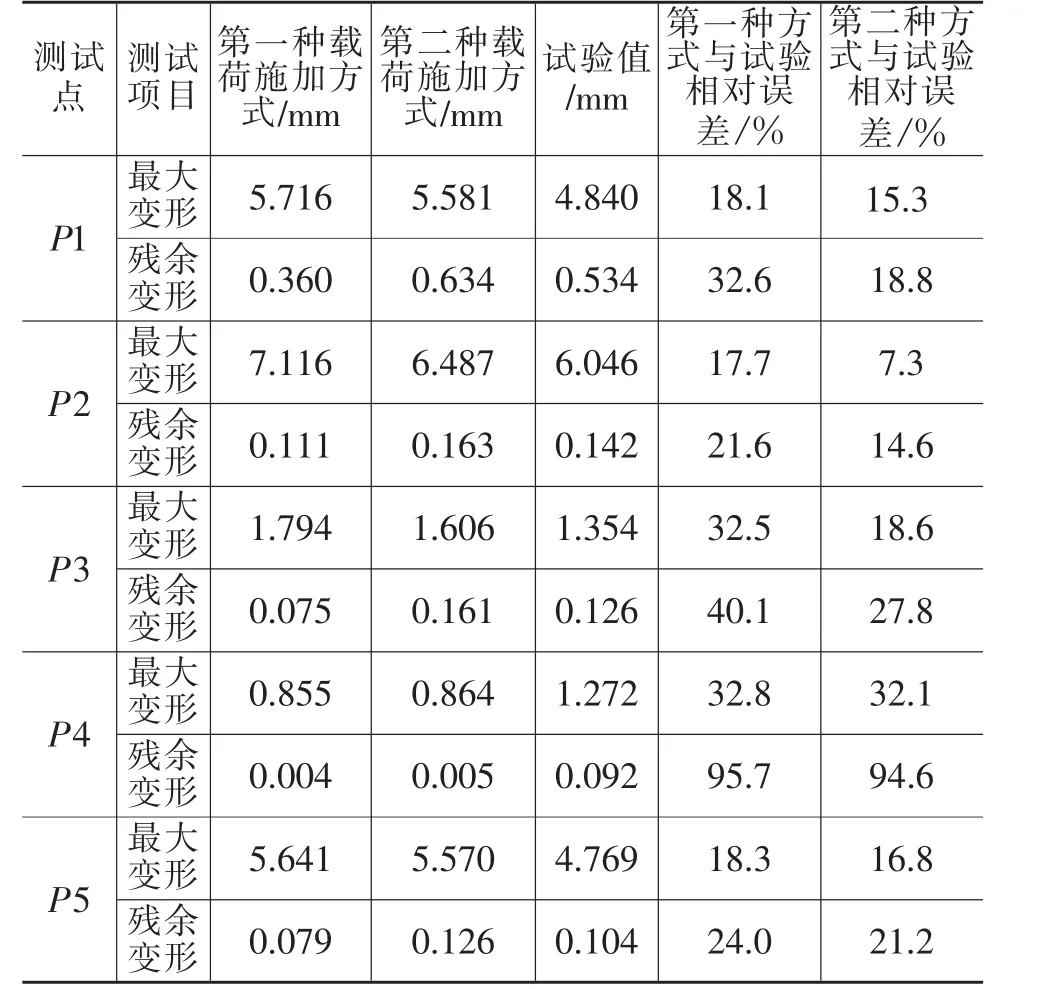
表1 仿真与试验结果
从表1中误差分析情况可以看出,第二种载荷施加方式与试验更加接近。
5 结束语
建立刚性球,创建外表面接触以及摩擦参数,是一种更加接近试验的模拟仿真手段,其不仅局限在车门上,还适用于车身外覆盖件的各个子系统上,包括挡泥板、翼子板、发动机盖板、后背门盖板抗凹陷性能仿真分析中。
经过一系列的试验对比研究,第二种载荷施加方式更能反映外覆盖件承受凹陷变形的能力,为汽车外覆盖件设计提供可靠的技术支持。同时,采取该仿真分析方式能大大节约试验成本及时间。
1 曹金凤,石亦平.ABAQUS有限元分析实例详解.北京:机械工业出版社,2009:98~108.
2 韦勇,裴磊,成艾国.基于ABAQUS的汽车覆盖件抗凹陷性分析.机电产品开发与创新,2010,23(1):80~82.
3 江海涛,康永林,王全礼,等.高强度汽车板的烘烤硬化特性.钢铁研究,2006:54~57.
4 刘展,祖景平,钱英莉,等.ABAQUS6.6基础教程与实例详解.北京:中国水利出版社,2008:324~328.
