汽油机正时链轮系统设计优化与动力学特性研究

刘功文 郝志勇 郑康 史来峰

（1.浙江大学；2.东风汽车公司技术中心）

1 前言

传统的齿形链传动为链片外侧直边齿廓与链轮直线齿廓啮合，存在多边形效应和啮入瞬间的冲击效应，使得齿形链链条的节距线与链轮的分度圆交替相割或相切[1]，链条中心线位置和从动链轮角速度呈周期性变化，导致啮入瞬间的冲击可加剧链条啮合力和链节内力[2]。因此，如何最大限度的削弱链轮多边形及冲击效应对系统稳定性及可靠性的影响是需要研究的重要内容之一。

冯增铭等研究了低转速下含内、外啮合特征的齿形链链板结构特征的动力特性分析[3]；张京正等模拟了传统直线齿廓与渐开线齿廓链轮在多刚体力学模型下啮合接触力和链条波动[2]；刘海蓉等采用简化的单个滚子与齿轮啮合进行静应力分析研究[4]。国外Zheng H等采用有限元模型研究了摩托车链轮的振动与噪声问题[5,6]；Nichol S.W等采用链条轨道减少冲击噪声[7]。目前对链轮传动的分析研究局限于静态或较低转速工况以及对单个链系统进行激励分析，同时对于多刚体力学模型则忽略了柔性体弹性变形对系统特性的影响，而有限元模型则存在网格划分繁琐及边界条件约束定义复杂等诸多问题。

本文建立了汽油机正时链传动系统动力学弹性模型，在不改变各链轮整体布置及导向板型线的情况下展开动力学优化，并对优化前、后的设计方案进行对比。

2 链轮链传动力学模型

由于存在链轮多边形效应，链节进入链轮的瞬间，链节与链轮齿以一定的相对速度啮合，链和链轮都受到冲击，并产生附加动载荷，且随着链轮转速的增加和链节距的加大而加剧，使传动产生振动和噪声。由链传动运动特性（图1）可知[8]:

式中，Ftq为主动链轮分度圆周上沿链条紧边方向的力（驱动力）；Ftz为从动轮链轮分度圆周上沿链条紧边方向的力 （阻力）；Tq为驱动力矩；Tz为阻力矩；R1为主动链轮分度圆半径；R2为从动链轮分度圆半径；x、y 为位置角，x 的变化范围是 x=-φ/2～φ/2（φ/2=π/Z1，Z1为主动链轮齿数），y 的变换范围是 y=-φ/2～φ/2（φ/2=π/Z2，Z2为从动链轮齿数）。

因此，链轮驱动力和阻力均近似呈余弦曲线波动，每过一个链节，链速就波动一次，瞬时传动比也随之变化。

同时，链条在与轮齿的啮入过程中也存在啮合冲击，冲击能量的大小与冲击速度有关。图2所示为链条与渐开线链轮的啮入冲击，链轮以角速度w旋转，B点为链节与齿面的接触点，当轮齿转动时对链节与齿面造成法向冲击，其速度大小为VB，用图解法可求得其为:

式中，xO2、yO2为O2点的坐标值，可计算得出；xB、yB为B点的坐标值。

3 链轮系统多体动力学模型建立

3.1 正时链轮系统参数

汽油机前端正时链轮传动系统由曲轴正时链轮、进/排气凸轮轴正时链轮、张紧导向板、固定导向板、上导向板及机械张紧器组成。针对原链轮设计方案存在啮合接触力大及角速度波动较大的问题，提出新设计方案，并建立虚拟样机进行CAE动态特性仿真对比分析。新、旧链轮系统设计方案的链节及链轮参数如表1所示。各链轮均为渐开线齿轮，链轮系统组成布置如图3所示。新设计方案在原方案基础上改动了链轮齿数、张紧器位置及链条类型，不影响前端凸轮轴、曲轴及各导向板的空间几何布置。

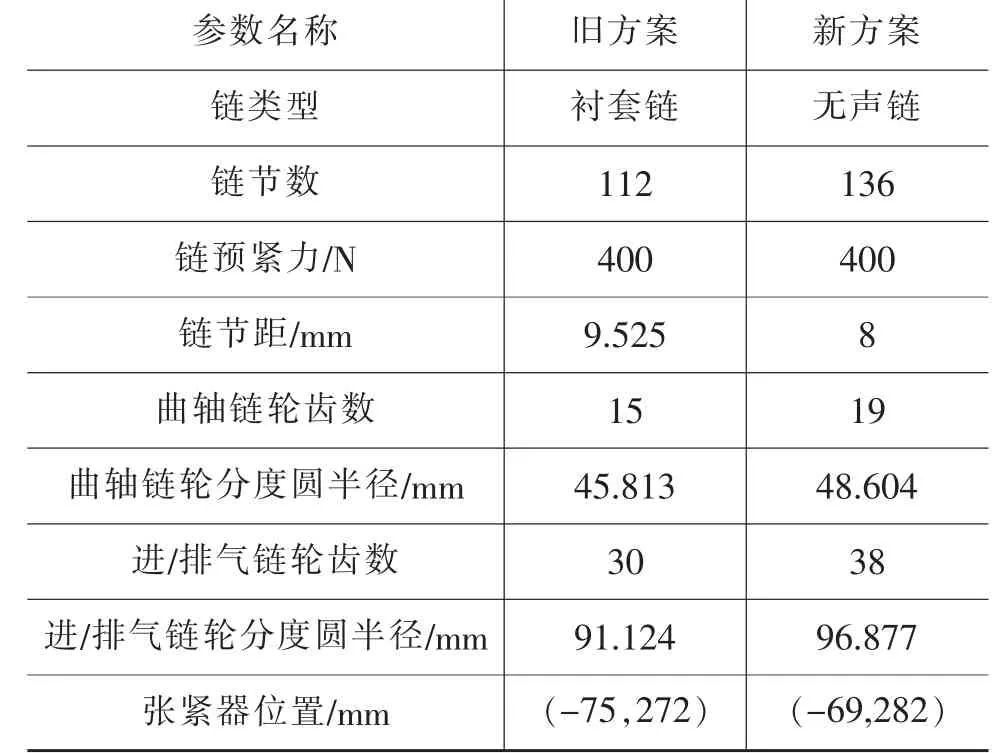
表1 新、旧方案的参数

3.2 多体动力学模型建立

多体动力学模型在Timing drive软件中建立，仿真模型如图4所示。模型分为两部分，一部分是正时链轮传动系统，包含曲轴链轮、进/排气凸轮轴链轮、张紧导向板及固定导向板等子结构；另一部分是进/排气多阀系部分，该部分主要是为了模拟配气机构的动力学特性，同时提供凸轮轴链轮的负载扭矩。

在张紧导向板处加入机械张紧力，力值常数为400 N。计算时多阀系考虑各凸轮轴沿各自轴线旋转和轴向平动，计入轴段径向轴承及止推轴承的弹性支承刚度，用非线性的弹簧阻尼来模拟。同时为实现链节与轮齿及导向板的接触与冲击，考虑了链轮齿及各导向板的轮廓。由于正时链轮系统主要是链节的啮合与冲击过程，因此模型中还考虑了链节间隙及使用摩擦因数，其数值常量为0.05。计算时采用该汽油机的额定转速6000 r/min。

3.3 曲轴转速波动

凸轮轴链轮与张紧导向板的负载施加如前所述。除了对曲轴链轮施加稳态转速激励外，同时还考虑曲轴前端的转速波动载荷。该机曲轴已经过优化，添加橡胶扭振减振器后，波动幅值有所衰减。

图5所示为优化后的曲轴前端在6000 r/min时的转速波动曲线，可以通过基于有限元的整机多体动力学PU模型计算得到[9]。图6为曲轴转速波动的频域曲线，可知前端转速波动的主要谐次为2、4、6等谐次，因为这些谐次在6000 r/min时引起了不同程度的扭振峰值，特别是第2谐次。

4 计算结果分析

4.1 链节接触冲击力对比分析

链节进入链传动系统子结构部分啮合点时会因速度波动产生一定程度的啮合冲击，不仅易导致零件磨损，还可能造成链条啮合脱离，产生噪声。

图7为旧方案仿真一个循环过程中链节经过各子结构时的接触冲击力。链节动态运动中过大的冲击和接触不均匀性易导致进入点的链节跳起及磨损。而由于曲轴链轮半径较小，相对角速度波动较大，因而链节经过曲轴链轮时的接触力最大，且峰值达到630 N，并存在多处受力为0的情况。同时，链节在经过上导向板时的接触力仅为一个峰值力凸起，不能起到良好的导向作用。

图8所示为新方案一个循环工况链节接触应力曲线。相较于图7，各处接触冲击力的幅值均有所下降，最大力仅为325 N，下降幅度达到48.4%，而且受力曲线波动较小，上导向板也起到了导向接触作用，改善了链节与各子结构的接触性能。

4.2 链轮角速度波动对比分析

取一个转速周期0.02～0.04 s为对比工况，进/排气凸轮轴链轮角速度比较结果如图9～图12所示。由图9和图11可知，时域下新方案的进、排气凸轮轴链轮的角速度曲线明显要优于原曲线，转动平稳，波动程度较小。

图10和图12反映的是链轮角速度快速傅里叶变换后的对比结果。可知旧方案的链轮角速度响应以第2、3.5、4、15及30阶次为主，其中前3个阶次主要由发动机固有基频特性产生（见图6）。而在19、30阶次附近的响应则主要是由链条多边形效应引起，为链轮齿数的整数倍。一般情况下为避免共振，曲轴链轮齿数应尽量选用质数且不能整除链节的数[10]，因而新方案增加至对应曲轴链轮齿数为19，凸轮轴链轮齿数为38。从新方案的频域结果可知，一方面在低频段的响应幅值相应有所削弱，另一方面在高频段的多边形频率以第19阶次为主，而更高阶次则受到阻尼的衰减。

由于激励载荷、间隙及链条刚度等因素的影响，链节的弹性变形将导致链轮的角速度波动，过大的波动将引起进、排气阀系的配气正时相位，对发动机的做功产生影响。

图13和图14为进气和排气链轮角速度之差（即角速度波动）的时域和频域比较结果。

由图13可知，旧方案的链轮角速度波动最大幅值可达到2.62 rad/s，而新方案的最大波动幅值仅为0.22 rad/s，角速度差别很小，可有效保证进/排气凸轮轴转动的同步性和平稳性。

由图14可知，旧方案的频域响应以第15、30、45阶次为主，这与链条多边形效应有关。而新方案的频域响应则以19、38阶次为主，且幅值要小很多，这除了与链轮齿数有关外，还与衬套链和无声链的啮合特性有关。相比于滚子/衬套链与链轮齿的无滑移啮合过程，无声链则是连续的滑移啮合（图15），因其链节轮廓与链轮齿廓的接触法线倾斜，可有效降低冲击速度，且连续滑移的啮合摩擦方式引起的啮合冲击阻尼也可降低多边形效应对链传动系统带来的波动程度。同时新方案中选用较小的链节节距使得啮合过程随时间变化较短，也对削弱多边形效应带来一定影响。

4.3 链节角速度对比分析

重新更改链条类型、链节数和链轮齿数，导致在一个链节循环工况下，进入各链轮的啮合时间要略早于旧方案（图16）。由图16可知，0.03～0.04s为链节与曲轴链轮啮合阶段，因曲轴链轮半径相对较小，所以此阶段的链节角速度略大。链节后续依次经过各个链传动的子结构，0.06～0.09s中间两个类矩形波谷表示经过排气及进气链轮时的角速度曲线。与旧方案相比，新方案的链节在进入各个链轮时的啮合冲击速度明显更平稳，曲线波动也较少，减少了一定的冲击力和磨损。

4.4 不考虑曲轴转速波动时的对比分析

采用同样的计算方法，不考虑曲轴转速波动，对新方案无声链系统计算链系统动态结果，并与前述计算结果比较。图17～图21反映了考虑与不考虑曲轴转速波动时，链轮角速度波动、链节角速度及链轮相对角速度波动的比较。

图17表明了曲轴转速波动对链节角速度的影响。可知两种情况计算的曲线几乎相近，因而曲轴转速波动对链节的角速度影响较小。

图18为排气凸轮轴链轮角速度时域比较。可知不考虑曲轴转速波动时凸轮轴链轮转速波动幅值较小，最大落差仅为2 rad/s，而且随着运行周期的延长，后期幅值越来越趋近于凸轮轴额定转速常数314 rad/s。考虑曲轴转速波动后，凸轮轴链轮转速波动幅度增大到了4.5 rad/s左右，相位也有所偏移。

图19为对应频域上的计算结果，不考虑曲轴转速波动时的动态响应阶次主要是第3.5阶次及19阶次，前者与发动机本身固有基频特性有关，后者则是由链轮的多边形效应产生。而考虑曲轴转速波动时的主要阶次为第2、3.5、4、19阶次，同时曲线中更多较小峰值则意味着更多高频分量的出现，其是由转速波动信号的谐次分量引起的。频域响应中引入曲轴角速度波动，一方面保留了链轮多边形频率的影响，另一方面则计入了发动机第2、第4阶次低频段的影响，最高峰值可达1.95 rad/s左右，与此同时整个频域段内发动机基频谐次对链轮角速度波动的影响要比多边形效应高频段明显。

同样情况也反映在链轮相对角速度波动的时域及频域计算结果中（图20和图21）。不同的是频域段的响应主要以第19、38阶次为主，而第2、4阶次的影响效果较小，说明链轮多边形效应对链轮相对角速度波动的影响效果要大于低频段发动机基频的影响。

5 结束语

通过应用多体动力学的方法对汽油机前端正时链轮传动系统的仿真分析，可以得出以下结论:

a.为避免链条和链轮磨损及共振，曲轴链轮齿数应选用质数且不能整除链节数，可有效改善链节与链轮的接触冲击。

b.无声链连续滑移的啮合方式比衬套链可以更有效降低啮合冲击速度以及多边形效应对链传动系统带来的波动程度。

c.曲轴前端的转速波动影响正时链轮的角速度及进/排气凸轮轴链轮相对角速度波动，且忽略转速波动影响的计算结果明显偏小振动，但对链节角速度及接触冲击力影响不大。

d. 凸轮轴链轮的角速度波动受低频段发动机基频谐次的影响较大，受链轮高频段多边形效应的影响因素较小，而链轮的相对角速度波动响应则相反。

e.链轮直径相同时，链节距小就会有更多的齿数参加啮合，因此采用小节距链节的方法可以有效减轻多边形效应，降低一定程度的磨损与冲击。

1 郑志峰，王义行，柴邦衡.链传动.北京:机械工业出版社，1984.

2 张京正，王勇，薛云娜.发动机正时链波动与冲击特性.山东大学学报（工学版），2007,37（2）:30～33.

3 冯增铭，孟繁忠，李纯涛，等.新型齿形链的啮合机制及仿真分析.上海交通大学学报，2005,39（9）:1427～1430.

4 刘海蓉，苪执元，鲁春明.冷却运输机滚子输送链的接触分析研究.计算机与数字工程，2007,35（3）:38～40.

5 Zheng H，Wang Y Y，Quek K P，et al.Investigation of meshing noise of roller chain drives for motorcyles.Noise Control Engineering Journal，2002,50（1）:5～11.

6 Zheng H，Wang K W，Havek S I，et al.Efficient modeling and prediction of meshing noise from chain drives.Journal of Sound and Vibration，2001,245（1）:133～150.

7 NICHOL S W.，FAWCETT J N.Reduction of Noise and Vibration in Roller Chain Drives.Proc.Mech.，Inst.London，Mech Engrs，1977:363～370.

8 徐跃进.链传动的动态特性.机械工程师，2007（6）:33～35.

9 段秀兵，郝志勇，岳东鹏,等.汽车发动机曲轴扭振的多体动力学分析.汽车工程，2005，25（2）:233～236.

10 蓝军.配气机构衬套链传动计算和结果评价.AVL年会论文，西安，2007.