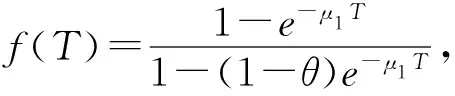一类对染病者实施连续接种和脉冲接种的时滞SIR传染病模型的比较

王桂臻，李必文，宣天赐，吴雪莹

(湖北师范学院 数学与统计学院，湖北 黄石 435002)

传染病对人类影响重大，每年都有成千上万人死于各种传染病.近年来，控制传染病已日益成为一个复杂问题，接种是根除传染病的一个重要策略.而脉冲接种传染病模型已经成为理论分析的主题.带有时滞的连续传染病模型已被广泛研究，最著名的时滞SIR传染病模型如下：

(1)

其中，S(t)，I(t)，R(t) 分别表示易感人群，染病人群，具有永久免疫的恢复人群在时间t的值，常数λ>0 表示移民率，假定所有的新生儿为易感人群.常数μi>0，i=1，2，3 分别表示易感人群，染病人群，恢复人群的死亡率.从生物学角度，很自然地假设μ1≤min{μ2，μ3}.常数β>0是接触率，常数γ>0是恢复率.非负常数h是离散时滞，表示个体成为染病者所需要的时间.

根据传统的接种疫苗策略，新生儿也应该接种疫苗，θ/T(0<θ< 1)是接种成功的比例.那么，上面的系统变为传统的实施连续接种策略的传染病模型

(2)

在原来的系统中考虑脉冲接种，我们可以建立下面的脉冲差分微分系统：

(3)

这里，参数0<θ<1 是接种成功的比例，脉冲接种每T年一次，n=0，1，2， ….

下面我们将分别对系统(2) 和(3) 的平衡点的性质进行研究，并得到脉冲系统持久性的条件，最后得到我们的主要结论.

1 连续接种的SIR模型

这一部分，我们将分别分析系统(2)的局部渐近稳定性.假定总人数N(t) 的变化由N*(t)=λ-μ1S(t)-μ2I(t)-μ3R(t) 决定，当t→∞ 时，N(t)→1 ，由于系统(2)的前两个方程不依赖于第三个方程，因此第三个方程可以省略.那么，系统(2)可以写成

(4)

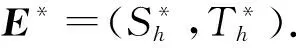
定义

(5)

定理1 若R0<1，则对于h≥0，系统(4)的无病平衡点E0=(λ/(μ1+(θ/T))，0) 是局部渐近稳定的.

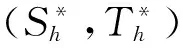
定理3 对于所有的ξ∈[-h，0) ，令系统(2)的初始条件S(ξ)=S(0)>0，I(ξ)=I(0)>0，R(0)>0，假设R0>1，那么如果满足

(6)

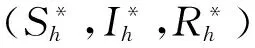
以上定理的证明与[1]类似，此处不再缀余.

2 带脉冲接种的SIR模型

在这部分，我们考虑每T年一次的脉冲接种的情形，其中，T是间隔脉冲时间，即两次连贯脉冲接种之间的时间.易感个体在脉冲接种以后将恢复，并得到疾病是否成为地方病的充分条件.显然，在系统(3)中，总人数接近1.为了方便起见，我们可以假设S(t)+I(t)+R(t)=1 .系统(3)的前两个方程不依赖于第三个方程.因此，我们只考虑下面的简化系统：

(7)

出于生物学意义，我们在闭集Ω上考虑系统(7).可以证明Ω关于系统(7)是正不变的.

2.1 无病周期解的全局吸引性

为了证明我们的主要结论，先给出下面的几个引理.

引理1[2]考虑下面的脉冲微分系统:

其中，a>0，b>0，0<θ<1. 则系统存在惟一的全局渐近稳定的正周期解

引理2[3](脉冲比较定理) 假设m∈PC[+，]在t=τk处间断， 且在t=τk满足左连续，k∈且

其中g∈C[+*+，] ，ψk∈C[，]，且Ψk(u) 对每个k∈关于u是非递减的.令ρ(t)是下面脉冲微分系统在[t0，∞]的最小解：

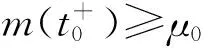
引理3[4]考虑下面的脉冲微分方程:

其中，a，b，ω都是正数，且x(t)>0，t∈[-ω，0) .则

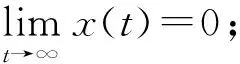
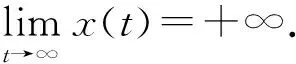
现在我们将证明无病平衡点(S*(t)，0) 是全局吸引的.首先，我们来说明无病平衡周期解的存在性，此时传染病个体为零，即I(t)=0，t>0.在这个假设下，易感人群的增长率必须满足

(8)

根据引理1，我们知道系统(8)的周期解

是全局渐近稳定的.因此，系统(7)有一个无病周期解 (S*(t)，0).

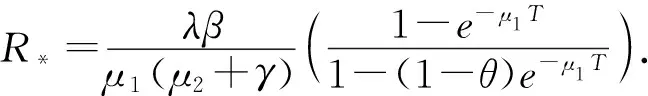
定理4 若R*<1 ，那么系统(7)的无病周期解(S*(t)，0) 是全局吸引的.

证明 由于R*<1，我们可以选取足够小的ε>0，满足

(9)

由(7)的第一个方程，我们有S′(t)<λ-μ1S(t) ，下面我们考虑脉冲比较系统：

(10)

由引理1，得到系统(10)的周期解，即

根据脉冲比较定理，存在m1∈+，使得S(t)≤x(t)

(11)

进一步地，由第二个方程，我们有

考虑下面的脉冲比较系统：

(12)

由引理1，得到系统(12)的周期解

根据比较定理，存在一个整数m3>m2， 使得

S(t)≥z(t)>z*(t)-ε1，nTm3

(13)

由于ε和ε1都是充分小的，由(11)和(13)知

S*(t)-ε

因此，系统(7)的无病周期解(S*(t)，0) 是全局吸引的.证毕.

3 连续和脉冲接种的比较

[1]Pei Yong-zhen，Li Shu-ping，Li Chang-guo，et al.The effect of constant and pulse vaccination on an SIR epidemic model with infectious period[J].Applied Mathematical Modelling， 2011，35:3866～3878.

[2]Gao S， Chen L， Teng Z. Impulsive vaccination of an SEIRS model with time delay and varying total population size[J].Bull Math Biol，2007，69(1):731～745.

[3]Zang Shu-wen， Wang Fen-yan， Chen Lan-sun. A food chain system with density-dependent birth rate and impulsive perturbations[J]. Advances in Com-plex Systems， 2006， 9(3): 1～14.

[4]Yang Kuang.Delay Differential Equations with Applications in Population Dynamics[M].San Diego:Academic Press( INC)，1993.

[5]Masaki Sekiguchi，Emiko Ishiwata.Dynamics of a discretized SIR epidemic model with pulse vaccination and time delay[J].Journal of Computational and Applied Mathematics，2011，236(6):997～1008.

[6]Li Biwen，Xiong Xinsheng.Existence and global attractivity of periodic solution for a discrete pry-predator model with sex structure[J].Nonlinear Analysis:Real World Applications，2010，11:1986～2000.

[7] 李必文，杜 漫，万素梅.一个病毒传染模型的稳定性[J].湖北师范学院学报(自然科学版)，2005，25(4): 8～10.

[8]章培军，李维德，朱凌峰.SIRS传染病模型的连续接种和脉冲接种的比较[J].兰州大学学报(自然科学版)，2011，47(1):82～86.