广义度量空间弱压缩映像下的不动点定理

刘 博，柴国庆

(湖北师范学院 数学与统计学院，湖北 黄石 435002)

1 引言及预备知识

Branciari[1]在2000年将原有的三角不等式中右端的两项扩展为了三项，推广了之前的度量空间，得到了广义度量空间.并且在引入Hausdorff概念之后，证明了在广义度量空间之中Banach压缩原理依然成立.之后很多学者在这个空间之中进行了一系列的研究， 参照文献[3～8].

在文献[2]中， 作者在具有Hausdorff性质的广义度量空间中，引入了一种推广的Banach压缩条件.本文主要是针对文献[2]进行推广，去掉原来条件中φ-函数的连续性，并且把原有弱压缩条件中的元素由一个推广为三个，我们的结果改进了原有结果.

定义1[1]X是一个非空集，映射d:X×X→[0，+∞)，使得对于所有的x，y∈X以及对于不同于x，y的所有相异的u，v∈X点 ，有：

i)d(x，y)=0 当且仅当x=y，

ii)d(x，y)=d(y，x) ，

iii)d(x，y)≤d(x，u)+d(u，v)+d(v，y) .

则称(X，d) 为广义度量空间.

定义2[1](X，d) 是广义度量空间， {xn}是X中的一个序列，并且存在x∈X.在广义度量空间中称 {xn}收敛到x，当且仅当n→+∞ 时d(xn，x)→0；记为xn→x.

定义3[1](X，d) 是广义度量空间， {xn}是X中的一个序列.称{xn} 为广义度量空间中的柯西列，当且仅当对于任意的ε>0，存在一个自然数N(ε) ，使得当n>m>N(ε)时，d(xn，xm)<ε.

定义4[1](X，d) 是广义度量空间，若对于X中任意的柯西列都收敛到X，则称 (X，d)是完备的广义度量空间.

最近，Lakzian[2]引入了以下的定义：

定义5[2]令集合Ψ是函数ψ:[0，+∞) →[0，+∞)的全体所组成的集合，其中ψ满足：

i)ψ连续非减， ii)ψ(t)=0当且仅当t=0.

定义6[2]令集合Φ是函数φ:[0，+∞)→[0，+∞) 的全体所组成的集合，其中φ满足：

i)φ连续， ii)φ(t)=0当且仅当t=0 .

同时，他们获得了下面的不动点结果：

定理1[2](X，d) 是Hausdorff的完备广义度量空间，自映射T:X→X，若对于所有的x，y∈X，满足条件：

ψ(d(Tx，Ty))≤ψ(d(x，y))-φ(d(x，y))

其中ψ∈Ψ，φ∈Φ，则T有唯一的不动点.

2 主要结果

我们首先给出如下的定义.

定义7 令集合Θ是函数θ的全体所组成的集合，其中θ:[0，+∞)→[0，+∞) 满足：

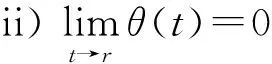
现在给出我们的结果.

定理2 (X，d) 是Hausdorff的完备广义度量空间，自映射T:X→X，若对于所有的x，y∈X，满足条件：

ψ(d(Tx，Ty))≤ψ(a1d(x，y)+a2d(x，Tx)+a3d(y，Ty))-

θ(a1d(x，y)+a2d(x，Tx)+a3d(y，Ty))

(1)

其中a1+a2+a3≤1，ai≥0(i=1，2，3)，并且ψ∈Ψ，θ∈Θ，则T有唯一的不动点.

证明 取任意的x0∈X，定义序列{xn} ，其中

xn+1=Txn

(2)

先证明d(xn，xn+1)→0.利用(1)，有

ψ(d(xn，xn+1))=ψ(d(Txn-1，Txn))≤

ψ(a1d(xn-1，xn)+a2d(xn-1，Txn-1)+a3d(xn，Txn))-

θ(a1d(xn-1，xn)+a2d(xn-1，Txn-1)+a3d(xn，Txn))≤

ψ(a1d(xn-1，xn)+a2d(xn-1，Txn-1)+a3d(xn，Txn))=

ψ(a1d(xn-1，xn)+a2d(xn-1，xn)+a3d(xn，xn+1))

(3)

因为ψ连续非减，故

d(xn，xn+1)≤a1d(xn-1，xn)+a2d(xn-1，xn)+a3d(xn-1，xn)

即

(1-a3)d(xn，xn+1)≤(a1+a2)d(xn-1，xn)

(4)

因为d(xn，xn+1)=d(xn+1，xn)，而

ψ(d(xn+1，xn))=ψ(d(Txn，Txn-1))≤

ψ(a1d(xn，xn-1)+a2d(xn，Txn)+a3d(xn-1，Txn-1))-

θ(a1d(xn，xn-1)+a2d(xn，Txn)+a3d(xn-1，Txn-1))≤

ψ(a1d(xn，xn-1)+a2d(xn，Txn)+a3d(xn-1，Txn-1))=

ψ(a1d(xn，xn-1)+a2d(xn，xn+1)+a3d(xn-1，xn))

(5)

因为ψ连续非减，所以

d(xn+1，xn)≤a1d(xn-1，xn)+a2d(xn，xn+1)+a3d(xn-1，xn)

即

(1-a2)d(xn，xn+1)≤(a1+a3)d(xn-1，xn)

(6)

由(4)，(6)知

(2-a2-a3)d(xn，xn+1)≤(2a1+a2+a3)d(xn-1，xn)

(7)

不妨假设r>0，若a1=a2=a3=0，由(3)知ψ(d(xn，xn+1))≤0 ，又因为ψ(d(xn，xn+1))≥0 ，因此ψ(d(xn，xn+1))=0，即r=0，矛盾.

若a1+a2+a3>0，则

因此

(8)

由(3)知，

ψ(d(xn，xn+1))≤ψ(a1d(xn-1，xn)+a2d(xn-1，xn)+a3d(xn，xn+1))

-θ(a1d(xn-1，xn)+a2d(xn-1，xn)+a3d(xn，xn+1))

应用(7)，(8)对其求极限有

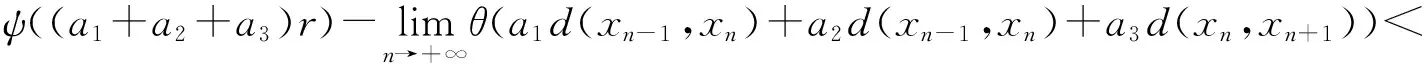
ψ((a1+a2+a3)r)≤ψ(r)

即ψ(r)<ψ(r)，矛盾. 因此假设不成立，即

(9)

同理可证

(10)

再次，我们证明T有周期点.

假设不成立，即T没有周期点，则序列{xn} 中任意不同两点相异，即：当n≠m时xn≠xm.

d(xni，xmi)≥ε

(11)

固定mi，由(9)，(10)知，可以取到满足(11)的最小的ni，使得

d(xni-1，xmi)<ε

(12)

因此由(11)，(12)有

ε≤d(xni，xmi)≤

d(xni，xni-2)+d(xni-1，xni-2)+d(xni-1，xmi)<

d(xni，xni-2)+d(xni-1，xni-2)+ε

利用(9)，(10)对上式求极限，知

(13)

另一方面，因为

d(xni，xmi)≤d(xni，xni-1)+d(xmi，xmi-1)+d(xni-1，xmi-1)

d(xni-1，xmi-1)≤d(xni，xni-1)+d(xmi，xmi-1)+d(xni，xmi)

应用(9)，(13)对其求极限，知

(14)

由条件(1)知

ψ(d(xni，xmi))=ψ(d(Txni-1，Txmi-1))≤

ψ(a1d(xni-1，xmi-1)+a2d(xni-1，xni)+a3d(xmi-1，xmi))-

θ(a1d(xni-1，xmi-1)+a2d(xni-1，xni)+a3d(xmi-1，xmi))

(15)

若a1=0，利用(9)，(14)，则有

(16)

利用(13)，(16)对(15)两边求极限，有ψ(ε)≤0，又因为ψ(ε)≥ 0，因此ψ(ε)=0，即ε=0，矛盾.

若a1>0，利用(9)，(14)，则有

(17)

利用(13)，(17)对(15)两边求极限，则有

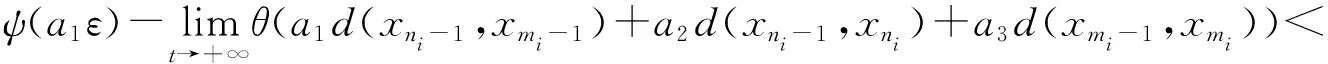
ψ(a1ε)≤ψ(ε)

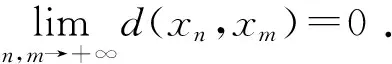
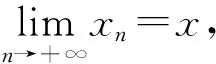
(18)

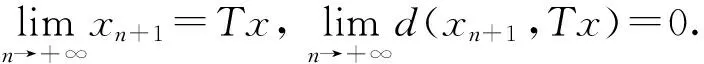
ψ(d(xn+1，Tx))=ψ(d(Txn，Tx))≤

ψ(a1d(xn，x)+a2d(xn，Txn)+a3d(x，Tx))-

θ(a1d(xn，x)+a2d(xn，Txn)+a3d(x，Tx))≤

ψ(a1d(xn，x)+a2d(xn，Txn)+a3d(x，Tx))

因为ψ连续非减，因此有

d(xn+1，Tx)≤a1d(xn，x)+a2d(xn，Txn)+a3d(x，Tx)≤

a1d(xn，x)+a2d(xn，xn+1)+a3d(x，xn)+a3d(xn，xn+1)+a3d(xn+1，Tx)

即

(1-a3)d(xn+1，Tx)≤(a1+a2)d(xn，x)+(a2+a3)d(xn，xn+1)

(19)

同理

(1-a3)d(Tx，xn+1)≤(a1+a2)d(xn，x)+(a2+a3)d(xn，xn+1)

(20)

因此由(19)，(20)和2-a2-a3>0 有

(21)

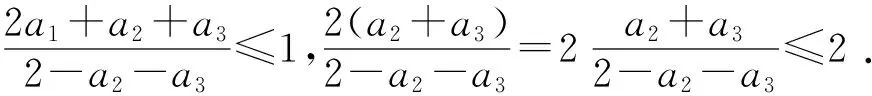
对(21)两边求极限知

因为(X，d) 是Hausdorff的，因此

Tx=x

这与T没有周期点的假设矛盾.因此T具有周期点，即存在u∈X，p≥1，使得

u=Tpu.

(22)

最后证明不动点的存在性和唯一性.

i) 存在性：若p=1，则u=Tu，即u就是所求不动点.

若p>1，我们可以证明b=Tp-1u为所求不动点，假设它不是不动点，则d(Tp-1u，Tpu)>0 .

ψ(d(u，Tu))=ψ(d(Tpu，Tp+1u))=ψ(d(T(Tp-1u)，T(Tpu)))≤

ψ(a1d(Tp-1u，Tpu)+a2d(Tp-1u，Tpu)+a3d(Tpu，Tp+1u))-

θ(a1d(Tp-1u，Tpu)+a2d(Tp-1u，Tpu)+a3d(Tpu，Tp+1u))

(23)

若a1=a2=a3=0，则d(u，Tu)=0，即u=Tu，这与p>1 矛盾.

若a1+a2+a3>0，因为d(u，Tu)>0，d(Tp-1u，Tpu)>0，知

θ(a1d(Tp-1u，Tpu)+a2d(Tp-1u，Tpu)+a3d(Tpu，Tp+1u))>0

由此应用(23)，以及ψ的性质易得

(1-a3)d(u，Tu)<(a1+a2)d(Tp-1u，Tpu)

(24)

同理

(1-a2)d(u，Tu)<(a1+a3)d(Tp-1u，Tpu)

(25)

因此由(24)，(25)我们有

(26)

同理，易证d(Tp-1u，Tpu)≤d(Tp-2u，Tp-1u)

如此进行下去，得到

d(u，Tu)

即d(u，Tu)

因此假设不成立，即b=Tp-1u为不动点.

ii) 唯一性：若存在两个不动点s，t∈X，且s≠t，则

ψ(d(s，t))=ψ(d(Ts，Tt))≤

ψ(a1d(s，t)+a2d(s，Ts)+a3d(t，Tt))-θ(a1d(s，t)+a2d(s，Ts)+a3d(t，Tt))=

ψ(a1d(s，t))-θ(a1d(s，t))

若a1=0，则ψ(d(s，t))=0，即d(s，t)=0，则s=t，矛盾.

若a1>0，不妨假设d(s，t)≠0，则有

ψ(d(s，t))≤ψ(a1d(s，t))-θ(a1d(s，t))<ψ(a1d(s，t))≤ψ(d(s，t))

矛盾. 因此假设不成立，所以d(s，t)=0，即T具有唯一不动点.

推论1 设(X，d) 是具有Hausdorff性质的完备广义度量空间，自映射T:X→X，若对于所有的

x，y∈X，满足条件：

ψ(d(Tx，Ty))≤ψ(d(x，y))-θ(d(x，y))

其中，ψ∈Ψ，θ∈Θ， 则T有唯一的不动点.

推论2 (X，d) 是Hausdorff的完备广义度量空间，自映射T:X→X，若对于所有的x，y∈X，满足条件：

ψ(d(Tx，Ty))≤ψ(a1d(x，y)+a2d(x，Tx)+a3d(y，Ty))-φ(a1d(x，y)+a2d(x，Tx)+a3d(y，Ty))

其中a1+a2+a3≤1，ai>0(i=1，2，3)，并且ψ∈Ψ，φ∈Φ，则T有唯一的不动点.

注： 显然推论1和推论2是定理1的推广.

[1]Branciari A. A fixed point theorem of Banach-Caccioppoli type on a class of generalized metric paces[J].Publ Math Debrecen，2000，57:31～37.

[2]Lakzian H. Fixed points for weakly contractive mappings in generalized metric spaces[J]. Appl Math Lett，2012，25:902～906.

[3]Azam A，Arshad M.Kannan fixed point theorem on generalized metric spaces[J].J Nonlinear Sci Appl，20081:45～48

[4]Das P. A fixed point theorem on a class of generalized metric spaces[J].Korean J Math Sci，2002，9: 29～33.

[5]Sarma I R， Rao J M， Rao S S.Contractions over generalized metric spaces[J].J Nonlinear Sci Appl，2009，2(3)：180～182.

[6]Mihet D.On Kannan fixed point principle in generalized metric spaces[J].J Nonlinear Sci Appl，2009，2(2):92～96.

[7]Fora A， Bellour A， Al-Bsoul A.Some results in fixed point theory concerning generalized metric spaces[J].Mat Vesnik， 2009，61(3):203～208.

[8]Akram M， Siddiqui Akhlaq A. A fixed-point theorem for A-contractions on a class of generalized metric spaces[J].Korean J Math Sci， 2003，10(2): 1～5.