色谱经济分析法系列研究:分离度理论
2013-09-03任静儒陈安琪程佳朦
沈 萍,任静儒,陈安琪,程佳朦
(1.武汉职业技术学院,武汉430074;2.武汉大学经济与管理学院,武汉 430072)
色谱经济分析法系列研究:分离度理论
沈 萍1,任静儒2,陈安琪2,程佳朦2
(1.武汉职业技术学院,武汉430074;2.武汉大学经济与管理学院,武汉 430072)
将化学色谱分析法引入到经济学中对复杂经济现象进行分类分析,先后已进行了平衡理论、塔板理论和速率理论等系列置换研究。在这些研究的基础上,文章将探讨色谱经济分析法的重要理论:分离度理论,进一步研究色谱柱对复杂经济现象分离效果的量度指标,探讨提高色谱柱分离效果的方法,并为后续经济信号检测、定性定量分析的研究作好一定的铺垫。
色谱经济分析法;分离度理论;柱效能
0 引言
游士兵等(2011~2013)前期将化学色谱分析法引入到经济学研究领域进行了初步探索和研究,完成了创建色谱经济分析法的有关基础研究、塔板理论置换研究、速率理论的置换模拟及其经济学思考,在前期研究成果中已经说明了分配比的差异是组分分离的本质原因(沈萍等,2011),而分配比的差异可通过保留时间的不同来体现,而色谱峰扩宽的程度也影响着色谱柱的分离效果,因此,本文将在前期研究的基础上进一步研究色谱柱对复杂经济现象分离效果的量度指标,探索色谱经济分析法在社会科学领域中的实际应用价值,并为下一步探讨提高色谱柱分离效果的方法打下一定的理论基础。
1 化学色谱分析法分离度理论主要量度指标
1.1 色谱柱效能
在化学领域色谱柱的效能通常用有效塔板数neff来表达,当两组分经过色谱柱的检测,得到色谱图后即可测定调整保留时间(tR’)、峰宽(W)以及半峰宽(Wh/2),如图1所示:

图1 混合两组分经过色谱柱检测的色谱图
其中,tRM为空气流出色谱柱的保留时间,tR1为组分1流出色谱柱的保留时间,tR2为组分2流出色谱柱的保留时间,tR1’为组分1流出色谱柱的调整保留时间,即tR1’=tR1-tRM,同理,tR2’为组分2流出色谱柱的调整保留时间,即tR2’=tR2-tRM;W1为组分1流出色谱柱的峰宽,W2为组分2流出色谱柱的峰宽,在峰高为一半时峰宽即为半峰宽(Wh/2)。
有效塔板数与色谱参数之间的关系为:

其中tR’为调整保留时间,W为色谱峰的峰宽,Wh/2为色谱峰的半峰宽,此时峰宽(W)及半峰宽(Wh/2)的单位用时间表示。进而可以由上式(1)计算出该色谱柱的有效塔板数。
应该注意的是,不同组分经过同一色谱柱后的色谱峰是不同的,即不同组分的tR、W和Wh/2不同,所计算出的n不同,即同一色谱柱在分离不同组分的混合物时,同一色谱柱对不同组分的柱效能是不同的。因此,当测定色谱柱的有效塔板数时,应说明是用什么物质进行测定的有效塔板数。
1.2 分离度(R)
色谱柱的有效塔板数越大,表示组分在色谱柱中达到分配平衡的次数越多,固定相的作用越显著,因而对分离越有利。值得指出的是,用塔板理论所表示的柱效不能表示被分离组分的实际分离效果,因为分离的可能性取决于待分离的混合物中不同组分分配比的差异大小,而不是取决于分配平衡的次数的多少,当不同组分的分配比都相同时,无论该色谱柱的塔板数多大,都无法分离。因此,不能将有效塔板数看作能否实现混合物中不同组分分离的依据,只能将有效塔板数和理论塔板高度看作在一定条件下色谱柱分离能力发挥程度的标志。
分配比反映了色谱柱对物质保留值的差别,它决定了不同组分经过色谱柱分离后的保留时间的差距;而色谱柱的柱效能反映的是色谱峰扩宽的程度,但都不能表示色谱柱的总分离效能,为了综合考虑保留值的差值和峰宽对分离的影响,测定色谱分离中所达到的分离程度,需要引入分离度的概念。
分离度又称为分辨率,定义为两个相邻组分的保留值之差与其平均峰宽值之比,用R表示,其表达式为:

当R<0.8时,两组分不能完全分离
当0.8<R<1时,两峰部分重叠,两组分分离程度低;
当R=1时,两峰重叠约2%,两组分分离的程度可以达到98%;
当R=1.5时,两组分分离的程度可以达到99.7%,通常R=1.5作为相邻两组分完全分离的指标。
2 色谱经济分析法分离度理论应用模拟
在《色谱经济分析法中保留时间的置换研究》(沈萍、游士兵等2013)一文中已经以上市公司的分红行为为研究对象,对保留时间进行置换。在中国金融市场上,上市公司分红在一定程度上是选择性的行为。参照化学领域的色谱塔板理论,以下将对分离不同类型上市公司的分离过程进行假设。
假设1:在一批同类上市公司群中有许多相互独立的公司,在每个时期所有公司均获得净利润,并且这些公司在除去法定公积金和法定公益金后,仍存在可供股东分配的利润,即满足分红的条件。同时,在这些上市公司中,每个时期都存在分红和不分红的公司。
假设2:假定固定相设置为公司的利润留存倾向,将流动相设置为公司的利润分红倾向。当一批同类上市公司群随脉冲式流动相进入色谱柱后,每个时期(t)选择分红的公司数量与选择不分红的公司数量的比值为定值,该定值即为该类型上市公司群的分配比(k’)。
假设3:假设利润充当载气的角色,是推动企业进行分红的内在机制。由于利润并不是连续实现的,而是呈脉冲式逐期流经不同的部门,这种表现形式与化学领域中载气的特性是统一的。由于上市公司选择进行分红的时期数一般不超过2次,所以将上市公司选择进行分红的时期数进行信号放大处理后设定为有效塔板数,即假设有效塔板数为上市公司选择进行分红的时期数的1000倍。
假设4:色谱经济分析法对经济领域的保留时间定义为:主体开始作用到其特定指标变化出现出样峰值所需要的时间(tR)。需要说明的是:第一,“指标”的选取需要依据组分特定情况的分离目的而定,但其最优选择能达到推断内部机制,实现有效分离的目的;第二,这里的“时间”不仅仅是通常意义上的时间概念,是扩充经济领域中的具体因素或变量。
假设5:假定有A、B和C三种不同类型的上市混合公司群,其中A和B两种不同类型上市公司群在固定相与流动相间的分配比不同,而C类上市公司的特点是在获得可供股东分配的利润,具备向股东分配红利的条件时,但在对A和B两种不同类型上市公司的混合群进行色谱分离时,C类上市公司还未对本公司股东分配的利润做出分配或留存决议,即C类上市公司在固定相与流动相间不分配,我们把C类上市公司称为分离过程中不被色谱柱保留的其他干扰组分。
当A、B和C三种不同类型上市混合公司群通过色谱柱时,C类上市公司不会在色谱柱内的固定相与流动相之间进行分配,而是直接穿过色谱柱,从出口流出色谱柱,但A和B两种不同类型上市公司群通过色谱柱时,会在色谱柱内的固定相与流动相之间进行分配,并且达到平衡,当混合组分穿过色谱柱,由于不同组分在固定相与流动相之间进行分配比存在差异,若干次的分配平衡会放大这种差异,使得A和B两类上市公司群在不同的时间从色谱柱的出口流出,即不同的组分会有不同的流出时间——保留时间。
假定混合样本中每种组分的初始数都为一个单位,当混合样本进入色谱柱后,经过色谱柱的分离后可得到色谱图,见图2。其中,A和B两种不同类型上市公司群的保留时间分别为:tRA为16.40;tRB为17.63;其峰宽分别为:WA为1.11;WB为1.21,另外,不被色谱柱保留的其他干扰组分——C类上市公司的保留时间tRM为1.30。
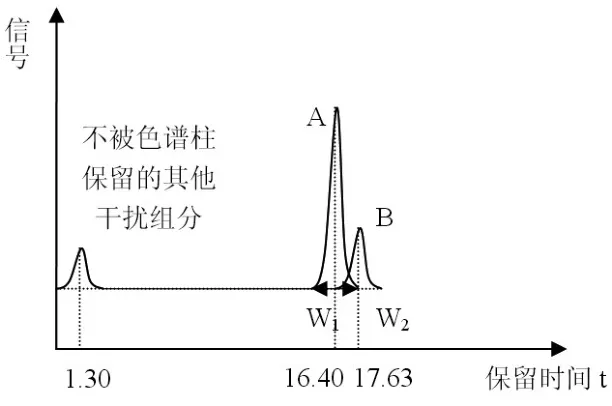
图2 A和B两种不同类型混合上市公司群的分离色谱图
那么,可以通过对色谱柱的分离结果的分析解决以下问题:
问题1:此次分离过程中A和B两种不同类型上市公司群经历了多少次的分配?即色谱柱的有效塔板数是多少?
问题2:此次分离的效果如何,分离度为多少?
问题3:此次A和B两种不同类型上市公司群的分离过程中,分配比为每时期选择分红的公司数量与选择不分红的公司数量之比,那么每类上市公司群的分配比为多少?
问题4:若以R=1.5(即分离程度达到99.7%)作为相邻两组分完全分离的指标,那么A和B两种不同类型上市公司群需要经历多少次的分配才能实现混合成分的完全分离,即色谱柱的有效塔板数是多少时才能实现混合成分的完全分离?
首先,根据公式(1)可得上市公司A与B混合样本的在该次分离中有效塔板数,此次分离中A类上市公司群的有效塔板数为:
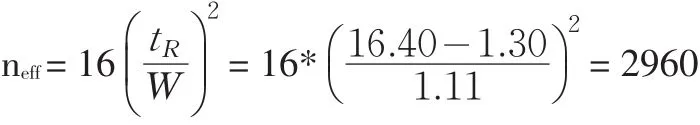
此次分离中B类上市公司群的有效塔板数为:
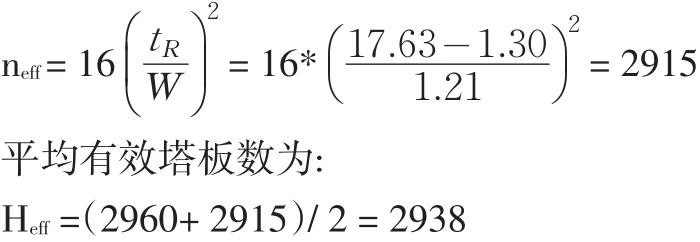
可见,此次分离过程中A和B两种不同类型上市公司群经历了2938次的分配平衡,色谱柱的有效塔板数是2938,此次分离的柱效为2938,即在柱口检验的指标为恰好进行了2.938次分红。有效塔板数只能反映色谱柱分离能力发挥程度的大小和色谱峰扩宽的程度,并不能完全反映分离程度的大小,即不能完全反映色谱柱的总分离效能,而分离度能够综合考量不同组分经过色谱柱分离后的保留时间的差距,以及峰宽对分离的影响,准确反映色谱分离中所达到的分离程度。
那么,根据公式(1)可得A和B两种不同类型上市公司群的混合样本的分离度的大小:
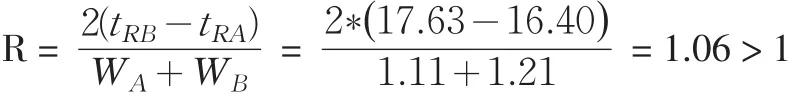
由于,当R=1时,两峰重叠约2%,两组分分离的程度可以达到98%;根据以上计算结果可知该次分离的分离度达到了1.06,其平均塔板数为3445,即此次分离过程中A和B两种不同类型上市公司群进行了3.445次的分红,所得到的两个色谱峰重叠小于2%,分离的程度可以大于98%,基本实现完全分离。
在《色谱经济分析法置换系列研究:分配比》(沈萍、游士兵等2011)一文中已经对色谱经济分析法中分配比进行了置换研究,在经济学领域中,分配比是固定相对组分的作用与流动相对组分的作用的比值,利用固定相、流动相对组分的作用差别,让组分在固定相、流动相中反复作用,不同组分在固定相和流动相中的差异逐渐累积,使不同组分逐渐分离,最终达到分离的效果。所以,在经济学领域中分配比定义为在一定的经济环境下,所选取的固定相和流动相对于被分离组分的作用大小之比,与化学领域中的分配比不同的是,经济学领域中的分配比不再只是某一个确定因素在固定相和流动相作用下的比例,而是根据所要分析的具体问题来定,但分配比与保留时间之间有以下关系:

由此可见,此次A和B两种不同类型上市公司群的分离过程中,A类型上市公司群每个时期(t)选择分红的公司数量与选择利润留存不分红的公司数量的比值为11.62;B类型上市公司群每个时期(t)选择分红的公司数量与选择利润留存不分红的公司数量的比值为12.56,两者的分配比差为0.94。
在经济分析中,有一些组分的分配比我们是已知的,如通过具体的实践调查所得,但是将这些经济行为或者经济主体混在一起时,我们只知道其中存在着哪一些的分配比,这时任务便是将不同分配比的组分分离出来;有一些组分的分配比是未知的,可通过分离的结果计算出相应的分配比,不同的分配结果是不同的分配比作用的结果。在我们进行一次或者多次试探性实验后,可以得到相应的客观经验,形成较稳定的体系,从而促进进一步实践完全分离。
对于两者的分配比差为0.94的A和B两种不同类型上市公司群的混合样本,要经历多少次分配才能实现混合成分的完全分离(以R=1.5为标准)?如果混合物中两个不同组分的分配系数相差无几,我们称这两个不同组分为最难分离物质对,因为其分配比差距太小,故有:K1≈K2≈ K ;W1≈ W2≈ W,根据公式(1)和(2)可得(4):

对于包括A和B两种不同类型上市公司群的混合样本,如果将有效塔板数(混合样本在固定相和流动相之间经历的分配次数)由2938增加到5883,即混合样本的分红次数由2.938增加到5.883,就可以实现混合成分99.7%,即R=1.5的完全分离。可见,分离度的指标不仅可以反映色谱柱的分离效果,还可以指导实际的分离工作,提高分离效果,甚至实现完全分离的效果。
3 色谱经济分析法分离度理论应用模拟思考
在经济学领域应用色谱经济分析法对复杂经济现象进行分离时,可以用有效塔板数来衡量在一定条件下色谱柱分离能力发挥程度,而分离度是色谱分离中所达到的分离程度的标志,为进一步探讨影响复杂经济现象的混合样本的有效分离的因素,需引入选择性这个概念。选择性是指固定相对两个相邻组分的调整保留值之比,用r21表示,又称为相对保留值,r21越大,表明待分离的混合组分的保留时间的差距越大,那么经过色谱柱的分离后,两组分的色谱峰的间距就越大,越容易实现完全分离。

综合公式(1)、(2)、(3)和(5)可得:

可见,分离度R与柱效neff、色谱柱的选择性r21有关,另外,待分离的混合组分的在固定相与流动相之间的分配比的差异大小,是能否实现完全分离的决定性因素。
3.1 分离度与柱效的关系
由公式(6)可知:R与 n成正比,n增加到原来的两倍,R只增加到原来的1.4倍,尽管如此,增加组分在色谱柱中达到分配平衡的次数,即增加有效塔板数,提高柱效是提高分离度的最直接、最简单,也是最有效的手段之一,但增加组分在色谱柱中达到分配平衡的次数,同时意味着组分的保留时间也会增加。如果想通过增加有效塔板数实现提高分离度的目的,就需要更多的分离时间,当我们需要对复杂经济现象进行快速完全的分离,那么通过增加有效塔板数来提高分离度就不是最理想的方法。
3.2 分离度与选择性的关系
r21是色谱柱的选择性的量度指标,r21越大,表明色谱柱的选择性越好,分离的效果就越好。根据公式(6)可计算出在给定的r21值下,获得所需要分离度对色谱柱的有效塔板数的要求,见下表1:

表1 在给定的r21值下,获得所需要分离度对色谱柱的有效塔板数的要求
由表1可知:当r21值为1时,分离所需要的有效塔板数为无穷大,即不能实现混合样品的完全分离。r21值越大,达到相同分离度所需要的有效塔板数越小,即越容易分离。当r21值为1.25时,要获得分离度R为1的分离效果,有效塔板数只要400,即复杂的混合样品在色谱柱中经过400次分配平衡即可达到R为1的分离效果;当r21值为1.5时,要获得分离度R为1的分离效果,只要复杂的混合样品在色谱柱中经过140次分配平衡即可,或者复杂的混合样品在色谱柱中经过320次分配平衡即可达到R为1.5的完全分离的效果。
可见,增加色谱柱选择性是提高分离度的有效办法。
实际分离过程中,增加r21值的有效方法就是改变固定相,使得固定相对复杂经济现象中不同的待分离组分的作用差距增加,即不同的待分离组分在固定相与流动相之间的分配比差距越大,如上市公司对法定公积金和法定公益金额度的调整等变动而改变了分配北,复杂的混合样品在经过色谱柱时,复杂的混合样品不断地在固定相与流动相之间进行分配并达到平衡,待分离组分在固定相、流动相中反复作用,逐渐累积其在固定相和流动相中的差异,使不同组分逐渐分离,最终达到分离的效果。不同的待分离组分在固定相与流动相之间的分配比差距越大,达到相同分离度所需要的有效塔板数越小,即越容易分离,分离效果越好。
在上述应用模拟实例中,研究对象为不同类型混合上市公司群的分红行为,对应的选择性r21是指固定相对两个相邻组分的调整保留值之比:
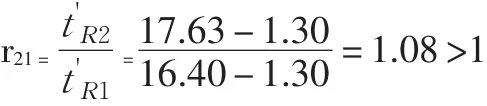
r21值为1.08,由以上分析可知,此次A和B两种不同类型上市公司群的混合样本可以实现完全分离。混合样本在固定相和流动相之间经历5883次的分配,即分离的有效塔板数达到5883,就可以实现混合成分99.7%,即R=1.5的完全分离。
3.3 分离度与分配比的关系
在经济学领域中,对复杂经济现象绩效色谱分离时,分配比是固定相对组分的作用与流动相对组分的作用的比值,即经济分配比的定义为;在一定的经济环境下,所选取的固定相和流动相对于被分离组分的作用大小之比利用固定相、流动相对混合样本中不同的组分的作用差别,让不同的组分在固定相、流动相中反复作用,不同组分在固定相、流动相中的差异逐渐累积,使不同组分逐渐分离,最终达到分离的效果。

另外,由《色谱经济分析法置换系列研究:塔板理论》(游士兵等2012)可知:

其中,neff为有效塔板数,n为理论塔板数。
综合公式(6)和(7)可得:

表2 k值对值的影响

表2 k值对值的影响
K0.51.03.05.08.0103050 k/(1+k)0.330.500.750.830.890.910.970.98
由表2可知:
实际分离过程中,改变k'值的有效方法就是改变固定相,使得固定相对复杂的混合样品中不同的待分离组分的作用差距增加,即不同的待分离组分在固定相与流动相之间的分配比差距越大,复杂的混合样品在经过色谱柱时,复杂的混合样品不断地在固定相与流动相之间进行分配并达到平衡,待分离组分在固定相、流动相中反复作用,逐渐累积其在固定相和流动相中的差异,使不同组分逐渐分离,最终达到分离的效果。不同的待分离组分在固定相与流动相之间的分配比差距越大,达到相同分离度所需要的有效塔板数越小,即越容易分离,分离效果越好。
4 小结
在色谱经济分析法中可以借鉴化学领域的色谱分析法,用有效塔板数neff来表达色谱柱的效能,用分离度来表达色谱柱分离混合样本中所达到的分离效果。色谱柱的效能越大,即色谱柱的有效塔板数越大,表示组分在色谱柱中达到分配平衡的次数越多,固定相的作用越显著,色谱柱分离能力发挥的越好,对分离越有利,但是色谱柱的柱效能反映的是色谱峰扩宽的程度,不能反映被分离组分的实际分离效果。被分离组分的实际分离效果取决于待分离的混合物中不同组分在固定相与流动相间分配比的差异大小,分配比的差异大小决定了不同组分经过色谱柱分离后的保留时间的差距,而分离度能够综合考量柱效及分配比和选择性的关系,能准确表示色谱柱的总分离程度。提高分离度的途径有:
(1)提高柱效即增加有效塔板数,增加组分在流动相与固定相间的分配次数是提高分离度的最直接、最简单,也是最有效的手段之一;
(2)增加色谱柱选择性是提高分离度的有效办法之一。首先,选择性r21必须大于1,才能实现混合组分的有效分离,而且r21越大,表明色谱柱的选择性越好,达到相同分离度所需要的有效塔板数越小,越容易分离,分离的效果也越好,分离度越大。实际分离过程中,增加r21值的有效方法就是改变固定相,使得固定相对复杂的混合样品中不同的待分离组分的作用差距增加,即不同的待分离组分在固定相与流动相之间的分配比差距越大,复杂的混合样品在经过色谱柱时,复杂的混合样品不断地在固定相与流动相之间进行分配并达到平衡,待分离组分在固定相、流动相中反复作用,逐渐累积其在固定相和流动相中的差异,使不同组分逐渐分离,最终达到分离的效果。

[1]游士兵,吴比,沈萍,梅敏,苏正华.复杂经济现象分类方法创新的理论前瞻——基于化学“色谱分析法”的借鉴与思考[J].统计与决策,2011,(7).
[2]游士兵,梅敏,吴比.色谱分析法在经济领域中的应用展望[J].统计与决策,2011,(11).
[3]沈萍,张佩,毛锴苑,李跟强,游士兵.色谱经济分析法置换系列研究:分配比[J].统计与决策,2011,(7).
[4]苏立强,郑永杰.色谱分析法(第1版)[M].北京:清华大学出版社.2009.
[5]沈力,田华,鲁昌荣.基于Copula的企业整体风险测度[J].统计与决策,2010(,22).
[6]王浩等.几种常用色谱工作站色谱峰保留时间的确定[J].中国医药工业杂志,2008,39(9).
[7]游士兵,包莉丽,钟双营,管璇,王凌霄.色谱经济分析法置换系列研究:塔板理论[J].统计与决策,2012,(1).
[8]傅若农.色谱分析概论(第2版)[M].北京:化学工业出版社,2005.
[9]Daniel Zeghal,Anis Maaloul.Analysing Value Added as an Indicator of Intellectual Capital and its Consequences on Company Performance[J].Journal of Intellectual Capital,2010,(1)
[10]LI Peng-yan,LUO Qing-sheng,AO Li-feng.The Analysis of Capi⁃tal Structure of Chinese Real Estate Listed Companies[J].Journal of Harbin Institute of Technology,2005,(3).
006-04;F224
A
1002-6487(2013)14-0004-05
沈 萍(1970-),女,湖北武汉人,副教授,研究方向:分析化学。
(责任编辑/亦 民)
