基于交通影响分析的物流园区规模定位研究

徐 超， 孙 焰（同济大学 交通运输工程学院，上海 201804）

XU Chao,SUN Yan (School of Transportation Engineering,Tongji University,Shanghai 201804,China)

0 引 言

近年来，规划建设物流园区已成为我国物流产业发展的重要主题，很多城市掀起了建设物流园区的热潮。然而，一些物流园区项目未经科学论证和统一规划就盲目建设，导致园区建成运营后严重恶化了周边交通环境。另一方面，随着城市化进程日益加快，交通量持续大幅增加，我国城市交通状况日趋严峻，这要求物流园区等城市重大建设项目规划时必须充分考虑对周边交通环境的影响。

规模定位是物流园区规划的重点内容之一，也是决定物流园区对周边交通环境影响程度的重要因素之一。目前国内外已有学者对物流园区规模定位做了相关研究。夏纯欢[1]以分行业的物流量预测为基础，按功能划分物流园区的类型和作业区，探索了作业量同规模的联系，推导出物流园区规模。程世东等[2]分析了货物的种类数、周转量等因素与占地面积的关系，从微观层面给出了确定物流园区规模的经验公式。李玉民等[3]用货运量代替物流量来确定物流园区总规模，从实物量的角度给出物流园区用地总规模的经验公式。Eiich等[4]借助排队论和非线性理论研究物流园区理想区位和规模，设计了双层数学模型。但这些研究均未分析物流园区与周边交通环境的关系，使得规划的物流园区与周边交通系统不匹配，物流园区规模不尽合理，因此存在一定的局限性。

交通影响分析，是指定量分析给定使用性质和规模的土地在开发后对周边交通系统所带来的影响，以评判给定的土地其开发强度是否合适[5]，即判定建设项目的规模是否合理。本文则基于交通影响分析，以周边道路的服务水平不会因物流园区的建设而低于最低服务水平为条件，建立物流园区交通量最优化模型，反推出路网处于用户均衡状态时路网容许的物流园区最大交通生成量，从而得出物流园区能够处理的物流量，再根据公式计算物流园区的规模。

1 物流园区交通量最优化模型的建立与求解

1.1 模型原理

在交通影响分析过程中，需要预测背景交通和建设项目交通。背景交通是指无建设项目时路网上各路段的交通量大小、构成及分布，项目交通是指建设项目产生和吸引的交通量大小及方向。然后以背景交通量为路网 “预荷载”，按四阶段法的思路，将项目交通OD量在路网上进行分配，得到有项目情况下路网的综合交通量，再按照道路服务水平等级评判建设项目对路网的影响程度。

物流园区是货物的集散中心，因此项目交通以货物运输产生的交通为主。根据货物的OD表可得出货运量的空间分布特性，再结合车辆出行比例、满载率各类车辆的运量、转换系数等因子将货运量OD表转换成物流园区与各OD点间的交通分布[6]。与交通影响分析不同的是，该模型将OD量作为能分配到路网上交通量的上限值而非实际值，并按照Wardrop第一原理——用户均衡原理，逐渐为路段分配流量。若某路段上的综合交通量达到上限值——路段最低服务水平时的交通量，则停止交通分配，此时分配到路网的OD量之和即为物流园区的最大交通量。因为经过该路段的某条路径必定是某OD对的最短路径，若再继续分配，则必选择该最短路径，使该路段的交通量超过上限值。若直到所有OD量都分配到路网上时，所有路段交通量都没超过上限值，表明物流园区不会对周边交通环境产生严重影响，则物流园区的最大交通量即为所有OD量之和。

在此模型中，假设物流园区建成运营之前和之后的路网高峰小时重叠。在实际运用中，如果物流园区建成运营之后的路网高峰小时发生变化，则须研究路网交通变化规律，确定新的高峰小时。

1.2 变量说明

假定路网G=（N,A），N为节点集，A为路段集，物流园区记为节点0；为路段 a（ a∈ A）的高峰小时背景交通量，为路段a的项目交通量，Xa为路段a的高峰小时综合交通量；ta为路段a上的广义阻抗费用，ta（0）为路段a上零流时的广义阻抗费用；Ca为路段a的容许交通量，La为路段a在可接受的最低服务水平时交通量占容许交通量的比例；R和S分别为路网中起点和讫点的集合；ψrs为OD对（r,s）间所有路径的集合，r∈R，s∈S；为OD对（r,s）间第k条路径上的高峰小时项目交通分配量；为OD对（r,s）间第k条路径上的广义阻抗费用；为OD对（r,s）间最短路径的广义阻抗费用；为0-1变量，表示如果路段a在OD对（r,s）间第k条路径上，其值为1，否则为0；Qrs为OD对（r,s）间的项目交通量需求。

1.3 模型建立

物流园区交通量的最优化模型可描述如下：

式 （1）为目标函数，表示物流园区的交通产生量、吸引量之和最大化；式 （2）和式 （3）表示各路段的综合交通量不能超过路段交通量上限值；式（4）和式（5）表示OD对r,（）s 间第k条路径上的广义阻抗费用，α和β为常数；式 （6）和式（7）为用户均衡原理的数学表达式；式（8）表示OD对r,（）s间实际的项目交通量应不超过项目交通量需求；式 （9）表示路径流量的非负约束。

1.4 基于改进遗传算法的模型求解

传统遗传算法在应用中存在很多局限性，如过早收敛、接近最优解时收敛较慢。因此，本文对算法做了一些改进，采用改进的遗传算法求解上一节建立的最优化模型，算法具体步骤如下：

1）利用罚函数法将模型转化为无约束的最优化模型：

Z0为必定大于Z的最大值的数，μ为惩罚因子，μ＞0，当μ→∞时，目标函数逼近最优解，自变量

2）确定编码方案：假设路网中共有N个OD对，第n（ n≤）N 个OD对有Kn条路径。采用实数编码，记染色体：

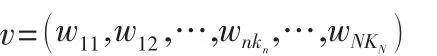
其中，wnkn表示第n个OD对第kn条路径的流量，染色体串的长度为，群体规模为M，设置当前进化代数GEN=0。

3）确定适应度函数：第i条染色体的适应度函数：

5）交叉操作：采用扩大交叉规模的交叉操作[8]，以交叉概率Pc从群体中选出Y条染色体组成交叉库，对交叉库中的每两条染色体均进行一次交叉，将新产生的染色体存入临时种群中，其规模为Y（ Y- 1）。假设交叉库中两条染色体分别为vi和vj，则交叉产生的后代：

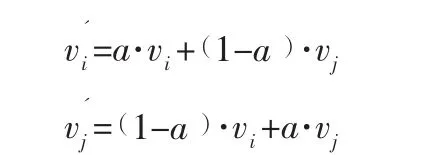
其中，a为［0,1］之间的随机数。将临时种群和交叉库合并，按照适应度值从大到小的顺序依次取前Y条染色体替代父代中交叉操作前的Y条染色体。

6）变异操作：采用自适应变异操作[9]，首先根据适应度值按式 （12）确定每条染色体的变异概率Pm，其中Pm1和Pm2分别为群体最大、最小变异概率，F为染色体的适应度值，Fave为群体的平均适应度值：

再以概率Pm选择参与变异的染色体。为叙述简便，假设染色体v=（w1,w2,…,wB）参与变异，其中，从v中均匀随机地选择一个分量wi，在wi的定义区间中均匀随机地抽取一个数代替wi，从而得到代替v的子代v'。置GEN=GEN+1。

7）确定算法的终止准则：若GEN=Gmax，则算法终止，否则转步骤4）。

2 物流园区规模的确定

物流园区规模定位是物流园区规划的一个重要内容，但由于影响规模定位的因素很多，目前还没有一套成熟的标准和方法。一种普遍采用的方法是，先将货运量转化为物流需求，再利用经验公式计算得出物流园区的规模。因此，先根据车辆出行比例、满载率各类车辆运量、转换系数等因子，将上一节求出的物流园区最大交通量转化为货运量[10]，从而得到物流园区在周边交通环境制约情况下的最大物流量，最后得出物流园区的规模。

在求得物流园区与各小区间的允许项目交通量后，根据各类车辆出行比例、转换系数，可计算出物流园区与各小区间各类车辆的出行数。

其中，Xrs为OD对（r,s）间各类车辆的出行总数，Vrs为OD对（r,s）间的允许项目交通量，为OD对 （r,s）间各类车辆的出行比例向量，E为车辆转换系数向量。

根据各类车辆出行数、出行比例、净载重量利用率、额定载重量，可以计算出物流园区与各小区间的货运量。

其中：Qrs为OD对（r,s）间的货运量；Brs为OD对（r,s）间各类车辆的静载重利用率矩阵；C为各类车辆的额定载重量向量。物流园区的每日处理的货运总量：

其中，P为高峰时货运量占全天货运量的比例。物流园区规模的计算公式：

其中：S为物流园区规模 （单位：公顷）；γ为物流园区周转系数，由物流园区的类型决定；ε为物流园区单位生产能力用地参数 （单位：公顷/万吨），表示每日处理一吨货物需要物流园区的面积；λ为物流园区作业场面积占总面积的比重。

3 案例分析

图1是某市规划的一个物流园区的区位图，该园区将于2015年建成，其货物流向主要有6个，为图中标记的第1～6个小区。经预测，目标年各方向的高峰小时货运量需求如表1所示，目标年各条路段的高峰小时背景交通量和负荷度如图1所示。

表1 物流园区 （0）与各方向高峰小时货运量需求分布 （t）

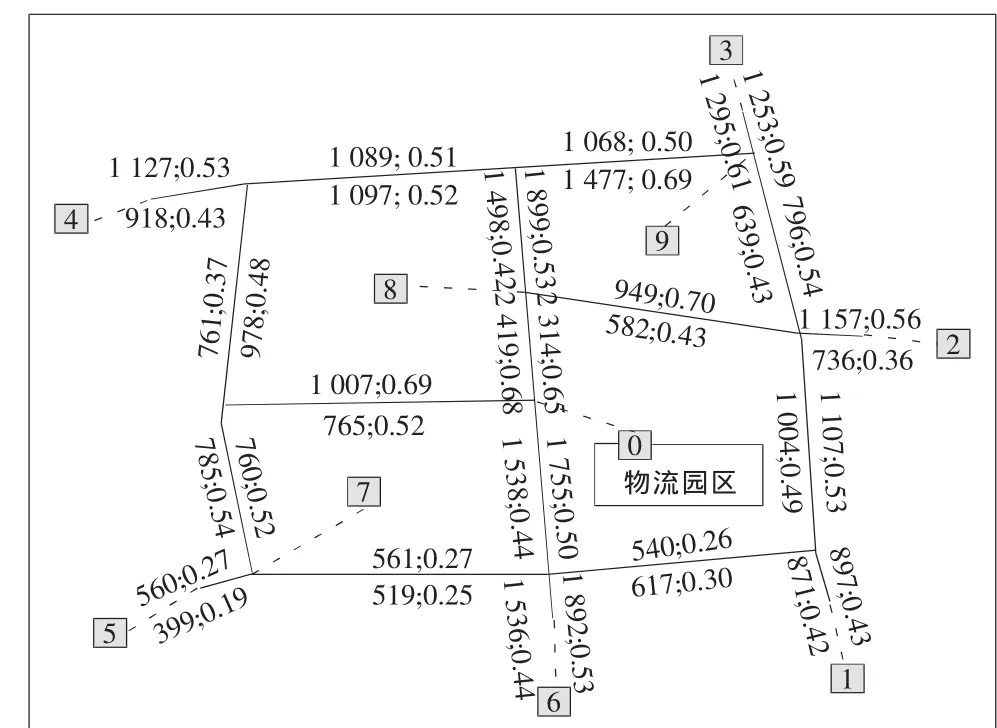
图1 物流园区区位、目标年路段背景交通量及负荷度

图2 目标年各路段综合交通量及负荷度

通过建立模型并计算得出目标年各条路段的高峰小时综合交通量和负荷度，如图2所示。从图2可以看出，有3条路段的负荷度已经达到了0.75（用黑色五角星标记），为路段允许的最大负荷度。此时，实际的高峰小时项目交通量已经达到最大值。由式 （13）和 （14）求得物流园区与各方向之间的实际货运量，如表2所示。

表2 物流园区 （0）与各方向高峰小时实际货运量分布 （t）

由式 （15）和 （16）求得物流园区每日处理的货运量为Q=3042（）t，物流园区规模为S=215.28（ha）。

4 结束语

物流园区不是一个孤立的系统，其发展必须与所处的交通系统相适应。因此，确定合理的物流园区规模时必须考虑周边道路流量变化情况。本文在利用传统的经验公式计算物流园区规模的方法基础上，以交通分配的用户均衡为原则，建立了物流园区交通量的最优化模型，并结合交通影响分析，保证了路段流量在上限值范围内。改进的遗传算法克服了传统算法的一些不足，提高了运算效率和准确度。算例表明本文的思路和方法对物流园区受周边交通环境制约时的规模定位研究是可行、有效的。

[1]夏纯欢.城市物流园区合理规模与布局选址研究[D].成都：西南交通大学 （硕士论文），2008：16-33.

[2]程世东，刘小明.时空消耗法求解物流园区规模[J].公路交通科技，2005(8)：142-144.

[3]李玉民，李旭宏，毛海军,等.物流园区规划建设规模确定方法[J].交通运输工程学报，2004,4(2)：76-79.

[4]Eiichi Taniguchi,Michihiko Noritake,Tadashi Yamada,et al.Optimal size and location planning of public logistics terminals[J].Transportation Research Part E,1999,35(3)：207-222.

[5]建设项目交通影响评价课题组.建设项目交通影响评价[M].北京：中国建筑工业出版社，2007.

[6]彭驰.物流园区交通影响分析研究[D].长沙：长沙理工大学 （硕士论文），2007：17-20.

[7]杨平，郑金华.遗传选择算子的比较与研究[J].计算机工程与应用，2007,43(15)：59-62.

[8]冯冬青，王非，马雁.一种扩大交叉规模的自适应遗传算法[J].计算机工程与应用，2008,44(9)：73-75.

[9]叶甲秋，楼佩煌.改进的自适应遗传算法及其在系统参数辨识中的应用[J].电工电气，2010(3)：29-32.

[10]马玉红.物流园区交通影响分析方法研究[D].长春：吉林大学 （硕士论文），2008：18-20.