基于自适应参数估计的反推终端滑模再入飞行控制

史 震，张玉芳，孙 蓉，马文桥，林 强

(1.哈尔滨工程大学 自动化学院，150001哈尔滨;2.空军航空大学，130022长春)

空天飞行器(aerospace vehicle，ASV)再入飞行段，大攻角的高速再入造成了飞行器速度、高度和姿态的极大变化，其运动方程表现出强非线性及耦合等动态特性.其次，ASV的再入飞行存在大量的外界干扰，以及ASV内部参数的不确定性等问题［1］.因此，传统的控制方法已经无法满足飞行控制系统的设计要求，必须寻求更为有效的方法进行ASV控制系统的设计.

近年来，自适应反推控制已成功应用到飞行控制设计中［2-6］.文献［3-5］分别对存在不确定性的飞行器系统设计了自适应控制器，这种方法通常要求系统的不确定性的界已知或满足线性增长条件，而飞行环境恶劣的ASV系统显然很难满足要求.因此，从飞行器内部参数的不确定性考虑，文献［7-8］将未知气动参数看作待估计参数矩阵或向量，采用自适应策略补偿气动参数不确定性引起的控制系统性能的下降，降低了控制器设计对于系统模型的要求.

本文建立了ASV的具有时变参数的严格反馈形式的被控模型，将ASV未知气动参数转化为待估计参数矩阵或向量，设计自适应律在线估计飞行器控制模型的气动参数.与文献［2-6］相比，充分利用了系统的已有信息，并结合自适应反推控制、滑模控制，提出了一种基于自适应反推法的终端滑模控制方法，并通过Lyapunov稳定性理论证明了闭环系统所有误差一致最终有界.该方法放宽了系统模型参数不确定的限制，对于系统内部参数变化具有很强的鲁棒性.

1 模型的建立

1.1ASV的动力学模型

ASV姿控模型是一类不确定仿射非线性系统［9］.根据时标分离原理，可分为快慢不同的4组［10］，控制系统设计按照其中两组变量进行设计，较慢变量α，β，γ分别为攻角、侧滑角与滚转角;快变量p，q，r分别为滚转角速度、俯仰角速度与偏航角速度.其非线性动态方程描述为

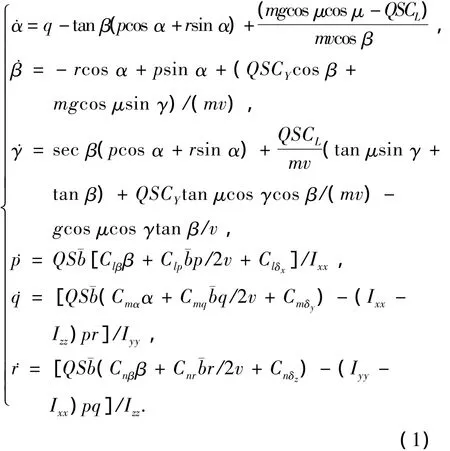
式中:δx，δy，δz分别为副翼偏转角、升降舵偏角和方向舵偏角;μ为弹道倾角;m为质量;v为飞行速度为平均气动弦长;Q为动压;S为参考面积;CL，CY，Clβ，Clp，Cmα，Cmq，Cnβ，Cnr均为气动参数;Ⅰxx，Ⅰyy，Ⅰzz为不同方向上的转动惯量.

1.2ASV不确定模型的建立

ASV利用地球的稠密大气在再入过程中减速下降，这使得其飞行环境和气动特性具有快速时变的特性.因此，ASV的控制问题是一个快速时变参数的非线性系统稳定性问题.通过分析其动态模型，将未知气动参数转换为待估计参数向量θ1、θ2或矩阵θg，则被控模型转化为

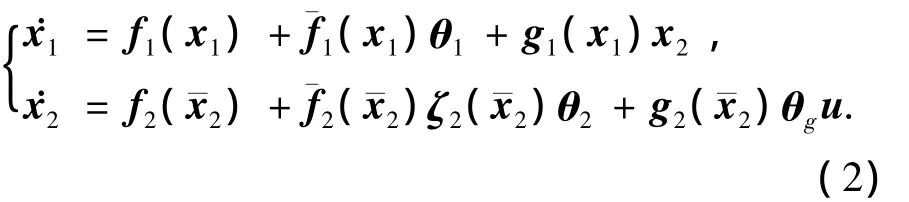
将f1(x1)简单记为f1，其余矩阵函数作类似处理，则式(2)可改写为

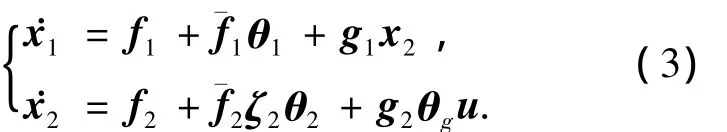
式中:

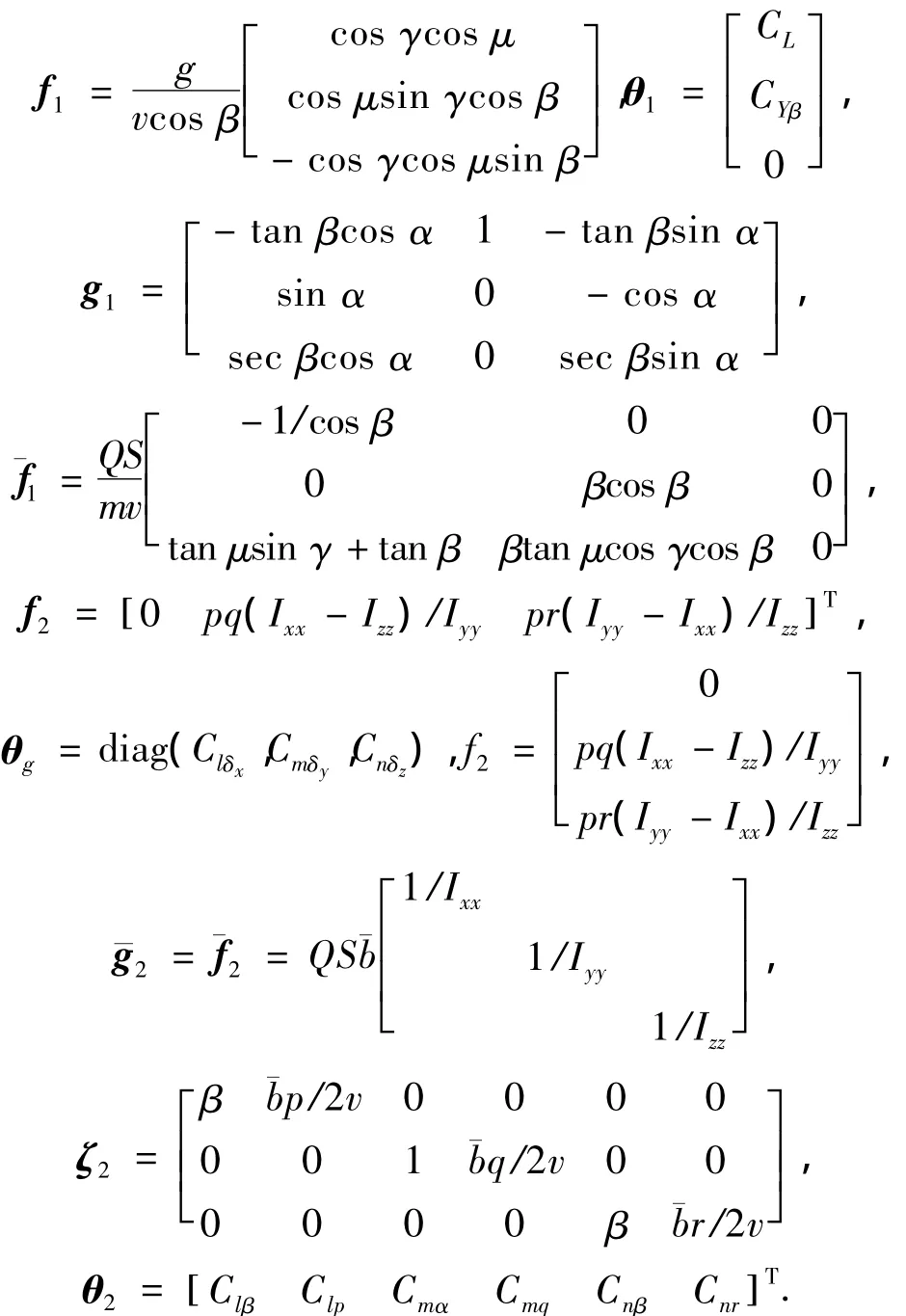
2 自适应动态面控制

ASV控制器设计的目标是针对式(3)，通过设计控制器消除不确定性的影响，使系统的输出y(t)跟踪期望的参考轨迹yd(t).为了设计反推终端滑模控制器，需要如下假设条件:1)给定的参考信号yd(t)连续可导且n阶导数有界.2)在紧集Ω上，｜g1｜≠0，且存在常数σ10、σ11，使得0＜σ10≤‖g1‖≤σ11;｜g2θg(t)｜≠0，且矩阵的最小奇异值σ，满足对∀ε＞0，σ≥ε，∀x∈Ω.

针对式(3)，采用反推法进行控制器设计，控制结构如图1所示，具体设计步骤如下.

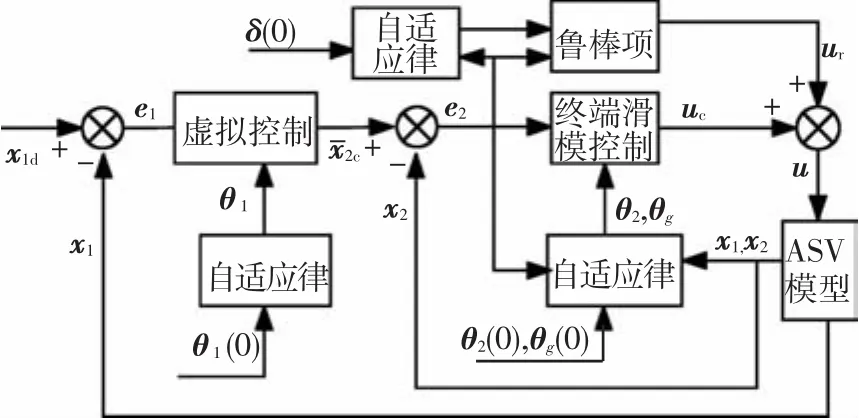
图1 基于自适应参数估计的反推终端滑模控制系统图

步骤1针对x1子系统，以x2为虚拟控制输入，使得角度x1=［α，β，γ］T的跟踪误差一致最终有界，定义跟踪误差变量e1=x1-x1d，则

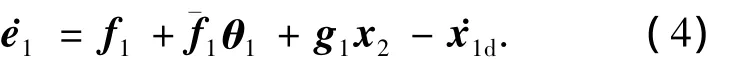
选择虚拟控制输入x2c为

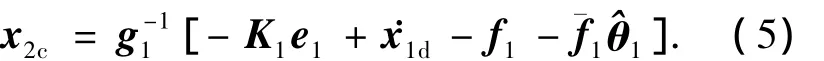
其中:K1为正定的对角矩阵，1为参数θ1的估计值.

需要注意的是，在实际控制量u的设计过程中，为了避免对x2c进行求导.引入一阶低通滤波器［11］对虚拟控制律进行滤波，以降低计算的复杂性.滤波器动态方程为

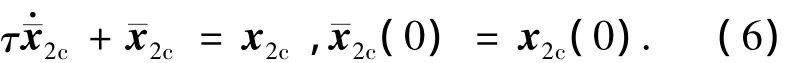
式中:τ为设计的滤波时间常数，τ＞0.

为保证闭环系统的稳定性，定义虚拟控制量的滤波误差为

将式(5)、(7)代入式(4)得

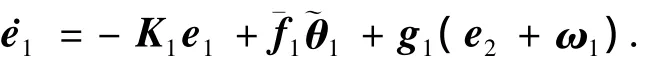
定义Lyapunov函数为

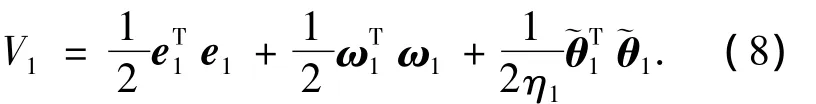
根据假设条件，可知

将式(11)、(12)代入式(10)，得

步骤2对于x1，x2组成的系统，设计控制输入u，使得x1-x1d，x2-x2c一致最终有界.基于终端滑模具有有限时间收敛的优点，在控制器设计中引入滑模控制，设计滑模面

式中:e2=x2-x2c，a＞0，b＞0，q＜p，且q，p均为正奇数.

取控制量uc与参数θ2，θg的自适应律分别为

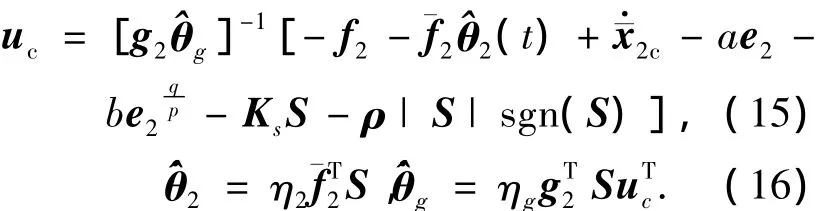
式中:Ks，ρ为正定对角矩阵;η2，ηg＞0,分别为参数θ2，θg估计值，由于g2是通过在线估计θg得到的，很难保证其非奇异性，因而采用广义逆

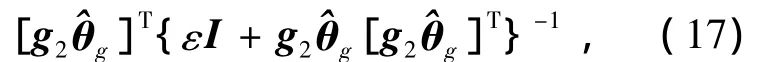
代替g2的逆.

如果式(15)采用g2的广义逆矩阵，为了保证闭环系统稳定性，在式(3)的控制器设计中引入鲁棒项［12］ur，则设计控制量

其中:

定理考虑式(3)，在假设条件1)、2)成立的条件下，根据上述设计过程，通过恰当的选择正定对角矩阵K1，Ks，ρ，正常数τ，a，b，p，q，ρ，δ(0)，基于Lyapunov稳定性理论，采用虚拟控制量式(5)与实际控制量式(18)～(22);参数调节律采用式(9)、(16)，则闭环系统所有信号一致最终有界．

证明 为证明闭环系统所有误差信号一致最终有界，定义Lyapunov函数V2=V1+Vs，

由式(13)可知，若设计合理的控制量u，使得e2收敛到零，则可保证x1的跟踪误差e1与滤波误差ω1一致最终有界.

下面证明采用控制量式(18)～(22)，使得系统的跟踪误差e2收敛到零.

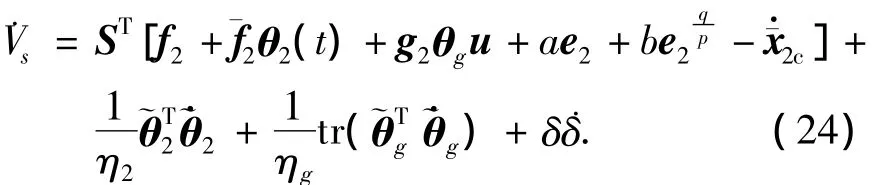
将式(16)、(18)～(22)代入式(24)，得

根据假设条件2)，有

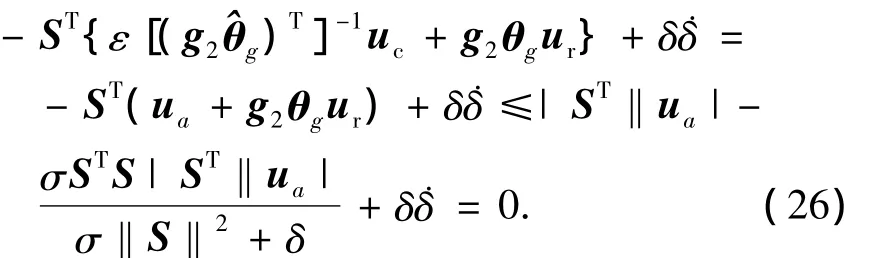
则

当S≠0时，＜0，跟踪误差e2在有限时间内收敛到零.且由文献［13］的引理4.3可知，在紧集Ω上，存在一个实数C＞0，使得‖2c‖2＜C.则式(13)可转化为

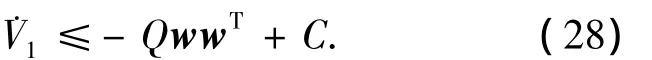
3 仿真验证

为验证本文所设计控制方法的正确性和有效性，针对ASV再入姿态控制进行了仿真和分析.设定ASV模型的初始条件:m=641 kg，H=30 km，b=0.8 m，S=0.502 4 m2，v=2 500 m/s，v声=301.805 m/s，ρ=0.018 4 kg/m3，g=9.757 m/s2，μ0=-21.6°，α0=0°，β0=0°，γ0=0°.取δ(0)=1，自适应律系数设计为η1=3，η2=5，ηg=0.5.

分两种情况进行对比仿真.当飞行器气动参数无摄动时，将确定ASV系统的常规反推控制效果，与系统含有自适应估计参数时的反推控制效果相比较，仿真结果如图2、3所示，为简便起见，常规反推控制器参数选取为K1=diag(10，5，10)，K2=diag(25，25，15).

图2 气动参数无摄动时的角度响应曲线

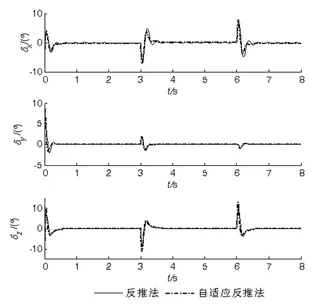
图3 气动参数无摄动时的舵偏角

图2、3分别给出了角度跟踪曲线与舵偏角曲线.由图可见，在系统参数无摄动时，将气动参数看作待估计的参数向量或矩阵，所设计的带有自适应参数估计的反推控制器具有良好的控制效果.仿真过程中未出现发散现象，由此也说明，通过引入矩阵的广义逆，避免了控制增益参数估计过程中可能出现的奇异现象.

当气动参数存在摄动情况下，设计自适应反推终端滑模控制器.选取参数为a=1，b=0.1，q=5，p=7，K1=diag(10，8，10)，Ks=diag(20，20，15)，ρ=diag(20，20，15).将常规反推控制效果与自适应反推终端滑模控制效果进行比较，仿真结果如图4、5所示.

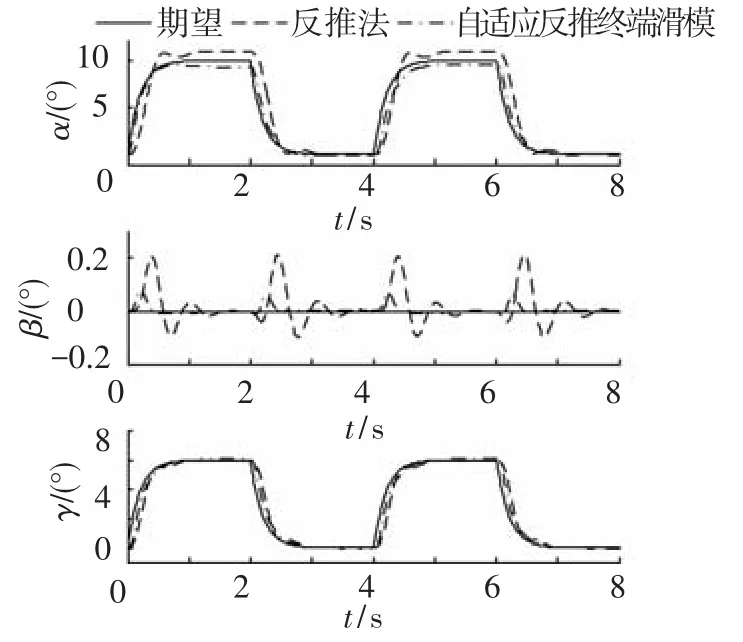
图4 气动参数摄动-50%时的角度响应曲线

图5 气动参数摄动-50%时的舵偏角

由图4、5可知，在不考虑初始段偏差的情况下，采用常规反推控制器得到的攻角、侧滑角和滚转角最大跟踪误差分别为0.926°，0.141°，0.024 8°;而含有自适应估计参数时的反推终端滑模控制器得到的攻角、侧滑角和滚转角最大跟踪误差分别为0.046 5°，0.089°，0.023 8°.通过比较可以看出，当系统参数存在摄动时，含有自适应估计参数的反推控制中引入滑模面，一方面使超调量有所减小，实现了对不确定参数的稳定估计，增强系统对于参数大幅度摄动的适应能力，另一方面可有效提高控制收敛速度与控制精度.

4 结论

1)针对ASV再入飞行时，外界环境剧烈变化造成的系统参数不确定性问题，建立了具有时变参数的严格反馈形式的ASV被控模型，提出了基于自适应参数估计的反推终端滑模控制设计方法.

2)通过理论推导与仿真实验表明，该方法使得闭环系统所有信号一致最终有界并且跟踪误差收敛到给定轨迹的任意小范围内.与传统反推控制器相比，减小了误差系统的收敛时间和系统的稳态跟踪误差.对于参数不确定的ASV系统，该方法具有较强的鲁棒性.

［1］方炜.空天飞行器再入飞行模糊自适应预测控制［D］.南京:南京航空航天大学，2008.

［2］范金锁，张合新，张明宽，等.基于自适应二阶终端滑模的飞行器再入姿态控制［J］.控制与决策，2012，27(3):403-407.

［3］张强，吴庆宪，姜长生，等.近空间飞行器鲁棒自适应Backstepping控制［J］.系统工程与电子技术，2012，34(4):754-761.

［4］黄喜元，王青，董朝阳.基于Backstepping的高超声速飞行器鲁棒自适应控制［J］.系统工程与电子技术，2011，33(6):1321-1327.

［5］高道祥，孙增圻，罗熊，等.基于Backstepping的高超声速飞行器模糊自适应控制［J］.控制理论与应用，2008，25(5):805-810.

［6］李海军，黄显林，葛东明.再入机动飞行器自适应轨迹线性化控制［J］.宇航学报，2011，32(5):1039-1046.

［7］曹立佳，张胜修，刘毅男，等.带有自适应参数近似的块控反步飞行控制器设计［J］.航空学报，2011，32(12):2259-2267.

［8］袁国平，史小平.带有特殊不确定性的导弹非线性自适应控制［J］.电机与控制学报，2010，14(5):104-108.

［9］SNELL S A.Nonlinear dynamic-inversion flight control of supermaneuverable aircraft［D］.Kansas:University of Kansas，1991:24-27.

［10］李海军，黄显林，葛东明.再入机动飞行器自适应轨迹线性化控制［J］.宇航学报，2011，32(5):1039-1046.

［11］曾宪法，王小虎，张晶，等.高超声速飞行器的干扰补偿Terminnal滑模控制［J］.北京航空航天大学学报，2012，38(11):1444-1448.

［12］LABIOD S，BOUCHERIT M S，GUERRA T M.Adaptive fuzzy control of a class of MIMO nonlinear systems［J］.FuzzySetsandSystems，2005，151:59-77.

［13］HASSAN K K.Nonlinear systems［M］.3rd ed.Beijing:PublishingHouseofElectronicsIndustry，2007:145.