双主跨悬索桥颤振节段模型试验模态匹配问题

张文明，葛耀君

(1.东南大学混凝土及预应力混凝土结构教育部重点实验室，210096南京;2.同济大学土木工程防灾国家重点实验室，200092上海)

多主跨悬索桥作为一种新兴桥型已崭露头角，中国已揭开建设大跨度多主跨悬索桥的序幕，多主跨悬索桥凭借良好的经济性和巨大的跨越能力在跨海连岛工程中有着广阔应用前景［1］.

与传统单主跨悬索桥相比，多主跨悬索桥由于中间桥塔缺乏有效的纵向约束，结构刚度降低，对风作用的敏感性增强，风致振动问题是控制其设计的重要因素之一.其中，颤振稳定性是关系到多主跨悬索桥安全性的重要课题.近年来，中国学者以泰州大桥和马鞍山大桥为契机，日本学者以丰予(Ho-yo)海峡多主跨悬索桥为契机对多主跨悬索桥颤振稳定性进行了研究［4-10］.

早期研究主要针对多主跨悬索桥结构布置，尤其是中间塔刚度对颤振临界风速的影响，而且计算多采用近似简化公式.1998年，文献［4］从三塔四跨悬索桥参数分析中发现，随着中塔的刚度增大，颤振的临界风速几乎不变，甚至还有所降低.文献［5］认为三塔四跨悬索桥的颤振振型是一阶反对称竖弯和一阶反对称扭转的组合，并利用Selberg公式计算了颤振临界风速.2001年，文献［6］利用Selberg公式对一个三塔四跨悬索桥的颤振临界风速进行计算，分析了中塔抗扭刚度对颤振临界风速的影响.2008年，文献［7］对泰州大桥设计中选取了1/7～1/13范围内的垂跨比进行动力方面比较，随主缆垂跨比加大，双主跨悬索桥颤振临界风速微幅提高.

2009年，文献［2，8］报道了在马鞍山大桥全桥气弹模型风洞试验中发现的颤振形态演化现象.2011年，文献［9］通过节段模型风洞试验研究了检修车轨道的位置对泰州大桥颤振临界风速的影响.文献［10］提出了考虑静风作用的全模态颤振算法，讨论了静风作用对多主跨悬索桥颤振的影响，在颤振临界风速和颤振形态等方面与传统的单主跨悬索桥进行了对比分析.

与传统单主跨悬索桥相比，中间塔的引入使得多主跨悬索桥的颤振发散出现了多种可能的弯扭模态组合.弹簧悬挂节段模型风洞试验是确定桥梁颤振临界风速的一种经济有效的常用方法.在多主跨悬索桥的节段模型风洞试验中，如何匹配竖弯模态与扭转模态?哪种弯扭模态组合的颤振临界风速最低?鲜有文献报道相关研究.

本文以马鞍山大桥为工程背景，根据模态相似性匹配出3种弯扭模态组合，在节段模型试验中测试了各组合的颤振临界风速，并对结果进行比较分析.

1 工程背景

马鞍山大桥是一座跨径布置为360 m+2×1 080 m+360 m的三塔双主跨悬索桥，见图1.加劲梁为扁平钢箱梁，无中央开槽，宽38.5 m，高3.5 m，见图2.该桥详细介绍见文献［2］.

图1 马鞍山大桥总体布置(m)

图2 马鞍山大桥钢箱梁标准断面(mm)

2 模态匹配

采用有限元方法计算获得该桥的主要6阶模态见图3［2］.加劲梁节段模型测振试验模拟结构竖向和扭转方向两个自由度的振动特性，水平来流方向即阻力方向的振动特性一般不模拟.对于传统的单主跨悬索桥，一般认为颤振形态是第一阶竖弯模态和第一阶扭转模态的组合，在测振风洞试验中选取竖弯基频和扭转基频来计算节段模型的频率.而双主跨悬索桥存在颤振弯扭模态匹配问题，严格来讲在节段模型试验中是弯扭模态之间频率和等效质量匹配问题，一阶对称和反对称竖弯模态与一阶扭转和反对称扭转模态有4种组合，但是其中一阶对称竖弯模态(S-V-1)和一阶反对称扭转模态(A-T-1)无论是在全桥还是在单跨完全没有相似性［2］，它们的组合可不予考虑，因此本文进行了表1所示3种组合的颤振试验.

图3 马鞍山大桥一阶模态

表1 竖弯与扭转模态匹配

3 模型设计与制作

节段模型采用几何缩尺比λL=1∶70，质量缩尺比λm=1∶702，质量惯性矩缩尺比λⅠm=1∶704，频率缩尺比λf=17.5∶1，风速缩尺比λv=1∶4，阻尼缩尺比λξ=1.根据测振节段模型设计相似性要求，可确定测振节段模型相似比.由此进一步确定实桥结构主要参数与节段模型主要参数的对应关系，见表2.节段测振模型为薄壁箱形结构，由铝合金框架与杉木板覆面组成，桥面栏杆、检修轨道和风嘴等均选用ABS材料雕刻而成，节段模型断面见图4.

表2 实桥与节段模型主要参数的对应关系

图4 马鞍山大桥节段模型断面(mm)

4 结果及分析

节段模型测振试验在同济大学土木工程防灾国家重点实验室TJ-1边界层风洞中进行.加劲梁节段模型采用洞外支架悬挂，整个节段模型测振悬挂系统见图5.

图5 节段模型测振悬挂系统

根据表1中每种模态组合，在均匀风场中分别进行了-5°、-3°、0°、3°和5°五个攻角下的颤振临界风速测试，不同风攻角下的颤振临界风速换算到实桥见表3.可看出:1)各组合的颤振临界风速最小值均大于检验风速，因此马鞍山大桥具有很好的颤振稳定性;2)相同攻角下模态A-V-1与A-T-1组合(组合1)的颤振临界风速最低，因此模态A-V-1与A-T-1是双主跨悬索桥二维颤振的控制组合;3)相同攻角下模态S-V-1与S-T-1组合(组合2)的颤振临界风速略低高于模态A-V-1与S-T-1组合(组合3).

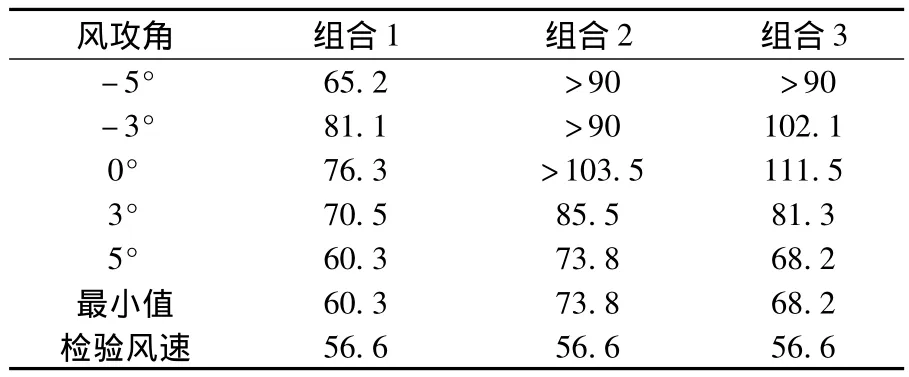
表3 不同攻角下的颤振临界风速m·s-1

上述结论可用古典耦合颤振的Van der Put公式和Selberg公式［11］来分析解释.

1)Van der Put公式.根据Theoderson平板气动力的精确表达式，由Klöeppel和Thiele算出无量纲参数的诺模图(其中偏保守地忽略了结构阻尼比).Van der Put将诺模图中的曲线拟合成近似的直线式，表示为

式中:ε为扭弯频率比，ε=ωt/ωb=ft/fb;μ为桥面质量与空气的密度比，μ=m/(πρb2);r为桥梁的惯性半径(m )为桥面宽度之半(m)，b=B/2.

2)Selberg公式.根据Theoderson平板气动力公式，由Bleish的颤振解得的近似公式为

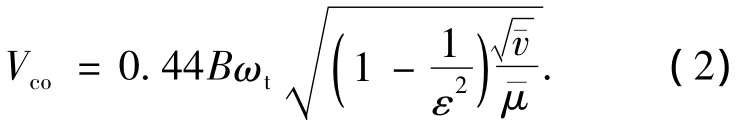
利用上述两个公式估算马鞍山大桥不同模态组合在0°攻角下的颤振临界风速，见表4、5.

表4 Van der Put公式估算不同组合的颤振临界风速

表5 Selberg公式估算不同组合的颤振临界风速

Selberg公式计算结果高于Van der Put公式计算结果，因为前者考虑了阻尼的有利影响，后者没有.综合分析表4、5可发现:1)组合1的颤振临界风速最低，这与表3节段模型试验结果一致.主要是由扭转圆频率差别造成的，该参数对计算结果起决定性作用;2)组合2的颤振临界风速略小于组合3，主要是扭弯频率比的差别造成的.与表3节段模型试验结果不一致，可能是由于节段模型试验中组合2和组合3的阻尼比不同造成的，它们的实测扭转阻尼比分别是0.63%和0.45%.

5 结论

1)相同攻角下，一阶反对称竖弯与一阶反对称扭转模态组合的颤振临界风速最低，因此该组合是双主跨悬索桥二维颤振的控制组合.

2)相同攻角下，一阶对称竖弯与一阶对称扭转模态组合的颤振临界风速略高于一阶反对称竖弯与一阶对称扭转模态组合的颤振临界风速.

3)古典耦合颤振的 Van der Put公式和Selberg公式能预测各组合的颤振临界风速相对大小关系，但不能准确预测颤振临界风速数值.

［1］项海帆.21世纪世界桥梁工程的展望［J］.土木工程学报，2000，33(3):1-6.

［2］张文明，葛耀君，周志勇，等.双主跨悬索桥颤振稳定性试验研究［J］.中国公路学报，2010，23(4):58-62.

［3］张文明.多主跨悬索桥抗风性能及风致灾变全过程研究［D］.上海:同济大学，2011.

［4］LARSEN A.Bridge aerodynamics［M］.Balkema:Rotterdam，1998.

［5］严国敏.6 000 m海峡通道采用的两个悬索桥方案［J］. 国外公路，1998，18(1):26-30.

［6］ YOSHIDA O，OKUDA M，MORIYA T.Structural characteristics and applicability of four-span suspension bridge［J］.Journal of Bridge Engineering，ASCE，2004，9(5):453-463.

［7］杨进，徐恭义，韩大章，等.泰州长江公路大桥三塔两跨悬索桥总体设计与结构选型［J］.桥梁建设，2008(1):37-40.

［8］GE Y J，XU L S，ZHANG W M，et al.Dynamic and aerodynamic characteristics of new suspension bridges with double main spans［C］//Seventh Asia-Pacific Conference on Wind Engineering.Taipei，Taiwan:International Associations for Wind Engineering，2009.

［9］王达磊，马如进，陈艾荣.泰州长江公路大桥三塔悬索桥的颤振稳定性［J］.桥梁建设，2011(1):26-29.

［10］ZHANG W M，GE Y J，LEVITAN M L.Aerodynamic flutter analysis of a new suspension bridge with double main spans［J］.Wind and Structures，2011，14(3):187-208.

［11］李国豪.桥梁结构稳定与振动(修订版)［M］.北京:中国铁道出版社，2002.

［12］JTG/T D60—01—2004公路桥梁抗风设计规范［S］.北京:中华人民共和国交通部，2004.