基于UIO的减摇鳍控制系统故障诊断算法

孙 蓉，刘 胜，李 冰

(哈尔滨工程大学自动化学院，150001哈尔滨)

为达到船舶安全航行以及稳定船舶航行姿态，目前广泛采用减摇鳍装置，这种主动减摇装置集合了电子、机械以及液压技术，通过测量船舶摇摆姿态信息，经控制器处理，输出鳍角控制指令，经液压驱动系统使鳍转动，随着变化的船舶横摇运动而不断地改变鳍运转方向，产生抵抗海浪干扰的稳定力矩，从而达到稳定船舶的横摇姿态的目的.

减摇鳍设备物理结构复杂，涉及技术较多，国内外进行了广泛研究［1-5］.其减摇效果与采用的控制策略密切相关，目前广泛采用变参数最优控制［6-7］、自适应控制［8-9］、模糊控制［10-11］、滑模变结构控制［12-14］等.由于减摇鳍工况环境以及自身设备仪器老化等原因，使减摇鳍控制系统产生故障，导致系统控制减摇鳍失效，危及船舶的安全航行．近几年来，我国的船舶行业高速发展，对减摇鳍的减摇性能以及可靠性方面要求显著提高．由于减摇鳍系统的先进性和结构的复杂性也使系统故障率大大提高，而且故障修复的时间也越来越长，这大大提高了减摇鳍控制系统故障的维修难度．本文以NJ5型减摇鳍控制系统为研究对象，采用基于模型的故障诊断方法，提出了一种UIO最优故障诊断算法，给出算法实现流程，算法采用离散迭代形式便于计算机实现，推导了NJ5型减摇鳍控制系统存在UIO最优故障诊断观测器的充要条件，算法结构紧凑可靠适合工程实现．

1 问题描述

减摇鳍控制系统是一个典型的电液控制系统，为达到减摇鳍可靠运行的目的，本文设计了减摇鳍控制系统实时故障诊断算法，采用哈尔滨工程大学研制的NJ5型减摇鳍为原型，其中NJ5型减摇鳍控制系统原理图如图1所示．

图1 NJ5型减摇鳍控制系统原理图

基于模型的减摇鳍控制系统故障诊断中，评价残差信息判断故障是否发生，对于随动系统状态空间描述为

其中:x系统状态，x=［a，a］T，a为鳍角，a为鳍角速度;y为鳍角输出;u为随动系统的鳍角指令，即为NJ5型减摇鳍航速灵敏度调节器的输出电压．

NJ5型减摇鳍的系统参数为

减摇鳍控制系统实质上是一个海浪随机扰动下的船舶控制系统，集合了电子、电气及液压技术的复杂控制系统，统计了NJ5型减摇鳍使用情况，总结了该型减摇鳍的易发故障部位，本文结合NJ5型减摇鳍实际情况，考虑了控制系统的传感器故障，为了便于系统实际应用实现，将式(1)进行离散化处理，则带有传感器故障以及模型不确定性Edk的随动系统离散化模型为

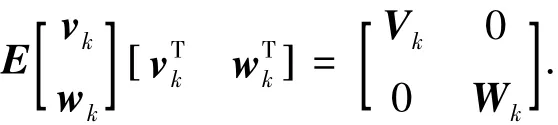
二元假设HEA0、FAU1分别为无故障状态及故障状态，本文目的为设计合适的残差信号rk，Γ(rk)为待设计的残差信号rk的函数.满足逻辑关系为

2 减摇鳍控制系统的UIO观测器设计

本节针对减摇鳍控制系统进行了最优滤波与鲁棒故障诊断的研究，本节设计的全阶UIO(未知输入观测器)，结构简单，相比其他降阶方法，其存在性更容易证明，在满足干扰解耦的条件下还有更多的设计余度．本节给出了UIO的设计步骤并证明了其存在条件，利用干扰解耦原理，获得了最优输出估计．

为了估计式(2)描述的具有未知干扰及故障的减摇鳍控制系统状态，提出了基于待设计参数为Fk+1、Tk+1、Hk+1、Kk+1的UIO最优故障诊断观测器为

这种UIO最优故障诊断观测器的结构框图如图2所示，将UIO最优故障诊断观测器应用到减摇鳍控制系统，考虑带有传感器故障以及模型不确定性Edk的减摇鳍控制随动系统式(2)以及UIO最优观测器式(3)，可得到系统状态估计误差为

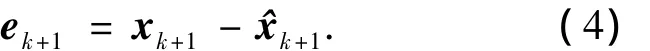
图2 UIO最优故障诊断观测器结构框图

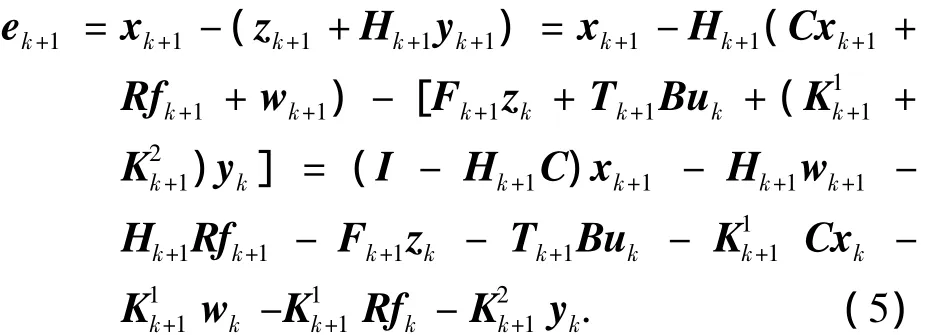
由UIO最优观测器式(3)可知:zk=k-Hkyk，代入状态估计k，因此有

将式(6)代入状态估计误差ek+1，有

代入减摇鳍随动控制系统离散化模型式(2)，有

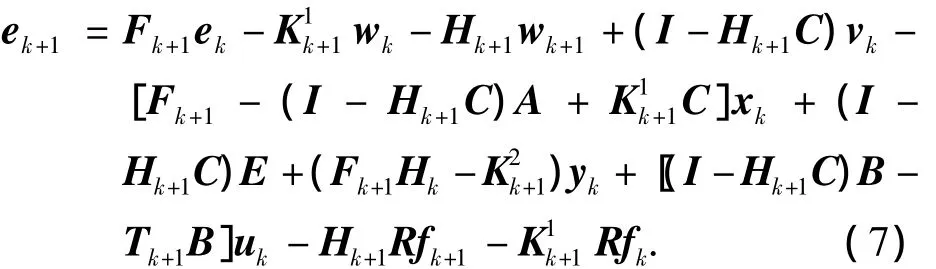
本文设计的UIO最优故障诊断观测器的目的是在减摇鳍控制系统的故障诊断过程中，减小误报、漏报率，提高故障诊断的鲁棒性，为达到设计目的，状态估计误差式(7)利用干扰解耦原理，因此设计的减摇鳍控制系统UIO最优故障诊断观测器参数满足方程

所以得到的干扰解耦的状态估计误差为

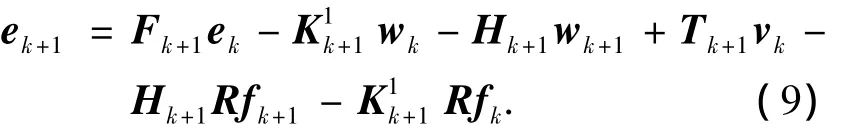
由式(9)可知，若Fk+1具有全部稳定的特征值，在无故障的情况下，状态估计误差ek+1渐进趋于零，即所设计的减摇鳍控制系统UIO最优故障诊断观测器就是求解式(8)，并且Fk+1的特征值稳定.因此具有结构(3)的观测器为减摇鳍控制系统(2)的UIO最优故障诊断观测器的充要条件时，减摇鳍控制系统的状态矩阵满足如下定理．

定理1结构(3)为系统(2)的UIO最优故障诊断观测器的充要条件为:1)rankCE=rankE;2)(C，A1)可观测，其中A1=A-E［(CE)TCE］-1(CE)TCA.

证明充分性．当条件1)成立时，不失一般性，E假定为列满秩矩阵，因此矩阵CE为一列满秩矩阵，所以CE存在左逆阵(CE)+=［(CE)TCE］-1(CE)T，则由E=Hk+1CE，得Hk+1的特解为

则UIO最优故障诊断观测器的系统动态阵为

由式(11)可知，通过合理地设计故障诊断观测器参数K1

k+1可使系统阵Fk+1稳定，满足UIO故障诊断观测器可干扰解耦的参数由式(8)可解．因此设计的结构(3)故障诊断观测器为减摇鳍控制系统的UIO最优故障诊断观测器．

证明必要性．因为结构(3)为系统(2)的UIO最优故障诊断观测器，且未知扰动分布阵E为列满秩矩阵，因此矩阵Hk+1的通解可求，即

其中:H0k+1为任意阵，(CE)+为CE的左逆，即

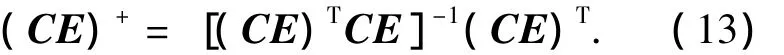
将式(12)代入UIO最优故障诊断观测器的系统动态阵Fk+1，得

由于系统状态阵Fk+1稳定，则矩阵对(，A1)可观测，因此矩阵对(C，A1)可观测.

针对数学易错题、典型习题，通过微课程的整合，分门别类整理，或者讲解易错的地方，强调错误点，方便学生进行纠错，或者从问题引导学生思考，为学生创造一个最近发展区，构建一类问题解决的策略.对于自己解决不了的问题，可以通过先看具体的解答步骤，或多次重复观看，依据微视频的帮助，掌握解题技能，形成策略性知识，发展数学思维，培养学习兴趣.

结构(3)为减摇鳍控制系统(2)的UIO最优故障诊断观测器的充要条件1)说明了可解耦的最大干扰的个数不能大于独立测量的数目，当系统无未知扰动时，由式(8)可知，UIO最优故障诊断观测器退化为全阶Luenberger观测器，这也解释了为什么Luenberger观测器存在的条件只要满足(C，A)可观测，通过比较分析也能看出本节提出了UIO故障诊断观测器对系统的故障诊断更具一般性，当系统存在未知扰动时，可有效地减小干扰对诊断效果的影响，达到鲁棒故障诊断的目的，减小误报、漏报率，对实际系统的应用更具现实意义．

当减摇鳍控制系统满足UIO最优故障诊断观测器设计条件时，设计的故障诊断观测器的状态估计误差方差决定了设计观测器的质量．

状态估计方差阵为

代入状态估计误差式(9)，则

因为CPkCT+Wk为正定阵，所以存在矩阵ζ，满足

基于上述推导，本节给出了减摇鳍控制系统UIO最优故障诊断观测器设计实现流程:1)设置初值P0，由式(3)可知z0=x0-CE(CE)+y0，H0=0，K=0.2)由式(10)计算Hk+1.3)由式(17)计算K1k+1.4)通过解式(8)，计算Tk+1，Fk+1，5)由UIO最优故障诊断观测器结构(3)，计算状态估计k+1及zk+1.6)通过状态估计方差阵式(16)计算状态估计方差Pk+1.7)设置k=k+1，继续下一步计算.

3 故障决策算法设计

残差信号是在故障诊断决策中用来表征故障的待设计信号，因此残差信号设计质量决定了故障诊断的水平，基于模型的故障诊断的核心问题即为残差的设计，结合NJ5型减摇鳍控制系统，考虑实际应用环境以及对船舶航行安全性重要影响，本节利用统计决策规则给出了一种门限阈值设计方法．

构造残差信号为

当系统为无故障状态H0时，由式(19)可知

由式(20)可见，当系统为FAU1时，残差的统计特性与HEA0不同，故障检测的目的就是构建一个决策函数，当决策函数超出预设阈值时，判定系统为FAU1.构造如下故障检测决策函数为

由式(20)的残差统计特性可知，故障检测决策函数服从χ2分布，故障检测逻辑关系为

其中:Jth为故障检测门限阈值，由χ2分布表确定.

当给定系统故障检测误报率指标Pf时，则通过查找χ2分布表，式P［Γk≥Jth｜HEA0］=Pf中故障诊断门限阈值Jth可求.比较逻辑关系式(21)，可判断故障是否发生.

4 仿真验证

为了验证本文提出的UIO最优故障诊断观测器诊断方法(定义为方法1)的效果，以及相比于未考虑干扰解耦诊断方法(定义为方法2)的优越性，本文以NJ5型减摇鳍控制系统为研究对象，在Matlab仿真环境下验证了算法的有效性．

NJ5型减摇鳍控制系统的连续模型如式(1)所示，系统参数为

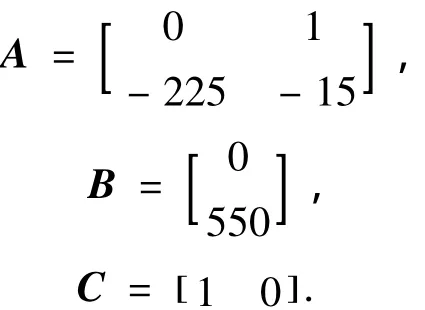
为了方便实际应用实现，采用离散形式的系统模型，如式(2)所示，由F0=eAT，G0=，可知离散形式的系统参数.设系统未知扰动分布阵Wk=0.12I3×3，uk=8，x0=0，故障为

图3～8给出了提出的UIO最优故障诊断观测器的鳍角、鳍角变化率的估计、残差以及传统算法的残差．由图3、4可以看出，在本文的UIO最优故障诊断观测器估计下，得到的鳍角估计误差的绝对值要小于未考虑未知扰动的方法2，在收敛速度上，本文提出的UIO最优故障诊断观测器在15 s左右收敛，而对比于传统的未考虑干扰解耦的故障诊断算法的收敛性差的缺陷，本文提出的算法减小了故障诊断时间，提高了故障诊断效率．图4表征了方法2以及本文算法鳍角变化率估计误差的特性，结果表明，本文算法的收敛性优于方法2，在估计精度上，本文算法提高了鳍角变化率的估计精度．图5描述了系统残差情况，图6为其局部放大图，从图5、6可知，系统残差达到了对未知扰动解耦的目的，解耦后的残差为小量且收敛到零，图7为在假设故障情况下的残差，当给定故障诊断系统性能指标，设定合理门限可实时诊断出故障，为后续容错控制提供保证，对比方法2的残差(见图8)，显而易见，本文算法构造的残差收敛性更好，可以有效地减小故障诊断的误报率．

图3 鳍角估计误差绝对值

图4 鳍角变化率估计误差

图5 本文算法残差

图6 本文算法残差局部放大图

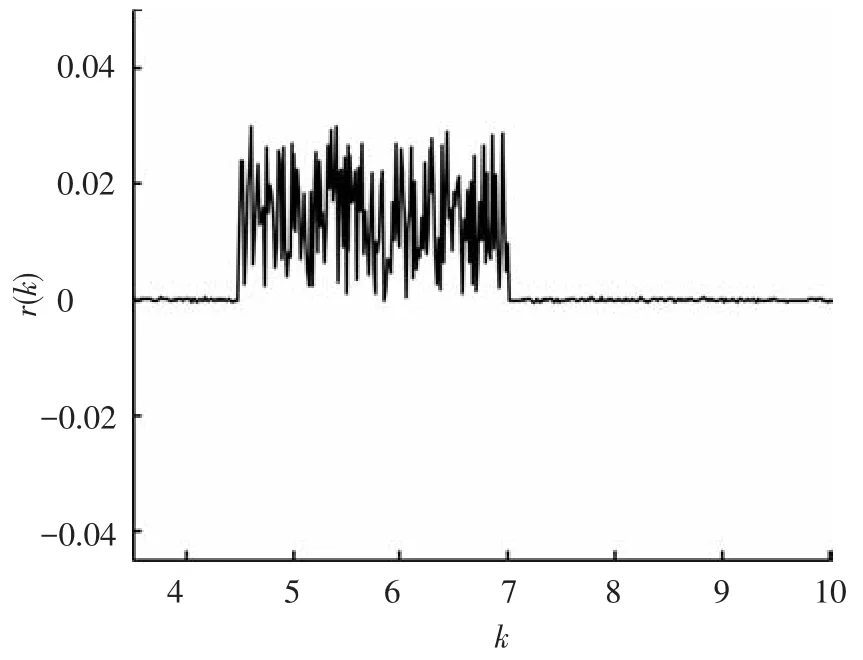
图7 系统故障状态下的残差

图8 方法2残差

5 结论

1)针对减摇鳍控制系统设计了一种UIO最优故障诊断观测器，设计的UIO最优故障诊断观测器相比未考虑未知扰动的诊断方法，得到的状态估计误差小.

2)状态估计误差的收敛性比较，UIO最优故障诊断方法要优于未考虑干扰解耦诊断方法，达到了快速收敛.

3)故障诊断阶段，UIO最优故障诊断方法的残差收敛效果要优于未考虑干扰解耦诊断方法，提出的UIO最优故障诊断方法快速响应了系统出现的故障.

4)减摇鳍控制系统是船舶安全航行的重要保证，提出的算法易于计算机实现，算法结构可靠，适合工程实现.

［1］金鸿章，王帆.零航速仿生减摇鳍水动力模型改进［J］.机械工程学报，2010，46(23):89-92.

［2］金鸿章，高妍南，潘立鑫，等.基于改进积分型变结构控制器的近水面机器人减摇鳍系统［J］.控制与决策，2011，26(4):57-64.

［3］PEREZ T，GOODWIN G C.Constrained predictive control of ship fin stabilizers to prevent dynamic stall［J］.Control Engineering Practice，2008，16(4):482-494.

［4］LEE S K，RHEE K P，CHOI J W.Design of the roll stabilization controller，using fin stabilizers and pod propellers［J］.Applied Ocean Research，2011，33(4):229-239.

［5］WANG Fan，JIN Hongzhang，QI Zhigang.Modeling for active fin stabilizers at zero speed［J］.Ocean Engineering，2009，36(17/18):1425-1437.

［6］SAGER S.Reformulations and algorithms for the optimization of switching decisions in nonlinear optimal control［J］.Journal of Process Control，2009，19(8):1238-1247.

［7］LOGIST F，SAGER S，KIRCHES C，et al．Efficient multiple objective optimal control of dynamic systems with integer controls［J］.Journal of Process Control，2010，20(7):810-822.

［8］NHAN T N.Optimal control modification for robust adaptive control with large adaptive gain［J］.Systems＆Control Letters，2012，61(4):485-494.

［9］DANIEL E M.A new approach to adaptive control:no nonlinearities［J］.Systems＆Control Letters，2003，49(1):67-79.

［10］QI Ruiyun，MIETEK A B.Stable indirect adaptive control based on discrete-time T-S fuzzy model［J］.Systems＆Control Letters，2003，49(1):67-79.

［11］BOULKROUNE A，TADJINE M，M’SAAD M，et al．Fuzzy adaptive controller for MIMO nonlinear systems with known and unknown control direction［J］.Fuzzy Sets and Systems，2010，161(6):797-820.

［12］DALY J M，WANG D W L.Output feedback sliding mode control in the presence of unknown disturbances［J］.Systems＆Control Letters，2009，58(3):188-193.

［13］GOUAISBAUT F，DAMBRINE M，RICHARD J P.Robust control of delay systems:a sliding mode control design via LMI［J］.Systems＆Control Letters，2002，46(4):219-230.

［14］EDWARDS C，TAN C P.Sensor fault tolerant control using sliding mode observers［J］.Control Engineering Practice，2006，14(8):897-908.