大跨斜拉桥预应力索塔锚固区受力机理及试验

叶华文，肖 林，李翠娟，徐 勋，强士中

(西南交通大学土木工程学院，610031成都)

近几十年来，大跨混凝土主塔斜拉桥在我国蓬勃兴起，其跨径已突破千米，如苏通长江大桥(主跨1 088 m)和香港昂船洲大桥(主跨1 018 m)，斜拉索设计索力也超千吨级.大跨斜拉桥索塔锚固区是将主梁自重和所承担的外荷载传递到主塔的重要构造，其受到强大的索力作用，因此确保锚固区安全对主塔，乃至全桥都至关重要.大跨斜拉桥主塔很多采用预应力混凝土箱形断面，既充分发挥混凝土的材料特性，又通过施加环向预应力来平衡斜拉索对塔壁产生的强大拉力，保证索塔锚固区有足够的抗裂性和承载力.

项贻强等［1-2］和刘钊等［3］进行了实桥索塔锚固区模型试验，陶齐宇［4］提出了拉压杆分析模型，苏庆田等［5］建立钢混组合锚固区索力分配计算模式，国外一些学者［6-7］也进行了索塔锚固区理论分析和参数化研究，表明了索塔锚固区水平受力(垂直于塔轴线的受力)是控制因素;但是，很多有限元模型［8］和理论分析［9］主要基于单个工程的有限元分析，缺乏简便的初步估算和设计预应力的研究，大多数模型试验［10-11］采用水平加载来模拟斜拉索荷载，有些为缩尺模型［12-13］，与实际斜向受力状态相比，在受力特性、结构空间应力分布等方面，存在一定差距.本文针对预应力索塔锚固区构造的特殊性和复杂性，结合实际工程，采用理论推导和斜向加载的足尺模型试验的方法，着重讨论了不同受力阶段锚固区受力机理、应力分布以及简化分析方法，为大跨斜拉桥的预应力索塔锚固区分析和设计提供参考.

1 理论分析模型

1.1 模型说明及假定

对索塔锚固区进行受力分析时，由于结构复杂往往采用实体有限元单元进行计算，不易被一般工程设计人员使用，一种简化的分析和计算方法是必要的.从实际索塔结构到简化分析模型需对结构进行适当的假定:

1)平面框架模型.根据文献［4］的总结，大多数桥塔塔壁长度与厚度之比均大于2，故可采用框架结构分析.已有研究成果表明，水平力(垂直于塔轴线的力)控制索塔锚固区受力行为，因此以索塔水平受力为分析对象，将索塔截面简化为平面框架结构，如图1(a)所示，取混凝土塔壁的中心线作为框架结构的外部尺寸，忽略混凝土塔壁隅角处的局部截面变化，框架四角为刚性角.

2)竖向受力范围.主塔竖向上索力作用范围简化为拉索水平分力45°均匀扩散，如图1(b)所示，索力传递到该范围内(定义高度范围为h)的预应力筋和混凝土塔壁上.

3)索力荷载对称.锚固区左右两边斜拉索的水平分力一般不相等，但相差不大.偏于安全，取较大水平分力代替较小的水平分力，使得左右荷载对称.

4)预应力均布.由于预应力钢绞线竖向间距较小，可认为预应力竖向上均布.

5)索塔横截面对称.索塔平面框架模型可以按正对称模型简化，只取图1所示1/4平面结构进行分析.

分别按预应力张拉和仅索力作用两个阶段来分析其受力情况，如图2所示，然后迭加两个阶段受力就可以得到成桥运营阶段的受力情况.

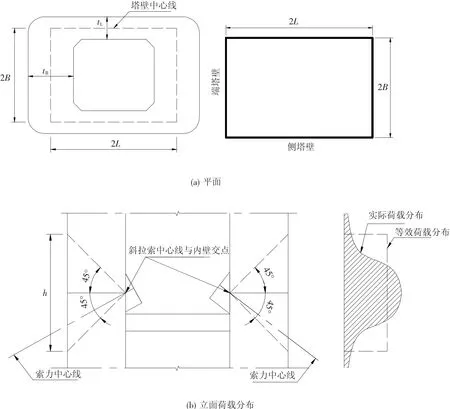
图1 平面框架简化分析模型

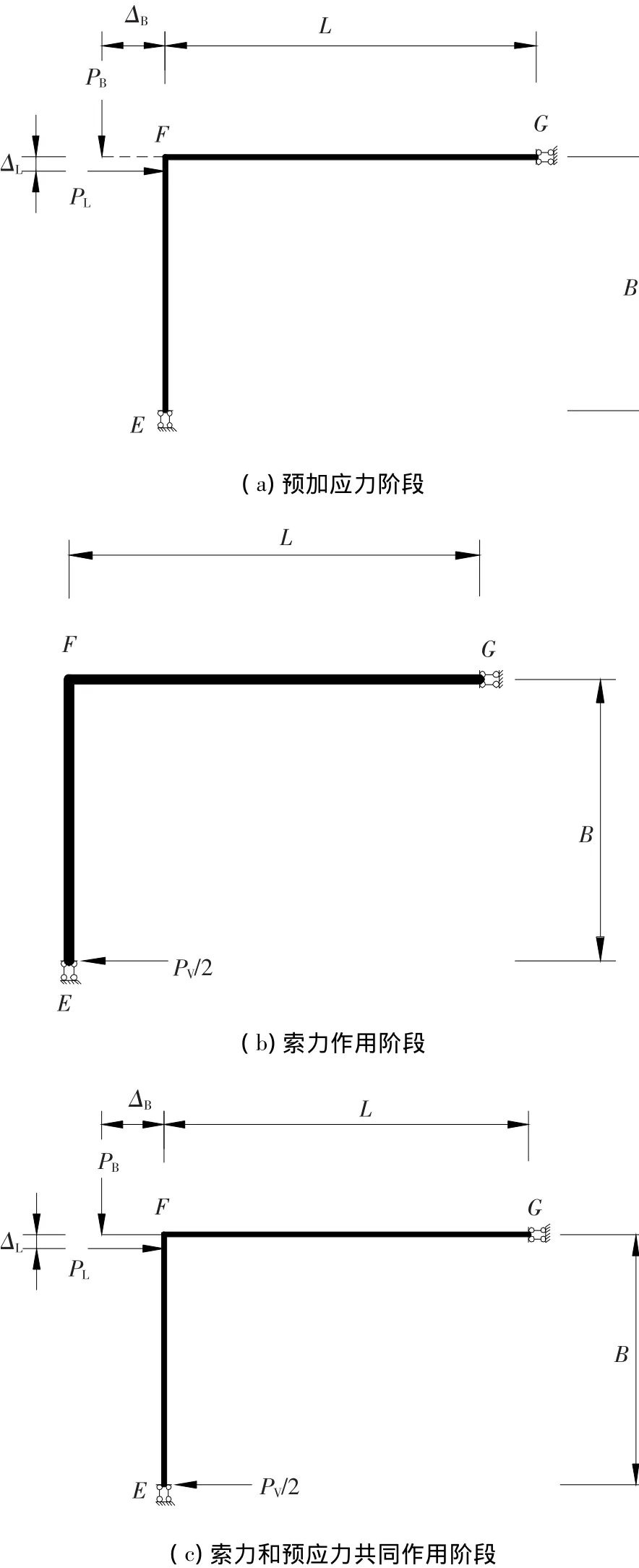
图2 计算分析模型

1.2 理论计算

PL和PB分别为作用于侧塔壁和端塔壁中部截面上的有效预应力荷载，PV为作用于端塔壁的索力水平分力;端塔壁(短边)和侧塔壁(长边)的中心线距离分别为2B和2L;tB和tL为端塔壁和侧塔壁的厚度;ΔL和ΔB为预应力筋作用线偏离混凝土塔壁中心线的距离;h=2tB，如图1所示．

在预加应力阶段，结构处于弹性阶段，根据经典结构力学方法，按线刚度进行分配(设刚度比为η)可得到端塔壁中部E点处和侧塔壁中部G点处弯矩MB1和ML1分别为

预应力张拉锚固后，端塔壁中部E点处和侧塔壁中部G点处应力σB1和σL1分别为

同理可得到仅斜拉索水平分力作用阶段，端塔壁中部E点处和侧塔壁中部G点处弯矩MB2和ML2分别为

因此在索力作用阶段，端塔壁中部E点处和侧塔壁中部G点处应力σB2和σL2分别为

综上可得索力和预应力共同作用阶段，端塔壁中部E点处和侧塔壁中部G点处应力σB和σL分别为

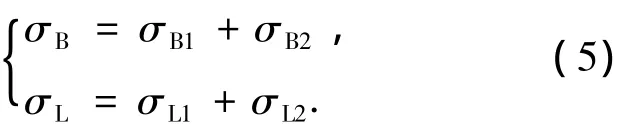
由理论分析模型可知:在预应力施工阶段，端塔壁内侧和侧塔壁外侧容易出现拉应力;索力和预应力共同作用阶段，端塔壁外侧和侧塔壁内侧容易出现拉应力.根据公路桥梁规范的规定，混凝土的拉应力应不超过其容许拉应力［σ］，即有预应力阶段:

索力和预应力共同作用阶段:

根据式(6)、(7)可简便计算所需预应力和评估锚固区的受力性能，以上推导基于假设钢材和混凝土均处于弹性状态，因为正常使用情况下塔壁混凝土处于弹性工作状态，不产生裂缝.

2 试验设计

2.1 试验概况

为研究预应力索塔水平方向受力机理，结合实际工程进行了足尺模型试验.根据内力等效原则和圣维南原理，为尽可能减小整体位移边界条件对索塔锚固区节段的影响，同时考虑到试验锚索的相对位置，节段以斜拉索作用线中心分别向上向下延伸一定距离，以保证结构应力分布受模拟边界条件影响较小.取模型节段高度为3 m，截面尺寸(5.3 m×3.6 m)跟实桥主塔尺寸一致，节段下部固结于预应力混凝土矩形底梁作为边界条件，试验模型见图3，两端斜拉索分别为S和M端.试验节段模型制造工艺和材料性能要求均与实桥一致.通过自平衡体系进行千斤顶加载，分别在试验模型两侧各张拉两束拉索至所需荷载水平.模型混凝土强度等级为C55.试验节段内共设10层(竖向间距37.5 cm)共20束(U形12束Φs15.2-12和直线形8束Φs15.2-9)预应力束筋，标准强度为1 860 MPa，预应力束曲率半径R为1.4 m.U型筋采用两端张拉，张拉控制应力σcon=1 302 MPa.根据实测，预应力管道摩擦系数取μ=0.25，管道偏差系数k=0.001 5，其他损失参照规范计算.

图3 索塔锚固区试验方案

2.2 实体有限元模型

三维空间结构分析是全面了解锚固节段结构应力分布的重要手段，依据模型试验施工图建立三维空间实体有限元计算模型，模型包含锚固齿块、斜拉索导管等构造细节，见图4.主体结构采用solid45单元，对拉索导管附近区域的网格做了细化处理，预应力筋采用link单元，采用降温法施加预应力.理论模型和有限元模型有效预应力均为800 MPa.

2.3 加载工况

试验加载工况根据不同受力阶段分为3种:1)工况一(预应力施工锚固阶段)，直线筋采用一端张拉，U形筋采用两端张拉，张拉控制应力σcon=1 302 MPa，施工顺序为先张拉U形筋(6根，加载序号为1～6)，后直线筋(4层，加载序号为7～10);2)工况二(正常使用阶段)，锚固区S和M两端同时施加1倍设计索力荷载P(1 330 t)，加载程序见表1;3)工况三(断索阶段)，锚固区只S端施加索力设计荷载，以研究在断索状态下锚固区受力情况，加载程序见表2.

图4 试验有限元模型

表11 倍设计荷载加载程序

表2 非对称加载程序

2.4 应变测试及裂缝观测

试验节段分区分层布置三向应变片，平面上塔4个边分为A、B、C、D区，W和N分别为外和内表面，内外面应变片基本上一一对应;竖向从顶面到底面分为4层:0、1、2、3;横向从左至右编号，见图5、6.另外，在模型内部钢筋骨架上亦对称布置了少量应变片.在混凝土的外表面画出方格线，利用裂缝观测仪观测每级荷载作用下有无裂缝展开及各控制荷载下的裂缝分布情况.长度单位除特殊说明均为cm.

图5 索塔节段测区分布

图6 索塔节段立面各测区测点分布

3 试验结果分析与讨论

3.1 预应力施工阶段

预加应力阶段各关键测点实测应力值与理论值、空间有限元分析结果比较见表3，应变均以压为负，以拉为正.通过对比可见:预加应力完成后，各测点实测水平预压应力值普遍小于或接近理论分析值，究其原因，一方面，由于实际模型施工中预应力筋的位置与设计孔道存在一定偏差，预应力筋张拉后实际有效的预加应力与理论计算值也不一定完全相等;另一方面由于实际的索塔节段模型其截面特性与有限元分析和理论公式采用的理想化模型也存在一定差异，如锚固区齿块增加了刚度，这一点对模型的端塔壁影响尤为突出.

由表3可见，主塔锚固区水平预压应力在不同高度有一定差异，在实测值和有限元值中得到体现.由于理论值是一个简化计算公式，数值偏保守，也无法考虑高度上的应变变化，因此可作为设计锚固区预应力的简便公式使用.预应力作用下端塔壁有向内压缩的变形，而侧塔壁有向外凸出的变形，从而在相应位置产生拉压应变.

由表3可见，实测值与计算值(有限元值和理论值)较为接近，且均小于计算值，说明结构是安全的.理论值在端塔壁外侧偏大，结果偏保守，主要是齿块增大了端塔壁刚度，减小了应力.

表3 预压应力值比较分析MPa

3.2 正常使用阶段

正常使用阶段下，设计索力为1 330 t，主塔各关键点荷载-水平应变曲线见图7，应变与荷载的比例基本不变，并且在1倍索力设计荷载(1 330 t)作用范围内，大部分测点的荷载-水平应变关系呈线性，反映出这些测点附近的混凝土处于弹性状态;个别测点荷载-水平应变曲线直线性不理想，可能因应变较小，测量误差等原因.

图7 主塔关键点荷载-水平应变曲线

表4为关键测点实测值与预测值的比较分析，当荷载在1 330 t时，实测应力值普遍接近或小于有限元理论分析值，主要因为实际的节段模型由于非预应力筋配置较为充足，其整体刚度要比有限元分析模型的大所致.少数点实测值与理论值偏差较大，可能是测量误差缘故.总体说，试验是成功、可靠的，提出的理论分析模型可以简便评估锚固区受力情况.图8所示为试验节段高度方向上塔壁中部的应力分布(MPa)，可见:索力主要由锚固区齿块附近一定范围内承担，超过这个范围应力急剧下降，与理论模型的假设2)是符合的.选取塔壁关键点进行正常使用阶段应力分析，见表5.

图8 设计索力作用下A-W面中部高度方向水平应力分布

端塔壁外侧关键点在预应力和1倍设计索力作用下分别产生的最大应力增量为-1.9 MPa和2.55 MPa，相叠加后有0.66 MPa拉应力;侧塔壁内外侧在正常使用状态还有相当大预压应力存在，这些结果说明正常使用阶段索力水平分力由环向预应力筋承担，侧塔壁混凝土作安全储备，承担很少，因此预应力筋有效预应力值大小在设计和施工中应足够重视.

表4 索力作用下水平应力增量比较分析MPa

表5 正常使用阶段实测应力分析MPa

3.3 断索阶段

断索阶段为非对称加载工况，主塔S端塔壁外表面和侧塔壁内表面高度方向各关键点荷载-水平应变曲线见图9，主要受力模式如图中粗线所示，水平应变与荷载的比例基本呈线性关系.图9(a)表明:主塔S端塔壁外表面各测点应变在加载级6～11之间基本不变，此时M端处于卸载状态，说明一端索力对另一端锚固区只是提供了反力，一端断索后对另一端锚固区受力影响不大，此时反力由索转换为塔本身承担.图9(b)表明，主塔侧塔壁外表面各测点应变在加载级6～11逐级下降，M端卸载时侧塔壁也在卸载，说明S端索力由侧塔壁承担转换为节段底部剪力承担，一端断索对侧塔壁是卸载作用.

图9 主塔高度方向关键点荷载-水平应变曲线

4 结论

1)预应力混凝土索塔锚固区简化成平面框架模型，可得用于索塔水平受力机理的简化计算公式.通过与足尺模型试验结果和有限元结果对比，证明所提简化模型力学概念明确，简单实用，可用于预应力混凝土索塔锚固区受力分析和预应力筋设计.

2)对预应力混泥土索塔锚固区，斜拉索水平力主要由环向预应力筋承担，混凝土塔壁承担的拉索水平力很小，因此预应力筋有效预应力值应满足规范要求，以免混凝土开裂.

3)试验结果表明，一端断索后对另一端锚固区受力影响很小，因此所提简化模型经适当调整，仍可用于非对称索力作用情况.

［1］项贻强，易绍平，杜晓庆.南京长江二桥南汊桥斜拉索塔节段足尺模型的研究［J］.土木工程学报，2000，33(1):15-22.

［2］项贻强，陈国强.鄱阳湖口大桥索塔节段足尺模型试验与分析研究［J］.中国公路学报，2000，13(10):74-78.

［3］刘钊，孟少平，刘智.润扬大桥北汊斜拉桥索塔节段足尺模型试验研究［J］.土木工程学报，2004，37(6):35-40.

［4］陶齐宇.大跨度斜拉桥预应力混凝土索塔关键问题研究［D］.成都:西南交通大学，2012.

［5］苏庆田，秦飞.组合索塔锚固区水平受力机理的理论与试验［J］.同济大学学报:自然科学版，2011，39(8):1120-1125.

［6］JO B W，BYUN Y J，TAE G H.Structural behavior of cable anchorage zones in prestressed concrete cablestayed bridge［J］.Canadian Journal of Civil Engineer，2002，29(1):171-180.

［7］HENPRATHANEES.Linear and nonlinear finite element analysis of anchorage zones in post-tensioned concrete structures［D］.Blacks-burg:Virginia Polytechnic Institute and State University，2004.

［8］张晋，杨小敬，张建，等.索塔节段足尺试验及其全过程仿真分析［J］.土木工程学报，2010，43(增刊):158-163.

［9］陈开利.钢锚箱索塔锚固区受力机理［J］.中国铁道科学，2008，29(4):58-64.

［10］钟继卫，黄展军，王波，等.扭背索斜拉桥非对称索塔锚固区足尺模型试验研究［J］.世界桥梁，2011(4):45-48.

［11］刘世建.井字型预应力体系在索塔锚固区的应用及试验研究［D］.重庆:重庆交通大学，2008.

［12］刘兆丰，孟鑫，赵人达，等.长寿长江公路大桥索塔节段足尺模型试验研究［J］.公路交通科技，2009，26(8):77-83.

［13］单炜，李玉顺，于玲，等.异形截面斜拉桥索塔锚固区节段足尺模型试验研究［J］.中国公路学报，2005，18(3):60-65.