流化床气化炉气固两相流三维数值模拟

张 锐

(东北电力大学能源与动力工程学院，吉林 吉林 132012)

流化床技术被广泛应用于燃料的燃烧、热解、气化等工业过程，流化床内气固两相的流动特性已成为人们研究的重点[1-3]。流化床反应器气固两相间的接触表面状态变化较快，颗粒大小、形状、密度、气流速度和湍流强度等都会对流化床内气固两相流动特性产生一定影响[4]。因此，为了掌握流化床气化炉的工作性能，人们对流化床技术进行了大量的研究。L.P.Cammarate[5]应用 CFX4.4软件进行了矩形鼓泡流化床的2D与3D数值模拟的比较;Darton RC LR[6]通过2D与3D的流化床数值模拟，得到床层膨胀、气泡尺寸与气泡上升速率等结果;K.Papadikis[7]应用 Fluent 6.2 进行了流化床的 2D与3D模拟，计算了施加在颗粒上的力与颗粒的速度矢量图，结论表明3D数值模拟对于预测流体动量、质量与能量的传递更为准确。本文应用CFD软件Fluent进行流化床内气固两相流数值模拟，并通过上述文献整理选择适合流化床气固模拟的参数设置，进行流化床内气固两相流的三维模拟及对模拟结果进行分析，研究流化床内颗粒的流动特性。

1 计算模型及数值方法

1.1 数值模拟方法及控制方程

目前气固两相的数值模拟方法可分为欧拉-拉格朗日方法和欧拉-欧拉方法。欧拉拉格朗日方法计算量大，颗粒数量要小于106，通常应用于机理研究。欧拉-欧拉方法将气固两相均视为连续相，结合颗粒动力学进行求解[8]，颗粒的脉动动能可用颗粒温度来表示，颗粒脉动在颗粒相中形成有效压力、有效粘度，二者均取决于颗粒温度。本文选用欧拉-欧拉双流体模型结合颗粒动力学进行数值模拟。

大量文献研究了曳力模型对气固两相流流动特性的影响。M.Syamlal[9]的研究表明，Syamlal-O’Brien曳力模型对床层压降、床层膨胀与气泡直径的预测值偏低。李东耀[2]基于Fluent软件进行了流化床内气固两相流模型研究，结果表明Gidaspow曳力模型与流态化原理及文献结果吻合性较好。本文采用Gidaspow曳力模型。

1.2 几何模型、边界条件与网格划分

图1为流化床反应器结构示意图。流化床直径为0.05 m，为了减少网格数，节省计算时间，模型选择布风板上部0.5 m的空间进行建模及网格划分。空气从流化床下部流入，边界条件为速度入口，从流化床上部流出，边界条件为压力出口，压力大小为101.3 kPa。采用控制容积法离散控制方程，孔隙率选用QUICK格式，以提高计算精与相界面清晰度，其余物理量采用一阶迎风差分格式获得，流体压力–速度耦合基于Simple算法。利用Gambit软件进行流化床的三维结构体网格划分，建立总网格数为 20 000、40 000、60 000、80 000 的流化床模型，进行网格无关性验证。结果表明:当网格数大于40 000后，网格数目的增加对数值模拟的结果影响较小。最终选用总网格数为40 000的流化床模型进行数值模拟。

图1 流化床网格划分

计算中的气相选用标准状态下的空气，颗粒相为沙子，颗粒的平均直径为0.5 mm，沙子真实密度为2 300 kg/m3，堆积密度为1 380 kg/m3，颗粒堆积静止高度为0.2 m，初始固含率为0.6。

2 数值模拟结果及分析

2.1 初始流化过程固含率分析

图2为0～1 s内轴向截面颗粒固含率分布图。从图2可以看出，床层从初始状态的静止到稳定流化的过程。随着空气不断涌入炉膛，床层不断膨胀，颗粒固含率不断减小。在气泡的上升过程中，气泡间发生融合，在压力下降等因素的作用下，气泡被拉长，冲出床层后破裂，最终回落。

图2 轴向截面固含率云图

图3为图1相应的3D固含率等值面图(颗粒固含率ε=0.3)。由图3可以看出，空气涌入后，气泡界面向上移动。在初始流化过程中，气泡截面呈现为一个近似对称的4个尖峰向炉膛上方运动(t=0.5 s)，推动静止床料向上膨胀，最终冲出床层(t=0.7 s)。经过最初的1 s后，流化床内形成稳定的气泡，床层开始稳定流化。

图3 轴向截面固含率等值面图(颗粒固含率ε=0.3)

2.2 流化床瞬时固含率及流场分析

流化床模拟过程为0～6 s，本文分析第5.6 s的瞬时流场、径向(轴向)固含率分布云图、颗粒速度矢量图、5.8 s的单个气泡轴线固含率云图、固含率等值线图。

2.2.1 轴向固含率及颗粒流场分析

图4a、4b为5.6 s时刻轴向颗粒固含率云图及速度矢量图。由图4可知，在5.6 s时刻，流化床内处于稳定的流化状态，颗粒在床体内的分布整体呈现为上稀下浓、近壁面固含率高、中心固含率低的分布特点，颗粒在炉膛中心区域速度较高且方向向上，而在靠近壁面的地方速度较低且沿壁面向下运动。图4c为5.6 s时刻颗粒流线图，可以看出颗粒瞬时的运动状态。颗粒呈现出“壁面—中心—壁面”运动趋势，形成炉膛内部的内循环。

图4 5.6 s轴向截面固含率分布云图、颗粒速度矢量图及颗粒流线图

2.2.2 径向固含率及颗粒流场分析

图5a、5b为5.6 s时刻(z=0.05 m，z=0.10 m，z=0.15 m，z=0.20 m，z=0.25 m，z=0.30 m)5 个截面的固含率云图及颗粒速度矢量图。由图5a可以看出，在径向方向上，颗粒固含率在流化床中心区域较稀，靠近壁面固含率较高。随着高度的增加，颗粒的固含率呈现逐渐减小的趋势，颗粒浓度呈现出“上稀下浓”的分布。从图5b的颗粒速度矢量图看出，近壁面的颗粒向下运动且速度较小，而在中心区域的颗粒向流化床上部运动且运动速度较快，结合轴向颗粒固含率分布图及颗粒速度矢量图，表明颗粒在流化床内呈现出典型的“环—核”流动。

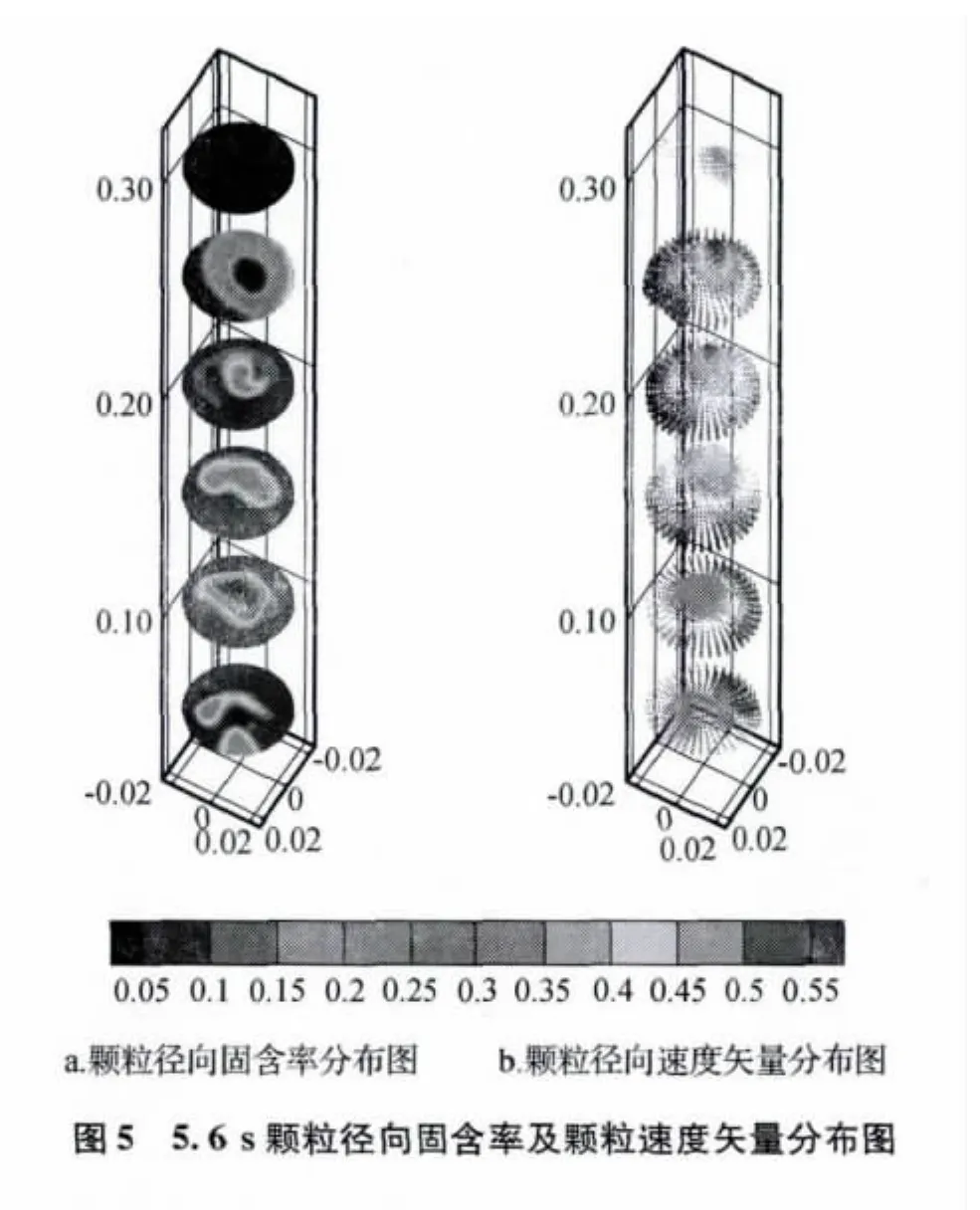
2.3 单个气泡颗粒运动

图6a为5.8 s的Y-Z截面的固含率等值线图，图6b为颗粒固含率0.3等值面围成的气泡及等值面上的颗粒速度矢量图，箭头表示颗粒的速度矢量。可以看出，在固含率小于0.1的气泡中，颗粒速度较小，处于悬浮状态。在颗粒悬浮区域的上部，颗粒向炉膛上方涌动，在气泡的作用下，颗粒速度越来越快。而在悬浮区域的下部，气泡中存在的少量颗粒在自身重力及气体曳力的作用下向下运动。在底部尾涡的低压区中，较多的颗粒进入气泡内部，并在气泡的左右两侧流出。综上所述，颗粒在气相的曳力与自身的重力下运动，在尾涡的作用下从气泡尾部大量进入，在气泡的两侧流出。在气泡运动的作用下，颗粒在流化床内完成内循环。

3 结论

本文应用CFD软件Fluent、双流体模型模拟实验鼓泡流化床内的气固流动，并通过分析颗粒初始流化过程、颗粒瞬时的轴向径向固含率、颗粒速度矢量、单个气泡周围颗粒的速度矢量，得到以下结论:

1)在初始流化过程中，气泡沿壁面呈环状尖峰向上部空间涌入，推动床层膨胀，使颗粒稳定流化。

2)颗粒在轴向呈现上稀下浓的分布状态，在径向方向，近颗粒在壁面浓度高、运动方向向下且速度较低，而在炉膛中部颗粒浓度低、运动方向向上且速度较高。颗粒呈现由“中心—壁面—中心”的流动状态。

3)在固含率小于0.1的气泡中，颗粒速度较小，处于悬浮状态，在悬浮区域上部，颗粒向炉膛上部涌动。在底部尾涡的低压区中，较多的颗粒进入气泡内部，并在气泡左右两侧流出，颗粒在流化床内呈现出典型的“环—核”流动。

[1]王建军，李东芳，姬广勤，等.循环流化床锅炉炉膛内气固两相流的数值模拟[J].锅炉技术，2010，41(3)，21-26.

[2]李东耀.基于Fluent软件的流化床的气固两相流模型研究[D].重庆:重庆大学，2009.

[3]张腾.循环流化床气固流动冷态数值模拟[D].北京:华北电力大学，2011.

[4]H.R.M.Hanzehei.Experimental and numerical study of hydrodynamics withheat transfer in a gas-solids fluidized-bed reactor at different particle sizes[J]，Ind.Eng.Chem.Res 2009，48(6)，3177-3186.

[5]L.P.Cammarate L，Micale DMG，Colman D.2D and 3D CFD simulations of bubbling fluidized beds using Eulerian-Eulerian models[J]，Int J Chem React Eng，2003，1，A48.

[6]L.R.Darton RC，Davidson JF，Harrison D.Bubble growth due to coalescence in fluidised beds[J]，Trans Am Inst Chem Eng，1977，55，274-280.

[7]K.Papadikis，A.V.Bridgwater，S.Gu.CFD modelling of the fast pyrolysis of biomass in fluidised bed reactors，Part A:Eulerian computation of momentum transport in bubbling fluidised beds[J]，Chemical Engineering Science，2008，63(16)，4218-4227.

[8]J.Ding，D.Gidaspow，A bubbling fluidization model using kinetic theory of granular flow[J]，AIChE，1990，36(4)，523-538.

[9]T.J.O.B.M.Syamlal.Computer simulation of bubbles in a fluidized bed[J]，AIChE，1989，47，22-31.