换流变压器绕组辐向短路电动力的计算与分析

马 健，刘文里，王录亮，钟 燕

(1.哈尔滨理工大学电气与电子工程学院，哈尔滨 150080;2.海南电力技术研究院，海口 570203)

在直流输电系统中，换流变压器承担着电功率的传送、电压的交换以及交直流系统的隔离等任务[1]。随着我国直流输电工程的不断发展，换流变压器的安全可靠性越来越受到关注。因此，研究换流变压器的相关问题具有重要意义。

绕组辐向失稳是造成大容量变压器损坏的重要原因[2]。由于换流变压器结构与普通电力变压器有所不同，目前对其研究的资料还不是很多，关于辐向短路力问题的报道更是少见。虽然近年来国内外学者利用数值法对有关变压器绕组短路力进行了许多研究[2-5]，但都局限于普通电力变压器。为此，本文以一台单相双绕组换流变压器为例，在网侧绕组处于+9×1.25%分接的情况下，基于“场-路耦合”法建立了阀侧绕组发生短路工况时的2D有限元模型，通过对短路阻抗计算值与实测值的比较，验证了所建模型及计算方法的可行性。

1 计算原理

1．1 换流变压器技术特点概述

大容量直流输电系统采用的换流变压器一般为单相双绕组结构[6]。铁心采用单相四柱式，由铁心向外依次为调压绕组、网侧绕组、阀侧绕组。

换流变压器工作原理与电力变压器相同，但在绝缘、谐波、试验和直流偏磁等方面有所不同[7]。网侧绕组的主、纵绝缘设计和普通电力变压器基本相同。由于调压级数多，调压绕组通常设计成一个独立的绕组。阀侧绕组采用全绝缘设计，通过阀侧套管与换流阀桥联接。阀侧绕组主、纵绝缘设计除了要考虑交流耐受电压的作用外，还必须考虑试验及运行中的直流电压和极性反转电压作用的影响，这是换流变压器与普通电力变压器结构上不同的根本所在。此外，直流偏磁现象会导致铁心中损耗和噪声大幅度升高;负载电流中含有大量的高次谐波分量，在绕组和金属结构件中产生谐波漏磁场与高次谐波损耗，造成换流变压器内部局部过热。

1．2 漏磁场分析

单相双绕组换流变压器的漏磁通是由阀侧绕组的安匝和与之相平衡的网侧绕组安匝负载分量共同产生的[8]。由于其绕组结构的特殊性，因此本文仅考虑网侧绕组处于+9×1.25%分接情况，即独立调压绕组并未参与运行。

绕组中通有电流时，将在绕组周围产生漏磁场。在网、阀侧绕组所占据的空间里，漏磁场可以分解为轴向分量与辐向分量，这两个分量与绕组中的电流相互作用，将在绕组内产生电动力。

网、阀侧绕组的磁势相互平衡，产生的纵向漏磁通贯穿流过两绕组所占据的全部空间。可以假设绕组空间内磁力线是竖直的，忽略其周围空间的磁阻及以外磁路的磁压降，简化后的单相双绕组换流变压器绕组纵断面及纵向漏磁分布如图1所示。

图1 绕组纵断面及纵向漏磁分布

该变压器仅有一个纵向漏磁组，网、阀侧绕组横向安匝的平衡程度决定着换流变压器横向漏磁通。

工程上，网、阀侧绕组主漏磁空道处最大漏磁密度的计算公式为

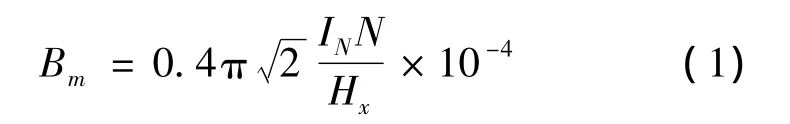
式中:N为安匝数;Hx为绕组电抗高度，cm。

通过式(1)可以计算主漏磁空道各点的漏磁密度，为仿真分析提供理论依据。

1．3 “场-路耦合”法

“场-路耦合”法是在电磁设备内部采用场的方法，外部采用电路参数的方法。通过此方法，可以方便求解出换流变压器阀侧绕组短路时的电磁特性，且根据电路参数的不同，可模拟设备的不同运行情况[9]。

短路模型创建时，把各线饼区域中的一个节点作为电路中的节点来实现耦合，通过外部电路给网侧绕组施加电压载荷，从而将线饼元件分别与网侧所加的电压和阀侧所带的负载相互串联形成闭合电路，如图2所示。图2中，NN1∶NNn为相互串联的网侧绕组各线饼，加电压u1(t);NV1∶NVm为相互串联的阀侧绕组各线饼，端电压为u2(t)，由于阀侧绕组短路，因此所接阻抗大小为零。

图2 换流变压器“场-路耦合”模型

网侧绕组边值问题表达式为

式中:Ak，Jk，NNk，Kk，Sk，ek，lk，Rkσ，Lkσ分别对应网侧绕组第k个线饼的向量磁位、电密、匝数、填充系数、截面积、感应电动势、长度、等效电阻及等效漏电感;n为网侧绕组线饼总数;u1(t)为网侧绕组外接电压源。

阀侧绕组边值问题表达式为

式中:Ai，Ji，NVi，Ki，Si，ei，li，Riσ，Xiσ，Liσ分别对应阀侧绕组第i个线饼的向量磁位、电密、匝数、填充系数、截面积、感应电动势、长度、等效电阻、等效漏电抗及等效漏电感;m为阀侧绕组线饼总数;Zσ为阀侧绕组漏阻抗;u2(t)为阀侧绕组端电压。

对于油区域

将式(2)～(4)离散处理，可得到“场-路耦合”有限元方程为

式中:A、I、E分别对应节点向量磁位矩阵、电流矩阵、电动势矩阵;KAA为向量位刚度矩阵;Kii为电阻刚度矩阵;KAi为磁位-电流耦合刚度矩阵;CiA为电感阻尼矩阵;Kie为电流-电动势耦合刚度矩阵;U0为外加电压矩阵。

由式(5)可得网、阀侧任意节点不同时刻的自由度，即网侧各线饼的电流、磁位，阀侧各线饼的电流、磁位、感应电动势及阀侧绕组端电压。

2 实例分析

基于ANSYS有限元仿真分析，以一台实际运行的530 kV/405.2 MVA单相双绕组换流变压器为例进行计算，其主要参数如表1、表2所示。

表1 换流变压器基本参数

表2 换流变压器绕组参数

2．1 建立模型

根据换流变压器的磁路情况，采用2D有限元分析不仅能基本真实地反映实际漏磁场的分布情况，而且提高了计算速度。针对换流变压器的结构特点，作如下假设条件:

1)根据换流变压器结构和磁路的对称性，取一个心柱上绕组的一半作为求解区域，同时忽略不同心柱绕组间的漏磁影响。

2)不考虑导线涡流的去磁作用，并假定铁磁材料的磁导率为无穷大。

3)忽略励磁电流，网、阀侧绕组的总安匝平衡，且认为每个线饼内的电流密度均匀分布。

4)忽略位移电流的影响，假定绕组铜线的电导率为常数。

5)忽略铁心拉板、夹件等对漏磁场的影响。

为了保证计算结果的准确性，各绕组线饼尺寸、饼间油道尺寸、每个线饼的匝数及填充系数均按实际情况考虑。由于仅对绕组进行分析，故没有对铁心和铁轭进行建模，如图3所示。其中，网、阀侧绕组线饼号自下而上分别为1-162、163-356号。由于模型边界为高导磁材料，因此第二类边界条件可自动满足[10]。

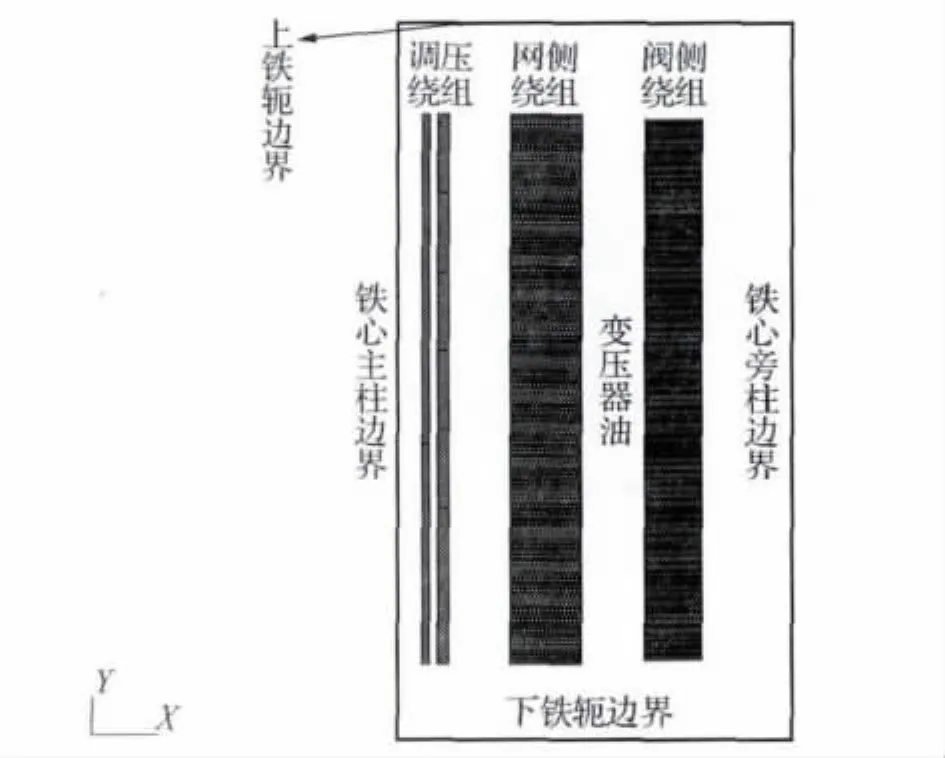
图3 二维轴对称简化模型

2．2 加载与求解

使用ANSYS软件分饼建立换流变压器二维“场-路耦合”有限元模型时，需注意以下事项:

1)由于每个线饼有唯一的电流和电势降，必须把有限元区域中线饼上所有节点的CURR自由度和EMF自由度都耦合起来，且每组耦合都需要唯一的耦合编号。

2)电磁区域中需定义线饼的实常数，即截面积、匝数、填充系数及电流方向。当线饼处于电路区域时，实常数则能反映电路元件参数大小。

当t=0时刻，令图2中网侧电压u1(t)为相电压峰值，选择瞬态分析方法来模拟阀侧绕组短路工况。软件会根据所求的激励电流，通过处理后获得绕组漏磁场分布及各个线饼的洛伦兹力。

3 数值求解结果及分析

3．1 短路阻抗计算

在网侧绕组处于+9×1.25%分接的情况下，短路阻抗实测值与“场-路耦合”法的计算值分别为20.3%和20.15%。可以看出，短路阻抗计算值与实测值的偏差仅有-0.738 9%，说明采用绕组分饼建立有限元模型及其计算方法对换流变压器是合理的，可利用其进行下一步分析。

3．2 短路电流与漏磁场分布

换流变压器网侧绕组处于+9×1.25%分接时，网、阀侧绕组短路电流变化曲线如图4所示。

图4 短路电流峰值随时间的变化情况

绕组短路瞬间属于瞬变过程，短路电流由周期性变化的强制分量和按指数衰减的自由分量组成。可以发现，自由分量的存在导致短路电流曲线不再与时间轴对称，而是随着直流衰减分量的降低逐渐趋于正弦变化。从图4还可看出，网、阀侧短路电流峰值在t=0.01 s时刻达到最大值，分别为8 239.01 A与-28 242 A，是所对应分接电流峰值的9.79、9.78倍，决定着换流变压器机械上的动稳定性。

图5为阀侧绕组短路发生0.01 s时，网侧绕组处于+9×1.25%分接条件下换流变压器漏磁场的分布。

图5 漏磁场分布

可以看出，磁力线在绕组间主空道处分布较密，这是因为漏磁通所流经的路径大部分为非铁磁材料，磁阻近似为常数，因此漏磁通正比于产生它的电流大小。在绕组中部附近，磁力线大体呈现平行于绕组的轴向，此位置轴向漏磁很高。当接近绕组端部时，由于靠近上下铁轭及铁心等高导磁材料，根据磁力线沿磁阻最小路径闭合原理，漏磁通沿着方向相反的两个路径流通，从而引起较大的辐向漏磁。

3．3 磁场计算结果

短路电流最大时刻网、阀侧绕组轴向平均磁密分布如图6、图7所示。

图6 网侧绕组轴向平均磁密

图7 阀侧绕组轴向平均磁密

在绕组的上、下部，轴向平均磁密基本呈对称分布。由于绕组中部一些线饼的实际线圈匝数较多，故中部区域安匝较大，导致这些线饼的轴向磁密较大。在绕组端部，磁力线发生弯曲，产生横向漏磁，从而使轴向漏磁分量减小，所以绕组端部线饼的轴向磁密最小。

绕组匝绝缘采用耐热纸构成，从而网、阀侧段间油道设计成小尺寸，致使其调压绕组匝间没有油道，故轴向平均磁密的分布曲线比较光滑。

3．4 辐向短路力计算结果

图8、图9给出了短路电流最大时刻网、阀侧绕组辐向短路力分布。可见，绕组分别受到向内压缩、向外扩张的辐向力作用。分布规律是:网、阀侧绕组上下端部的线饼受力最小，最大值出现在绕组的中部，即第81、260号线饼，对应辐向力的瞬变曲线如图10所示。最大值出现在t=0.01 s时刻，分别为 -333.293、340.558 kN。

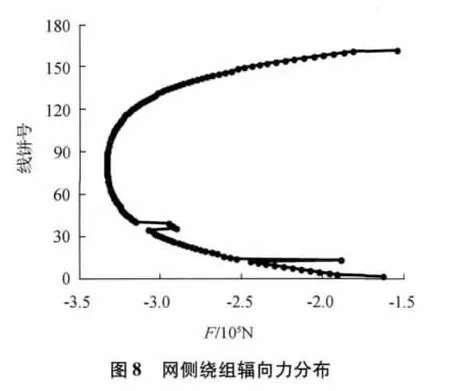
图10 辐向力随时间变化曲线

绕组上端所受辐向力比下端所受辐向力稍小，这是由于绕组上端距离上铁轭较下端距离下铁轭要远，使得上端部磁力线偏折现象更加明显而致。从图8可以看到，网侧绕组个别线饼的辐向力突然减小，主要因为这些线饼的线规和其它线饼的线规不同，匝数少于其周围线饼的匝数。

4 辐向稳定性校核

当线饼承受较大的辐向短路力时，可能造成网侧绕组压缩，使线饼弯曲或曲翘;阀侧绕组线饼伸长导致绝缘破损，进而引起绕组辐向失稳。故需校核线饼的辐向机械稳定性，其失稳平均临界应力可按式(6)计算[11]:

式中:FB为辐向失稳临界力，kN/m;E为铜的弹性模量，取1.225×105MPa;x为单根换位导线内导线的股数;y为与线饼和导线的结构有关的经验系数，取1.4;n为线饼内换位导线数;b、t分别为导线的辐向、轴向尺寸，m;m为绕组的有效支撑数，取实际撑条数的1/2;R为线饼平均半径，m。

分别对网侧绕组第81号线饼和阀侧绕组第260号线饼的失稳临界力进行核算，结果如表3所示。

表3 绕组线饼辐向稳定性计算结果

由式(6)计算得网、阀侧线饼发生辐向失稳的临界力分别为118.746、110.306 kN/m。线饼所受的最大辐向短路力均小于其强度的校核值，并具有足够的裕度，因此该换流变压器绕组具有足够的辐向机械强度。

5 结论

本文基于磁势平衡原理，在换流变压器阀侧绕组短路工况下，提出了一种利用有限元软件ANSYS计算绕组辐向短路电动力的方法。经算例计算分析表明，该方法建立的绕组2D“场-路耦合”模型是合理的，利用该模型能实现对漏磁场的分析及线饼辐向短路力的计算，且短路力最大值出现在t=0.01 s时刻。同时，对线饼辐向稳定性进行了校核，结果满足工程要求，这说明此方法可实现对换流变压器短路时绕组辐向机械强度的核算。

[1]赵鑫，吕培庚，况霞，等.特高压换流变压器的绝缘结构和试验[J].高压电器，2011，47(5):11-15.

[2]姜益民.变压器运行中短路损坏的常见部位及原因分析[J].变压器，2005，4(42):35.

[3]HYUNMO A，JIYEON L，JOONGKYOUNG K，et al.Finiteelement analysis of short-circuit electr-omagnetic force in power transformer[J].IEEE Trans.Power Electron，2011，47(3):1267-1272.

[4]王录亮，刘文里，高原，等.三绕组变压器低压绕组辐向短路力的计算方法[J].黑龙江电力，2011，33(6):421-425.

[5]焦立阳.电力变压器绕组短路电动力的计算[D].沈阳:沈阳工业大学，2009.

[6]韩晓东，翟亚东.高压直流输电用换流变压器[J].高压电器，2002，38(3):5-6.

[7]刘旸，陈庆国，魏新劳，等.换流变压器谐波损耗与瞬态漏磁场分析[J].黑龙江电力，2010，32(2):99-101.

[8]路长柏.电力变压器理论与计算[M].沈阳:辽宁科学技术出版社，2007:178-183.

[9]李晓松，胡贵，陈乔夫.基于“场-路耦合”分析的超导变压器绕组环流计算[J].电力电气，2006，25(10):21-24.

[10]阎照文.ANSYS工程电磁分析技术与实例讲解[M].北京:中国水利水电出版社，2006:12-26.

[11]谢毓城.电力变压器手册[M].北京:机械工业出版社，2003:173-179.