矢通量分裂法在喷管超声速喷流计算中的应用①

聂 赟，乐贵高，马大为

(南京理工大学机械工程学院，南京 210094)

0 引言

飞行器以Ma＞1速度飞行时，其发动机喷管尾部喷出的燃气流与超声速气流会产生强烈的相互干扰，形成间断及稀疏波系组成的复杂干扰流场［1］，这种气动干扰会直接作用于飞行器上，将影响其气动特性。因此，针对超声速射流问题开展相关研究是非常必要的。由于此类流动的风洞试验的复杂性及昂贵的费用，促使人们努力寻求经济性好、鲁棒性强及具有高精度的数值计算方法。国内外近年来发展了许多能够很好抑制伪振荡的数值格式，如 TVD、ENO和 WENO等［2－4］，均有很好的分辨率。20世纪 80 年代，Steger等［5］提出了矢通量分裂法，该方法是二阶精度、保单调的迎风格式，在空间离散时保持了迎风差分固有的耗散特性，能够避免过度的耗散。

在Steger等的基础上，本文将矢通量分裂法应用到轴对称Euler方程的数值求解，并对发动机喷管超声速射流问题进行了数值模拟。模拟结果与实验纹影图反映的流动特性基本吻合，与其他数值格式的计算结果相比较，发现该方法具有很好的间断捕捉能力。

1 矢通量分裂法

1.1 控制方程

轴对称无粘Euler方程组表示为

其中:

式中 Ω∈R2;T为时间变量;ρ为密度;u、v分别为x、y方向的速度分量;p为压强，对于理想气体满足状态方程p=(γ－1)pe;γ为比热容比;E为单位体积的总能量。

1.2 有限体积法和空间离散

在数值模拟中，对方程组(1)矢量形式的空间离散形式采用有限体积法。将计算空间离散为具有有限体积的小单元，并将计算得到的所需变量值存储在单元体的中心。

控制方程(1)采用矢量形式表示如下:

对流通量Fc为

Gc也可写成相似的形式。

为了离散流动控制方程:

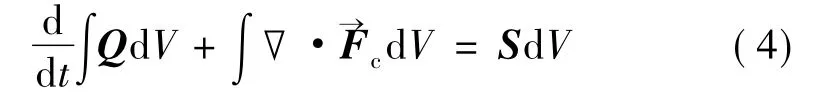
采用应用散度定理有

对于有离散体和区域组成的网格来说，方程(5)变化为

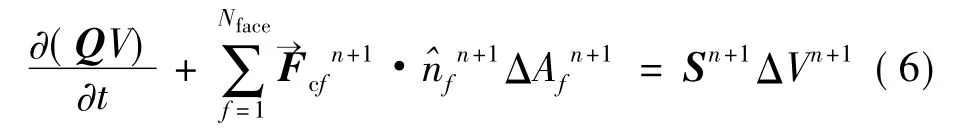
通过暂时略去某些下标给出线性化通量向量:

1.3 空间数值方法

矢通量分裂法基于Van-leer格式，矢通量分裂法对对流通量分裂为

定义表面法向马赫数Mn=(Vn＇)/c，其中Vn＇为垂直于单元表面的速度。

1≥Mn≥ －1 时:

式中 nx、ny为表面法向矢量。

通量向量线性化为

然后确定QL和QR，L和R是单元表面的左边和右边的外推变量值。通过外推原始变量值，然后构造左边和右边的守恒变量值。

1.4 多步Runge-Kutta时间离散

离散方程的求解通过时间步进法实现，采用多步Runge-Kutta方法数值求解方程组。在加入限制器的条件下，当采用矢通量分裂法进行空间离散时，数值解的精度在空间上可以达到2阶。因此，为了和空间上保持一致高阶精度，时间方向采用多步的Runge-Kutta方法。首先将时间［0，T］剖分为

对方程进行时间积分:

多步Runge-Kutta格式写成:

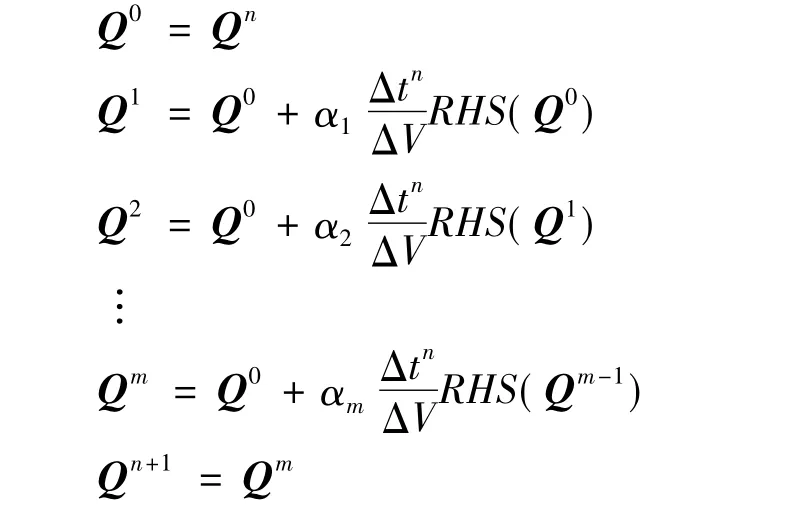
式中 α1为权重系数为时间步。

多步Runge-Kutta格式在m=1时为一阶时间精度，m≥2时为二阶时间精度。矢通量分裂法对时间步长有严格的稳定性限制条件，用多步Runge-Kutta显示时间步进格式进行时间离散时的时间步有CFL条件限制。

1.5 斜率限制器

在高阶情况下，为了提高方法的稳定性，在时间方向的迭代格式中引入局部斜率限制器，其思想是限制一阶斜率［6］，表达式为

计算时M取值参考文献［7］。

2 计算结果与分析

图1为发动机喷管喷流计算区域，取［0∶5］×［0∶1.5］，喷管尺寸与流动参数见表1，其中 l为喷管长度，r和R分别为喷管出口的内外径，下标j表示喷管出口的流动参数，下标∞为超声速外流的流动参数，计算区域内的网格数为6 000个。

图1 计算区域Fig.1 Calculation domain

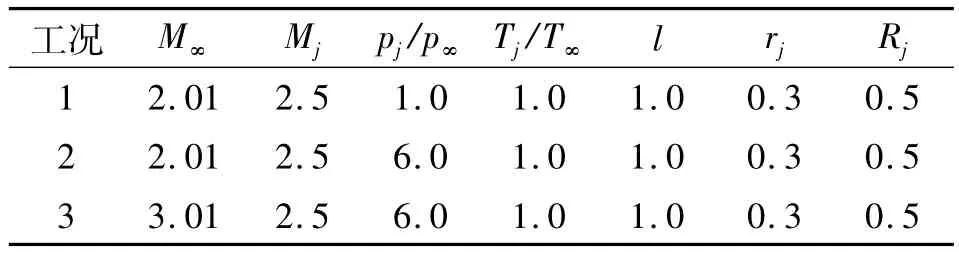
表1 流动参数Table 1 Parameter values of fluid flow

图2、图3分别给出了工况1、2的密度等值线图和马赫数等值线图及在相同流动条件下的试验纹影图。

从图2可见，超声速外流在喷管出口处开始压缩喷流，喷流近区马赫盘消失。形成两道间断的斜激波。第一道斜激波后面有膨胀扇，第二道斜激波后面是射流激波，射流膨胀区域受到外流动的压缩反射，反射激波与射流激波相交。计算结果与试验纹影图反映的流动特性很相似，能够较准确地反映发动机喷管喷流的流动特性。

从图3可看到，超声速外流与喷管喷流作用后，形成一道斜激波与射流激波组成的曲线激波，同样受到外流压缩，射流膨胀区域反射后形成反射激波。与工况1相比，反射点到喷管的距离明显增大，喷管出口处斜激波张角变大。在试验纹影图中得到了很好的验证。

图2 工况1的等值线和纹影图Fig.2 Contours and experimental schlieren picture of case 1

图3 工况2的等值线和纹影图Fig.3 Contours and experimental schlieren picture of case 2

图4是工况3的密度等值线图和马赫数等值线图。与工况2相比，变化的流动参数是超声速来流马赫数增大，射流的斜激波张角减小，激波反射点到喷管距离减小。

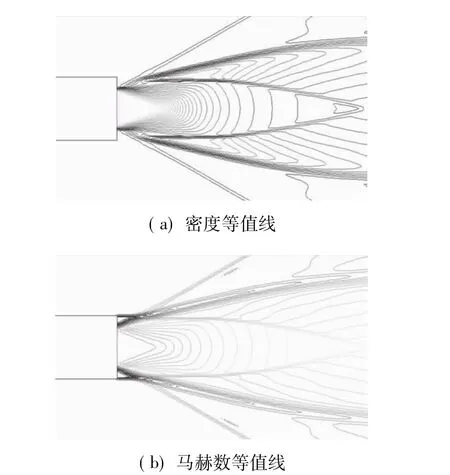
图4 工况3等值线分布Fig.4 Contours distribution of case 3

图5为工况1、2的喷管压强变化与实验结果比较曲线，p/p∞表示喷管壁面压强与自由来流压强之比。喷管壁面压强在出口处略微下降，数值结果与文献［8］吻合较好。

图5 壁面压强变化曲线Fig.5 Pressure distribution along wall

图6为工况2、3沿轴线的压强分布，压强变化趋势比较吻合。差异的造成主要是由于2种方法对间断点捕捉能力的不同。在激波发生反射后，反射点两侧物理量不连续。采用矢通量分裂法计算的压强曲线在反射点后有较大的压强梯度变化，而采用TVD格式在反射点计算的峰值被抹平，是由于该格式解的精度在该处降为一阶。因此，采用矢通量分裂法模拟超声速喷流是有效的，在反射点不会出现为振荡或抹平现象。

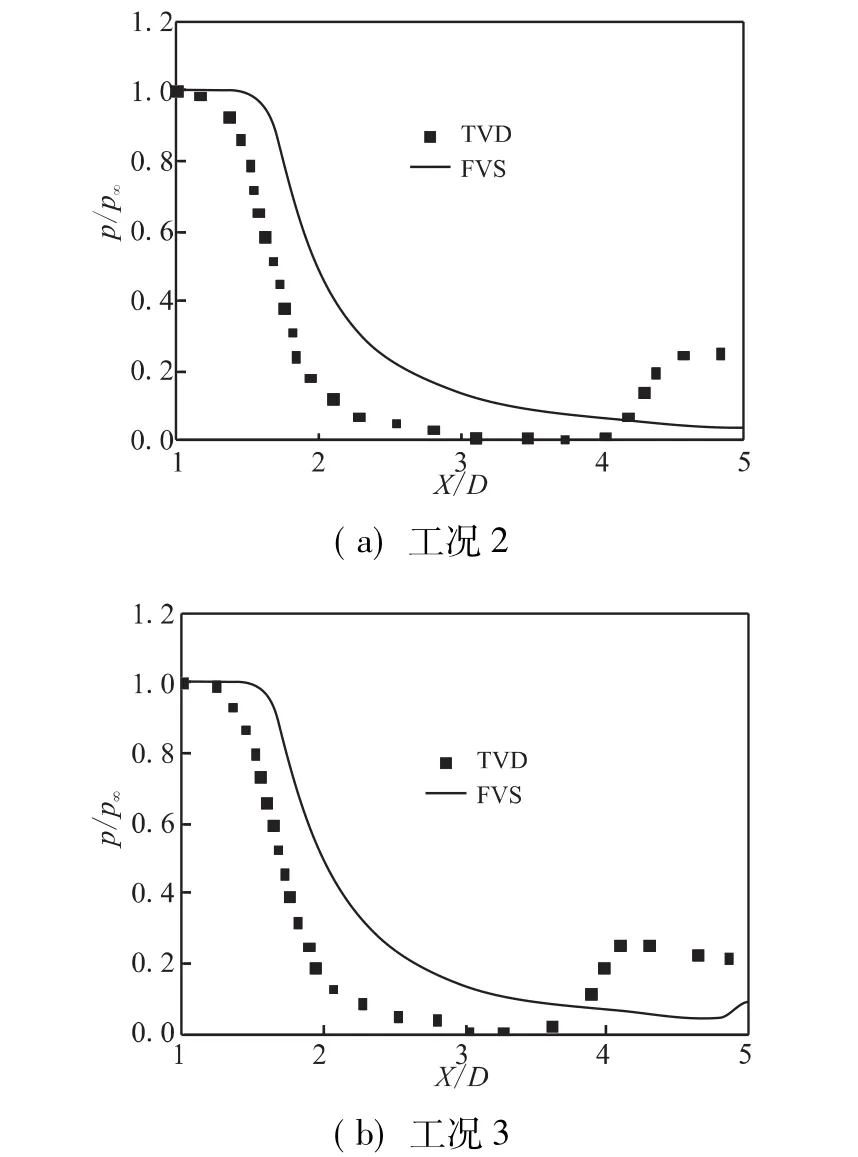
图6 轴线压强变化曲线Fig.6 Pressure distribution along jet axis

3 结论

(1)将二维矢通量分裂法应用到轴对称Euler方程的数值求解，并对发动机喷管超声速射流问题进行数值模拟，可实现对喷管超声速喷流问题的一个预测。

(2)用矢通量分裂迎风格式计算喷管超声速喷流流场是一条可实现的途径。利用矢通量分裂法对流动物理量和流场间断的高精度、高分辨率计算，能够促进喷管射流的应用和研究。

(3)利用本文的矢通量分裂法对流场间断的计算是成功的。能够有效的抑制间断附近的数值振荡，与其他格式的数值解相比，优于TVD格式。

(4)以二维轴对称喷管超声速喷流计算结果为基础，模拟结果与实验纹影图反映的流动特性基本吻合，与其他数值格式的结果相比，该方法能够较准确的捕捉到激波在轴线反射点的位置，且具有较高的分辨率，表明该方法在超声速喷流的数值计算中具有广泛的应用前景，有必要对其进一步的研究。

［1］瞿章华，刘伟.高超声速空气动力学［M］.长沙:国防科技大学出版社，2001.

［2］Liu X D，Osher S，Chan T.Weighted essentially non-oscillatory schemes［J］.J.Comp.Phys，1994，115(1):200-212.

［3］乔阳，刘勇，徐敏.基于多块对接网格的多侧喷流瞬态干扰特性研究［J］.固体火箭技术，2007，30(2):98-101.

［4］李立沛，徐敏.大攻角侧向喷流流场特性及喷流干扰效应［J］.固体火箭技术，2011，34(5):543-547.

［5］Steger J L，Warming R F.Flux vector splitting of the inviscid gas dynamic equation with application to finite difference methods［J］.J.Comp.Phys，1981，40:267-272.

［6］Cockburn B，Shu C W.The Runge-Kutta local projection P1-discontinuous Galerkin method for scalar conservation law［J］.M2AN，1991，337:337-361.

［7］Cockburn B，Shu C W.TVD Runge-Kutta discontinuous Galerkin method for conservation laws V:Multidimensional systems［J］.J.Comp.Phys，1998，144:199-244.

［8］Agrell J，White RA.An experimental investigation of supersonic axisymmetric flow over boattails containing a centered propulsive jet［C］.Sweden FFA Tech Note AU-913，1974.