内河航道挖槽立面二维水沙数学模型研究

吴 腾，吴玲莉，丁 飞

（河海大学港口海岸与近海工程学院，南京210098）

我国河流众多，水运资源十分丰富，但大部分河流含沙量较大，航道泥沙淤积严重，不得不消耗大量资金进行挖槽清淤以改善航道条件。由于航道挖槽改变了原有的河床形态，使水流流态更加复杂，同时也破坏了原有的水沙间的相对平衡，如何确定挖槽断面的尺寸，使挖槽后的泥沙回淤量较小就成为航道挖槽的关键问题。

关于减小航道淤积的研究由来以久，但由于航道疏浚问题的复杂性，且相关实测资料较少，使得该问题的研究难度较大。随着计算机技术的快速发展，许多学者也采用数学模型研究该问题［1］。黄永健结合沿水流方向的一维水流运动和垂向二维泥沙扩散方程求解断面平均流速和含沙量浓度分布，再进行水流穿越河槽的不平衡输沙计算，得到航道挖槽的回淤量［2］，由于在求解过程中采用了一维模型计算流速，难以反映挖槽后由于河床变形产生的环流对泥沙输移的影响，因此，在不平衡输沙计算中挟沙力的计算结果与理论存在一定差异；为了更好研究航道挖槽后泥沙的回淤情况，夏军强建立剖面二维水流泥沙数学模型，该模型采用流函数-涡量方程，可以较好克服N-S 方程中计算动水压强较难的问题［3］。对于挖槽立面二维水沙数学模型而言，自由面和河床形态是在不断变化的，随着计算时间的推移，模型的计算区域都可能随时间变化，如果保持网格不变化，在计算过程中难免带来误差，当误差大到一定程度就有可能导致程序的振荡与发散，对模型计算极为不利。因此，在模型中应充分考虑自由水面和河床变化问题。

水体产生的压强常简化为静水压强，在航道挖槽后，河床地形发生剧烈变化，水流流态也发生较大变化，对于立面二维模型，需要考虑动水压强与静水压强的差异。为此，本文拟采用有限体积法建立内河航道挖槽回淤立面二维水沙数学模型。该模型将采用动网格技术，使计算区域随流动区域的变化而改变，这将有效地减少网格与计算区域不重合带来的误差，更好地模拟自由表面和河床的变化；同时，模型计算中将引入静水压强修正值，克服因挖槽断面形态变化引起的流速剧烈变化带来的模拟困难。采用该模型探讨航道挖槽后泥沙回淤的机理，分析了不同挖槽断面形态与流态变化和泥沙淤积的关系，为挖槽尺寸的优化设计提供参考。

1 内河航道挖槽立面二维模型的建立

1.1 基本方程

航道挖槽后，槽内水沙运动可采用下列方程进行描述［4］。

水流连续方程

水流运动方程

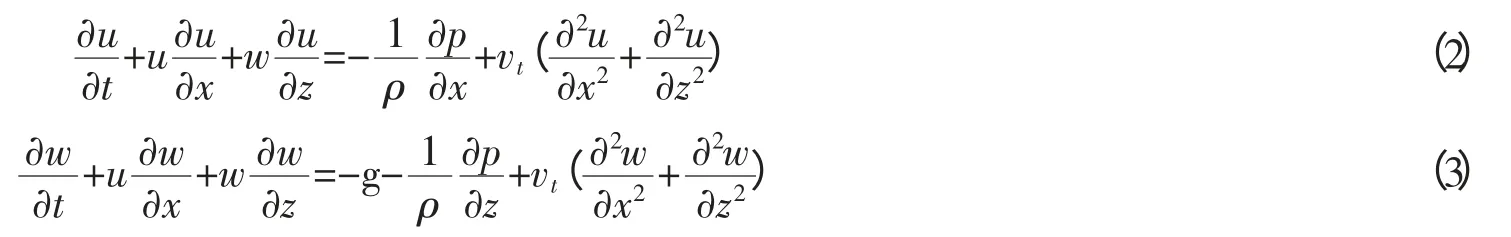
悬移质运动方程

河床变形方程

式中：u 为沿水流方向流速；w 为垂向流速，以向上方向为正；p 为动水压强；ρ 为清水密度；vt为紊流粘滞性系数；h 为水深；ε 为泥沙紊动扩散系数；Zb为河床高程；ω 为泥沙沉速；pr为计算参数；sa、s*a床面含沙量及挟沙力；γ′泥沙干容重。

1.2 考虑动水压强的水流方程

（1）动水压强的引入。

航道进行挖槽后，河道断面形态发生较大改变，水体的动水压强分布不能简化为静水压枪分布，为了使水位函数ξ（x，t）与动量方程密切联系起来，将动水压强分解为静水压强和一个压强修正值

式中：p′为压强修正值，是在水体流动时由于流线弯曲和流速不均匀所产生的附加压强；ps为静水压强，可表示为

式中：ξ 为水位；y 为河床高程；ρ 为清水密度；g 为重力加速度。

将压强分解后，压强梯度可分别改为

将式（9）代入水流运动方程式（2）和式（3），水流运动方程变为

（2）自由表面的处理。

式中：u 为x 方向沿水深平均流速；h 为水深；ξ 为水位；vs为水面流速。在程序编制中，可事先预留部分网格，判断是否过水来确定是否进入程序计算。

（3）方程统一形式。

综合上述修改，方程（1）、（10）、（11）、（4）、（5）和（12）即为本文建立的航道挖槽回淤立面二维水沙数学模型基本方程，连续方程和动量方程可写成统一形式

方程的离散采用有限体积法，离散形式可参考文献［5］。

表1 式（13）各参变量形式Tab.1 Parameters expression in formula（13）

2 相关问题的处理

（1）进口断面。

进口含沙量分布依据张瑞瑾、丁君松方法的含沙量垂向分布［6］

式中：s 为进口断面平均含沙量；ξ 为相对水深；I 为参数，根据丁君松的研究，I 与悬浮指标Z 的关系应为

（2）水面泥沙边界条件。

（3）河底泥沙边界条件。

式中：Sb*为近底挟沙力，文中采用van Rijn 提出的方法进行计算［7］。

（4）关于运动粘性系数vt的确定。

文中紊动粘滞性系数由下式确定［8］

式中：U*为摩阻流速；H 为断面平均水深；α 为常数，α=0.25～1.0。

3 模型的验证及分析

3.1 流速的验证

模型的验证采用文献［3］中的挖槽试验数据，试验的尺寸及水流条件为槽沟上下边坡坡度均为1:2，槽底宽为1 m，深度为0.2 m。进口处水深为0.2 m，垂线平均流速为0.4 m/s。同时假定在进口处于输沙平衡状态,即床面保持不冲不淤，相应的悬移质垂线平均含沙量为0.12 kg/m3，中值粒径为0.1 mm。计算网格为50×20个网格，网格长度分别为0.05 m 和0.025 m。图1 为0.4 m、1.1 m、2.2 m 处断面垂向流速验证。

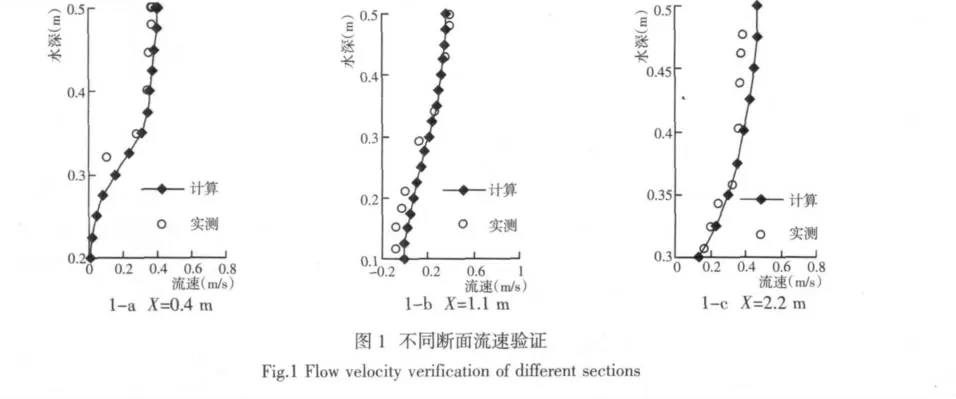
可以看出进口断面与出口断面流场较为平顺，在挖槽由于断面形态突变，流场较为复杂。定量上，模型的计算值与实测值较为接近，能反映挖槽断面的流速变化规律，可用于挖槽的研究。图2 为挖槽断面流场图，图3 为挖槽坡脚局部放大流场图，受挖槽断面形态影响，挖槽坡脚出现明显的回流。

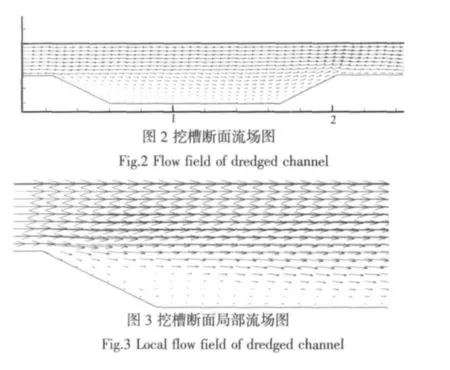
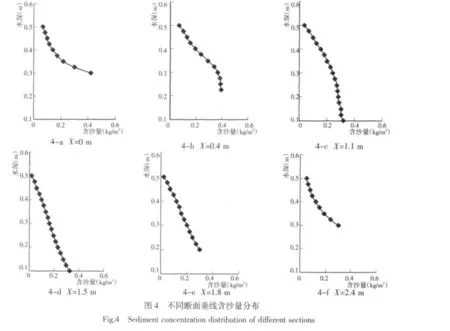
3.2 垂线含沙量计算分析

图4 为挖槽不同断面垂线含沙量分布，含沙量浓度分布上稀下浓，进口断面含沙量上下浓度差异较大，随着水深的增大，挖槽断面逐渐扩大，产生回流，断面上下浓度交换增多，断面的含沙量梯度减小，挖槽后的断面流速逐渐平顺，与河床发生交换，垂向浓度又稍有增大，与定性分析相同，说明该模型能计算含沙量的分布。

4 结论

本文将模型中的压强项分解为静水压强和修正压强项，建立了动水压强的立面二维水沙数学模型，同时该模型采用了动网格技术，使计算区域随流动区域的变化而改变。采用试验资料对该模型进行检验，结果表明，该模型能较好反应航道挖槽后流速、含沙量的变化，能清晰模拟由挖槽产生的横轴环流；此外，模型还能较好模拟航道挖槽后断面含沙量的垂向分布，可供挖槽后的回淤估算提供参考。

［1］Leedertes J J. A Water Quality Simulation Model for Well-Mixed Estuaries and Coastal Seas［M］. Santa Monica:Rand，1970.

［2］黄永健. 长江口挖槽自然回淤的计算［J］. 泥沙研究，1997（2）：69-73.HUANG Y J. Calculation of Natural siltation in Yangtze Delta excavation［J］.Sediment Research，1997（2）：69-73.

［3］夏军强，谈广鸣. 横向槽沟内泥沙淤积与水平轴环流变化的数值模拟［J］.水利学报，1998（8）:51-56.XIA J Q，TAN G M. Numerical Simulation of sediment deposition and horizontal axis circulation flow in lateral trenches［J］.Journal of hydraulic engineering，1998（8）:51-56.

［4］余明辉，吴腾，杨国录. 剖面二维水沙数学模型及其初步应用［J］.水力发电学报，2006，25（4）:66-69.YU M H，WU T，YANG G L.Study on vertical 2-D sediment numerical model and its primary application［J］.Journal of hydroelectric engineering，2006，25（4）:66-69.

［5］吴腾. 坝区水沙立面二维数学模型研究［D］. 武汉：武汉大学，2005.

［6］张瑞瑾. 河流泥沙动力学［M］.北京：中国水利电力出版社，1998.

［7］Van Rijn L C. Sediment transport，part Ⅱ：suspended load transport［J］. Journal of hydraulic Engineering，ASCE，1984，110（11）:1 613-1 641.

［8］韩其为. 黄河泥沙若干理论问题研究［M］.郑州：黄河水利出版社，2010.