简约而不简单——一道选择题揭秘与推广

☉江苏省南京金陵中学河西分校 李玉荣

简约而不简单
——一道选择题揭秘与推广

☉江苏省南京金陵中学河西分校 李玉荣

在《圆》的复习测试时，笔者选用了2010年湖北省武汉市的一道中考题：

如图1，⊙O的直径AB的长为10，弦AC长为6，∠ACB的平分线交⊙O于D，则CD长为（ ）.

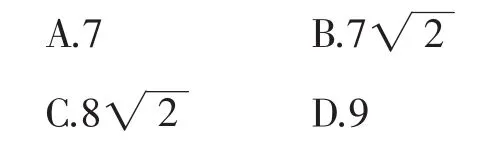
图1

此题设计简约、大方，但思维含量颇高，有一定的难度，测试的结果不尽如人意，鉴于这是一道选择题，学生有可能猜出答案，笔者特意做了考后调查，发现答案正确而真正会解的学生更是凤毛麟角，这引发了笔者的悉心思考.在讲评试卷时，笔者给出了几种解法，帮助学生揭开了这道选择题神秘的面纱，也开阔了学生的解题视野，极好地训练了学生的思维.

分析1：注意到∠ACD=45°、AC=6与CD在同一个三角形中，可先设法求出AD，再过点A作弦CD的垂线CH，构造直角三角形后利用勾股定理分别求出CH、DH的长从而求解.

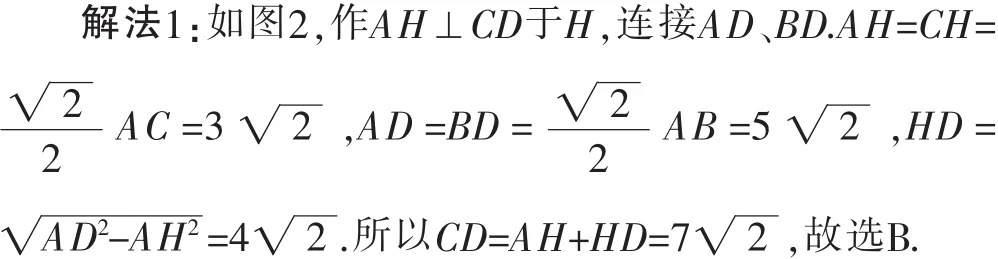
评注：过点B作BH⊥CD于H，可同样求解.

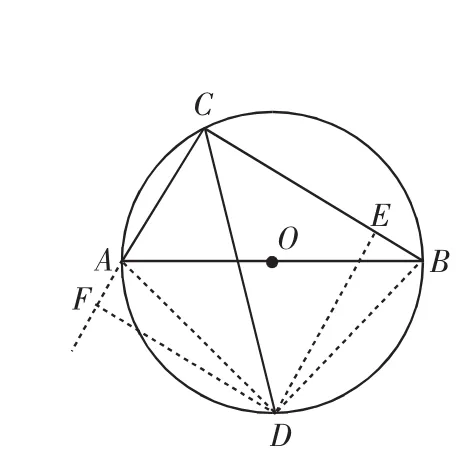
图3

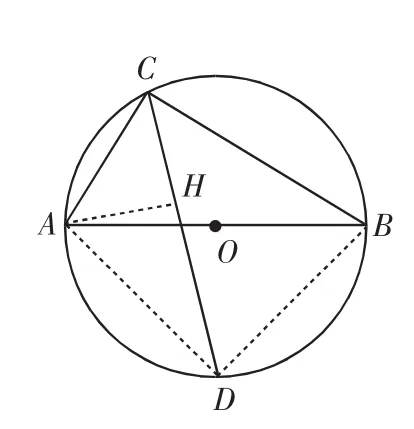
图2

分析2：注意到CD是角平分线，可考虑利用“角平分线上的点到角的两边的距离相等”这一性质添加辅助线求解.

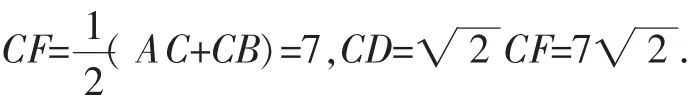
分析3：注意到CD是角平分线，可以CD为一边构造一个与△ACD全等的三角形求解.

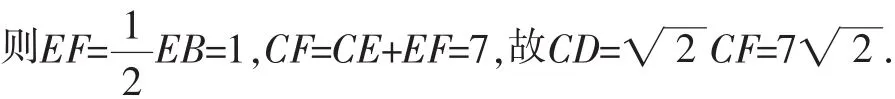
评注：在CA的延长线上截取CE=CB，可同样求解.

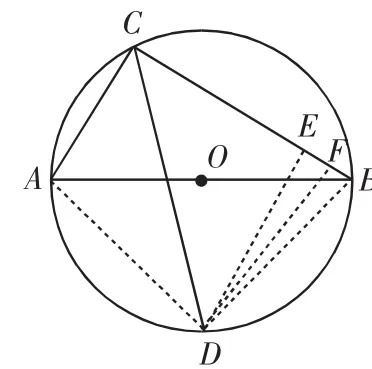
图4

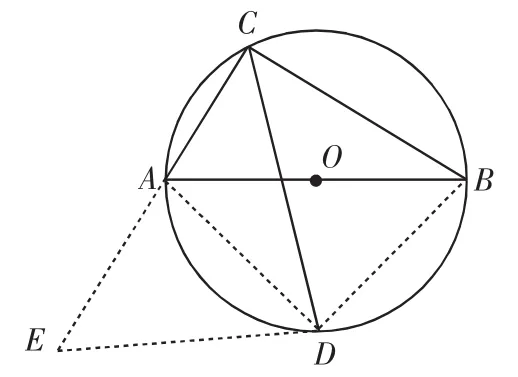
图5

分析4：以CD为直角边构造直角三角形直接求解.

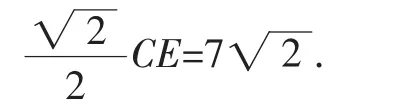
评注：过点D作DE⊥DC交CB的延长线于点E，可同样求解.

分析5：连接AD、BD，先求出四边形ADBC的面积，再利用面积关系求解.

解法5：如图6，连接AD、BD、OD，分别作AF⊥CD于F，BE⊥CD于E，∠AOD=2∠ACD=90°.

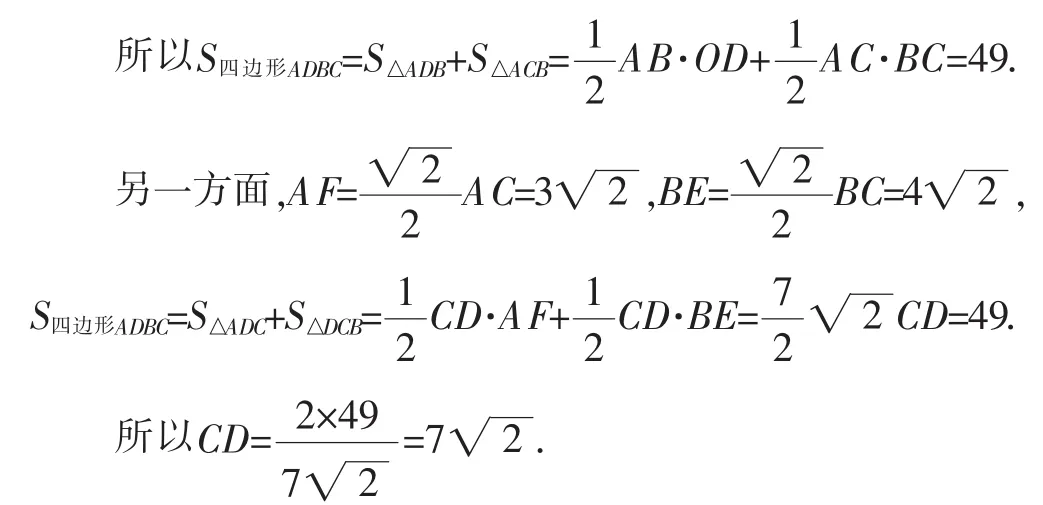
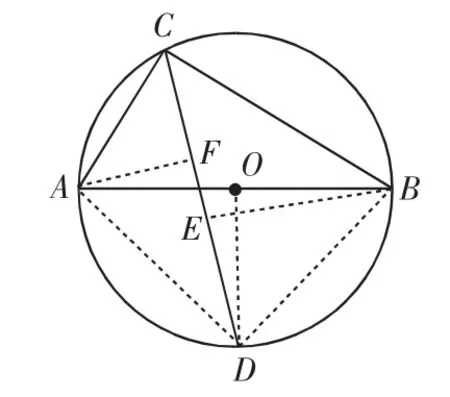
图6

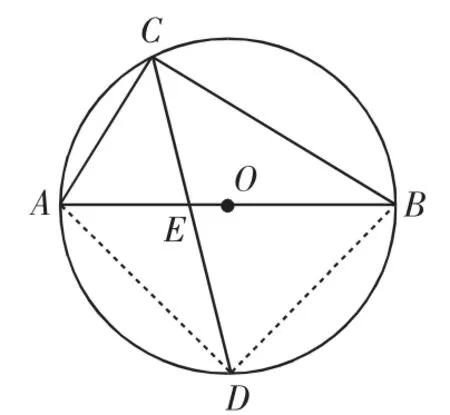
图7

分析6：设CD交AB于点E，有△ACE∽△DCB，△BCE∽△DCA，可分别列出含CD的比例式进而求解.

分析7：设CD交AB于点E，有△ACE∽△DCB，△BDE∽△CDB，可分别列出含CD的比例式进而求解.

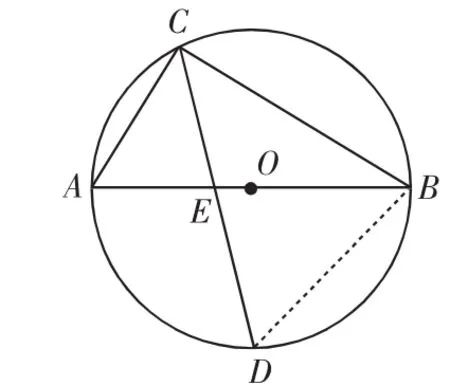
图8

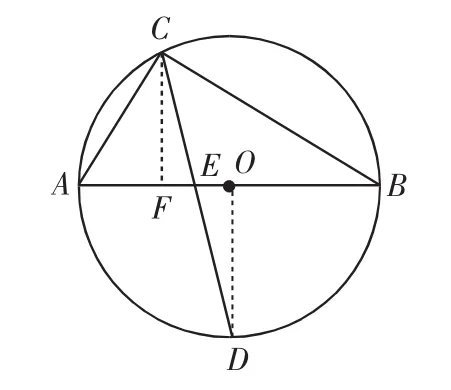
图9

分析8：设CD交AB于点E，构造直角三角形求出DE、CE，从而求解.

分析9：设CD交AB于点E，先构造直角三角形求出AE、CE，再利用相交弦定理求出DE后获解.

评注：作∠B的平分线交CD于点E，作EF⊥BC于点F，可同样求解.

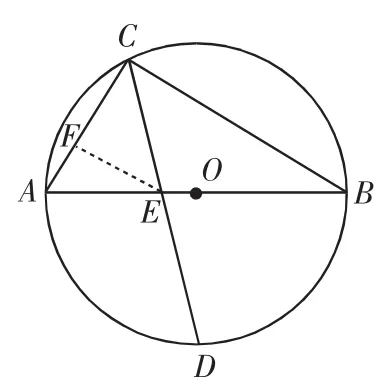
图10

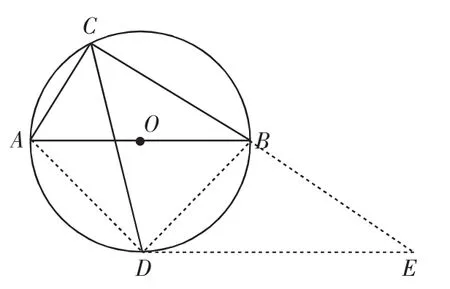
图11

分析10：过D作AB的平行线构造相似三角形，利用比例式求解.

解法10：如图11，连接AD、BD，过D作AB的平行线DE交CB的延长线于点E，则∠BDE=∠ABD=∠ACD=∠ECD，∠E=∠CBA=∠CDA.

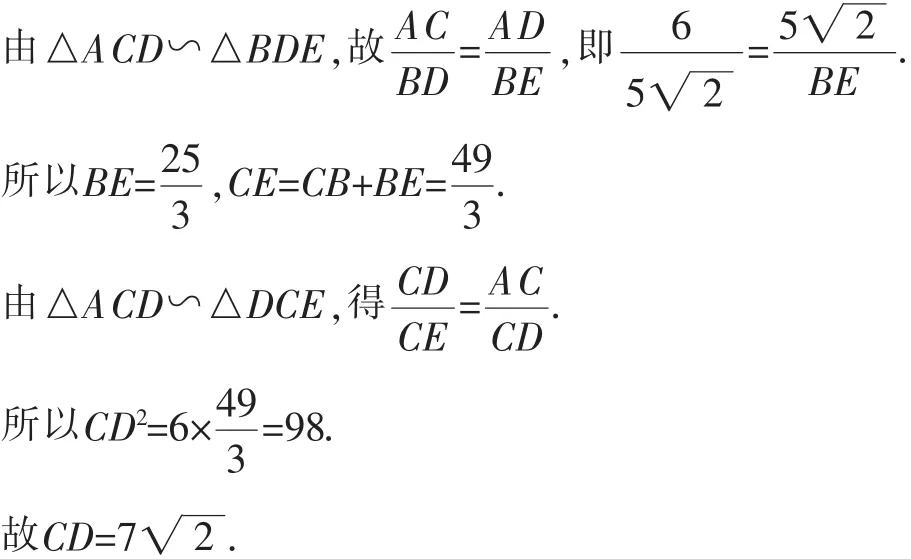
评注：过点D作AB的平行线DE交CA的延长线于点E，或者过点D作AB的平行线，可同样求解.

分析11：作直径CE，构造以CD为直角边的直角三角形可直接求解.

解法11：如图12，作直径CE，连接DE并延长与CB的延长线交于点F，连接BE，因为CE是直径，所以∠CDF=∠CBE=90°.

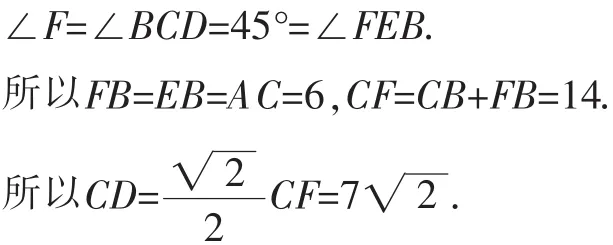
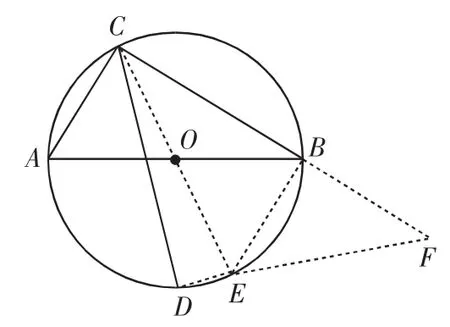
图12

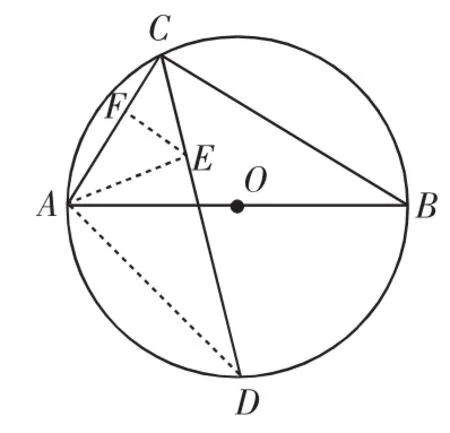
图13

分析12：注意到CD是角平分线，可再作一个角的平分线得到△ACB的内心E，分别求出CE、DE，从而解决问题.

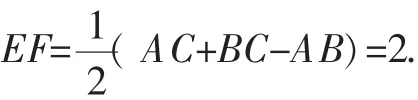
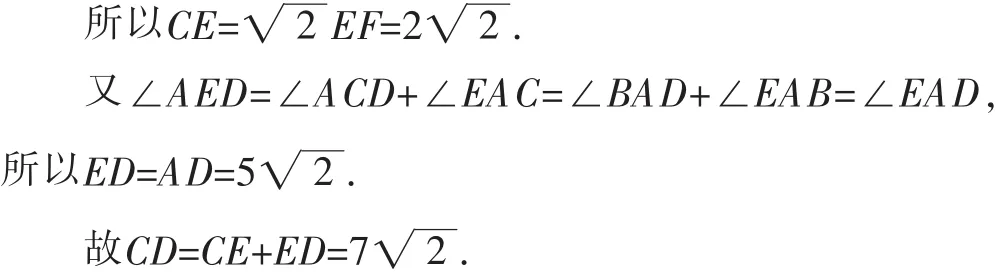
评注：作∠B的平分线交CD于点E，作EF⊥BC于点F，可同样求解.

分析13：注意到CD是弦，可作出弦心距，利用垂径定理、平行线等分线段定理求解.

解法13：如图14，作OG⊥DC于G，AE⊥DC于E，BF⊥DC于F.

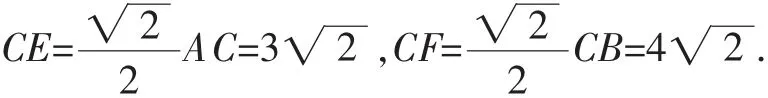
AE∥OG∥BF，OA=OB，根据平行线等分线段定理，得EG=FG.

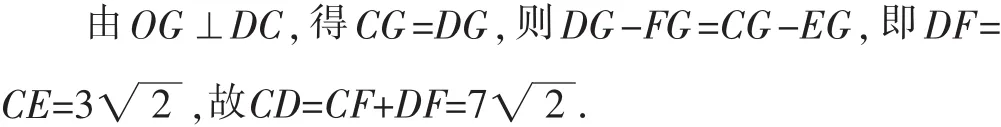
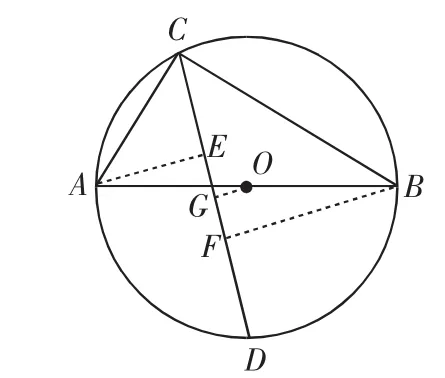
图14

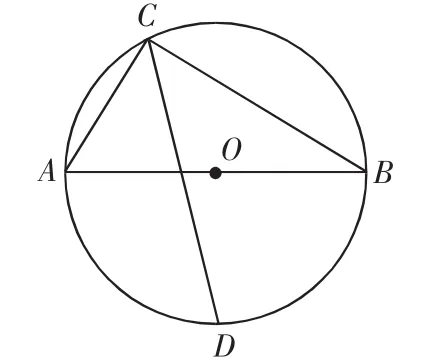
图15

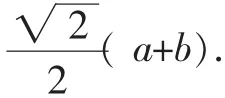
感悟：解决问题是数学的核心思维活动，解决问题后的反思是数学教学活动不可或缺的延续.本文探讨的这道选择题，虽然答案可依稀“猜出”，但反思其过程却有了上述意外的收获.可见，从解题过程合理性质疑到整体思路总结，从一种解法到解法的多样性，从原型到变式，通过这样有序的解题过程的反思，能不断丰富解决问题的方法和策略，形成解陌生问题的操作程序，理解数学解题思路分析中的“启发性”和“顿悟性”，并能运用这些方法寻找解题思路，从而提高解题效率，促进分析问题、解决问题能力的发展。