在中考题中渗透传统几何定理的命制策略
2013-02-01江苏省苏州工业园区青剑湖学校王春明
☉江苏省苏州工业园区青剑湖学校 王春明
在中考题中渗透传统几何定理的命制策略
☉江苏省苏州工业园区青剑湖学校 王春明
传统几何定理作为一种重要的数学资源,在中考题中有所体现.在由传统几何定理命制中考题时常用的策略有:方法借鉴、思路提炼、结论运用、问题拓展等.
一、方法借鉴
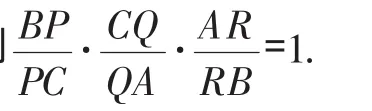
梅内劳斯定理是平面几何一个非常重要的定理,其证明涉及到相似三角形的判定与性质,但往往需要添加辅助线,常用的方法有:作平行线构造相似三角形,或作高利用面积法.由于平行线的添加有多种方法,使得定理的证明方法具有多样性.以该定理为背景命制中考题可以沿袭其证明方法的多样性,考查学生几何推理能力的灵活性和创造性;也可以将其改造成适合作为中考题的素材,然后适度整合.
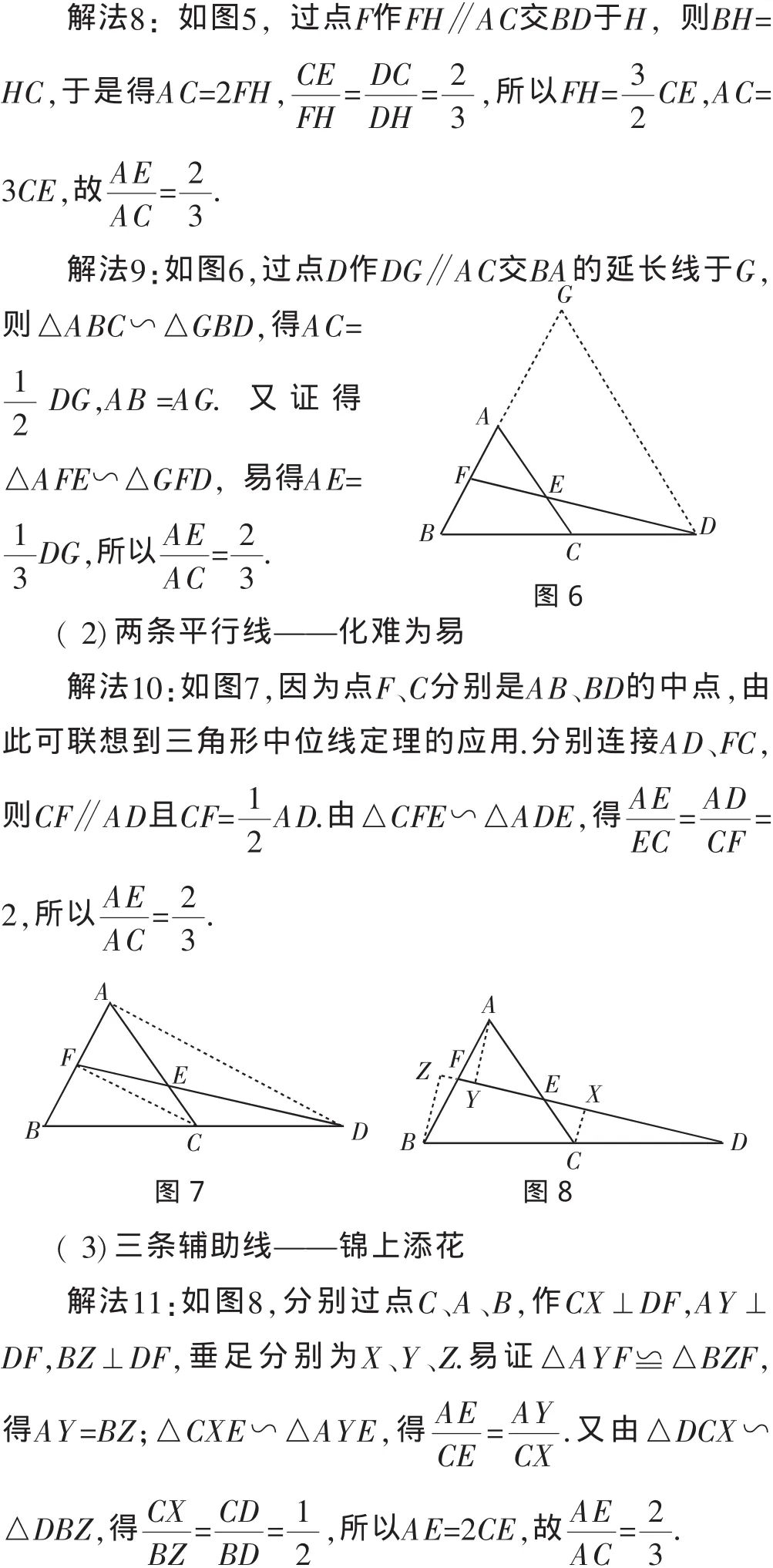
例1 (2009年潍坊市)如图1,已知△ABC,延长BC到D,使CD=BC,取AB的中点F,连接FD交AC于E.
( 1)求AE∶AC的值;
( 2)若AB=a,FB=EC,求AC的长.
说明:本题由梅内劳斯定理添加了两个特殊条件(AF=BF,CD=BC)得出的一道中考题,它也是一道传统的比例式典型题.试题给出的条件特殊,题型常规,解法多样,致使难度大大降低了.它主要是考查学生运用不同的数学思想、方法,从不同的角度思考、分析问题,以及探索出多种解题思路的能力,这对于开阔学生思维视野、培养和训练学生思维能力及教师今后的教学导向都具有极大的教育价值.
(1)一条平行线——五彩缤纷
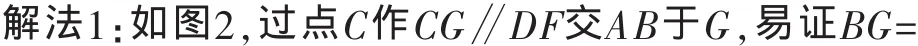
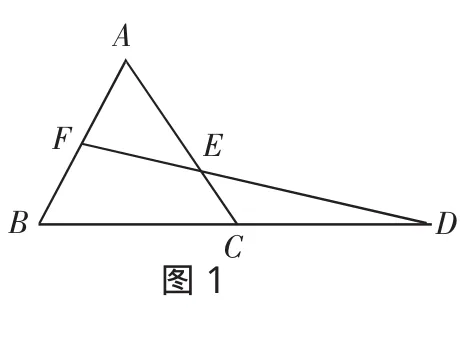
传统几何定理的证明方法中蕴含着丰富的思路、方法和数学文化.梅内劳斯(Menelaus)定理是指:若直线l不经过△ABC的顶点,并且与△ABC的三边BC,CA,AB或它们的延长线分别交于点P,Q,R,则
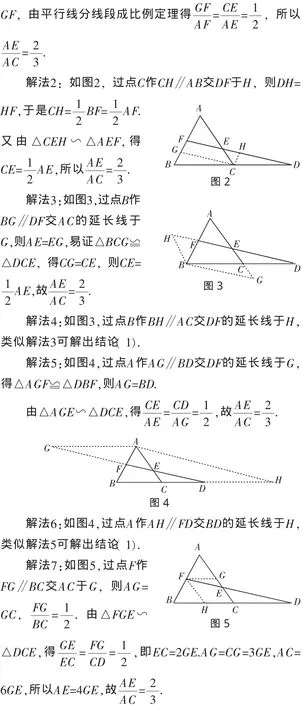
二、思路提炼
立足传统几何定理的思路,将典型的结论隐含在问题之中,通过恰当的方式予以呈现.
在一个三角形中,到三个顶点距离之和最小的点叫做这个三角形的费马点.为了便于改编为中考题,可以抽取费马点这样一个简单的性质:如果三角形的三个内角均小于120°,则在三角形内部对三边张角均为120°的点,是三角形的费马点.费马点性质证明思路的本质是通过旋转变换将三条线段转化到一条折线中,利用“两点之间线段最短”的公理,发现当且仅当∠APB=∠BPC=∠CPA=120°时三点共线,从而线段最短.几何变换作为课程标准新增加的内容,受到中考命题专家的重视,但如何渗透变换的思想,特别是旋转变换的思想方法,将基本的几何公理和实际问题(本题的实际模型是“将军饮马”问题)有机结合起来,学生感觉似曾相识,但又有所创新,这是一个很好的命题素材.

说明:本题由定义费马点入手,涉及的都是平面几何的核心知识,包括相似三角形的判定与性质、三角形全等的证明.其中的问题(1)不难解决,问题(2)要证明三条线段的和等于一条线段的长,基本的思路是截长法和补短法,如图10,可以在线段BB′上取点P,使∠BPC=120°,连接AP,再在PB′上截取PE=PC,连接CE.然后证明△ACP≌△B′CE,这里证明的思路是将△BPC绕点C旋转60°,这样可以得到∠APC=∠B′CE=120°,从而BB′过△ABC的费马点P,且BB′=PA+PB+PC.
该题属于不太难的试题,但能够触及费马点的本质,为了减小区分度设置了两个问题分别考查不同的知识点,起到有效调控的作用.
三、结论运用
一些经典的几何定理给人以美的享受,随着课程标准的日益普及,人们对传统的几何定理有所忽略,为了扭转这种局面,在中考题中适当利用传统几何题的结论改编一些中考题,可以弘扬传统文化,也能将传统几何定理和新课程理念进行对接.托勒密定理是初中学生完全能够接受的一个经典几何定理,所使用的知识都是一些基本的相似三角形的判定与性质,将其和全等三角形融合起来,可以采用“先获得结论,再予以证明”的命题思路,也可以构建“先探究结论,再进行推广”的命题策略.

四、问题拓展
著名的国际数学教育家波利亚说:“在数学的百花园中,生长着许多美丽的蘑菇,如果你有幸采撷到一朵,可千万别停步,看看它的周围,一定还生长着很多更美丽的蘑菇.”如维维安尼定理:等边三角形内一点到三角形三边距离之和为定值.这是等边三角形的一个性质,对其进行适当挖掘、发展,可以改编成中考题.
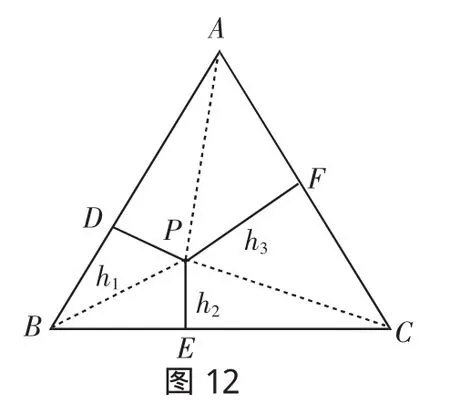
例4 如图12,已知点P是边长为a的等边△ABC内任意一点,点P到三边的距离PD、PE、PF的长分别记为h1、h2、h3、h1、h2、h3与a之间有什么关系呢?
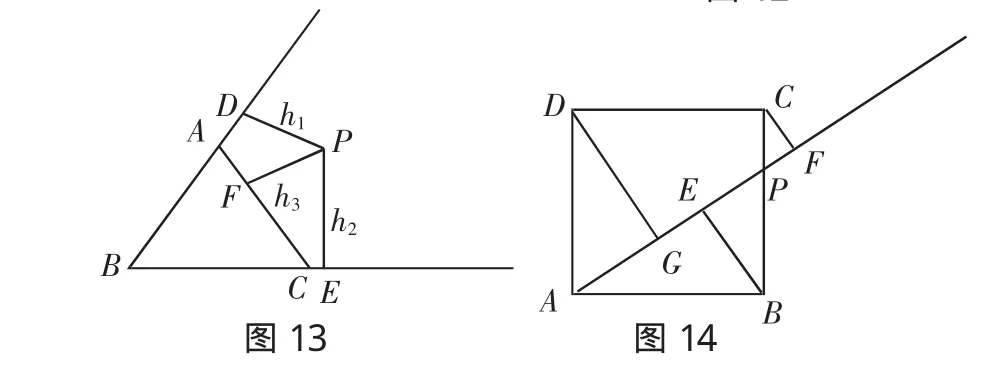

问题1:若点P是边长为a的等边△ABC外一点(如图13所示),点P到三边的距离PD、PE、PF的长分别记为h1、h2、h3.探索h1、h2、h3之间有什么关系呢?并证明你的结论.
问题2:如图14,正方形ABCD的边长为a,点P是BC边上任意一点( 可与B、C重合),B、C、D三点到射线AP的距离分别是h1、h2、h3,设h1+h2+h3=y,线段AP=x,求y与x的函数关系式,并求y的最大值与最小值.

