兼顾生产周期约束的模具制造系统双重资源优化配置方法

梁祖红，陈庆新，毛 宁，林佳瑜

（1.广东工业大学广东省计算机集成制造重点实验室，广东 广州 510090；2.广东工业大学图书馆，广东 广州 510090）

0 引言

模具是典型的面向资源的工程式订货生产模式。一方面，订单的交货期限制要求企业产品的平均生产周期不能太长，因此在制造系统的设计与规划阶段，就必须把平均产能和平均生产周期作为两项重要的指标看待；另一方面，社会发展使得我国劳动雇用成本逐渐上升，人力资源的数量和素质作为一项必须考虑的资源因素，在制造系统中的作用逐步增强，在模具企业中，设备与人力资源两个因素在订单成本中占了很大的比例。因此，本文在满足平均产能和产品平均生产周期约束的条件下，对模具企业中的设备与人力资源配置问题进行研究，具有重要的理论和工程意义。

有关资源配置问题的研究已有不少成果。Jacobsen等分析了人力资源在制造系统设计中的重要作用，据此建立了相应的模型，提出了制造系统设计准则，认为操作工的技能柔性尤其对所设计的制造系统柔性具有很大的作用［1］；Bitran等将制造系统最优设计问题分为目标化系统性能问题、最优化系统性能问题和设施划分问题三类，本文在考虑目标化系统问题的同时，也兼顾了产品的平均生产周期这一重要指标［2］；Pierreval等归纳总结了制造系统设计的相关问题，如单元组织、车间布局、资源配置优化和装配系统等，并对求解这些问题的演化算法分别进行了综述［3］；Ribeiro等建立了一个混合整数线性规划模型，同时优化能力受限资源的维护和在最大缓存容量的配置［4］；Can等针对基于仿真的制造系统建模的实验方法，提供了一种经验性的分析，这类方法可以将系统仿真结果利用经验公式表述出来，作为据此优化系统设计的约束条件［5］；Smith对制造系统设计与运作优化问题求解过程中的仿真方法进行了综述［6］；Bokhorst认为，在制造系统的范畴内，才刚开始考虑双重资源问题，截止到2003年，在该领域内只有有限数量研究报道，其中一个重要的特点是，操作工人需要培训多种技能，以具备操作多种机床设备的柔性［7］；Yue等进一步针对操作工人的技能柔性问题展开研究，认为操作工人的技能柔性包含多重因素，如多种技能及其所达到的水平、技能覆盖模式以及技能分布情况等，技能柔性的提高有助于扩展工作职责范围，操作工的技能柔性越高，制造系统需要的操作工人数就越少［8］；Hamedi等采用具有双重资源约束的多目标规划模型描述虚拟制造单元的设计问题，并采用Tabu Search算法近似求解［9］。随着模具企业生产系统设计所受的关注越来越多，我国学者对定制形式企业双重资源配置问题的研究更加深入。丁广太采用极大代数模型分析生产线上缓冲区大小与产能间的关系［10］；宋士刚根据生产线的特点，建立了一个简化的资源配置模型［11］。对双重资源约束（Dual Resource Constrained，DRC）制造系统的研究，国内仍集中在系统运作与调度方面［12－14］，还未见到有关DRC系统设计及资源规划的研究报告。

通过上述调研综述发现，目前关于模具生产车间生产能力规划的研究都是只单一考虑设备或者人力资源的约束，本文综合考虑了设备与人力资源双重约束下的资源规划问题；同时，双重资源配置研究的数学模型主要是混合整数规划和仿真模型，还未见到利用线性整数规划模型和仿真模型进行联合求解的相关研究。本文首先通过建立和求解松弛约束后的资源配置数学模型，获得仿真模型的设备与操作者初始配置参数，然后针对制造系统的典型特征进行仿真实验，从而获得设备与操作者的比例、各单元设备数量的合理取值范围等重要参数。接着根据制造系统的典型特征进行正交实验设计，并对仿真实验数据进行回归分析，得到约束条件的回归模型，将回归模型替代原有约束，获得原问题的近似线性整数规划数学模型，再用线性整数规划求得此近似模型的最优解，最后通过仿真实验结果检验方案的可行性。

1 模具制造系统双重资源配置问题

1.1 问题描述

根据实际生产情况可知，模具生产大都是单件，重复生产的概率很低，但针对零件的特征，可将生产的模具零件归为几类典型零件。假设模具生产车间主要生产N类零件P1，P2，…，PN；设备也按照所加工的零件分组划分为不同的单元，每一类零件都将通过独立单元加工，其中部分工件在独自完成若干道工序后，需要通过组装在一起进行加工（如型腔与电极组合后进行电火花加工）；各加工单元的设备和人力资源不能在单元间共享。考虑到订单的随机性，分别在前序加工单元的进口处和出口处设立缓冲区，而缓冲区的大小会限制系统的平均产能和产品的平均生产周期。由于这类企业的产品工艺技术含量高，生产现场的加工设备（很多是通用的高级数控设备）和劳动力（需要相当数量有经验的老师傅）成本相对较高，即这类车间受到双重资源的约束。因此，本文考虑的制造系统投资成本主要由设备和人力资源成本构成，在同时满足平均产能和平均生产周期约束的条件下，最小化制造系统的投资成本，即N类模具平均产能为α和产品平均生产周期为b时，设备数量与人力资源数量分别达到多少，才能使总投资成本最小。

针对上述问题描述，本文做出以下假定：规划期内产品的需求不存在随机性；设备与操作者不能在单元间共享；各类典型零件的工序单件标准工时定额确定已知；零件的工序单件标准准备工时与结束工时已知；某类加工设备每年工作的天数、每天提供的平均加工工时及采购成本已知；每位设备操作工人每年工作的天数、每天提供的平均工时及工资成本已知。

1.2 人与设备的双重资源规划数学模型

1.2.1 符号说明

使用到的符号有：

X为设备资源配置向量；

R为人力资源配置向量；

Y为缓冲区（buffer）配置向量；

η为调度策略向量；

P为投资成本。

1.2.2 问题的形式化描述

其中：式（1）为目标函数，即最小化投资成本；式（2）表示平均产能约束，实际平均产能Θ（X，R，Y，η）必须大于等于目标平均产能α；式（3）表示平均生产周期约束，实际平均生产周期Τ（X，R，Y，η）一定要小于等于目标平均生产周期b；式（4）明确提出设备和人提供的实际加工工时应该大于等于达到目标函数时所需求的设备和人的加工工时；式（5）表明X，R和Y为非负整数型向量。

1.2.3 存在问题

制造系统中的设备资源向量X、人力资源向量R、缓冲区向量Y和调度策略向量η同时决定系统的两项关键指标，即平均产能是否能达到α和平均生产周期是否小于等于b。要获得最小总投资成本P＊，需要同时找到最优的设备资源配置向量X＊、最优的人力资源向量R＊、最优的缓冲区配置向量Y＊和最优的调度策略向量η＊，使得平均产能约束Θ（X＊，R＊，Y＊，η＊）≥a 和平均生产周期约束Τ（X＊，R＊，Y＊，η＊）≤b同时成立。

根据利特定律［15］可知，随着生产系统中缓冲区的增加，平均产能也增加，但当缓冲区增加到一定程度后，不管它再增加多少，生产系统的平均产能都保持不变。因为缓冲区与平均产能间存在非线性函数关系，所以制造系统的平均产能和平均生产周期约束都无法用封闭形式表达，换言之，不能用函数形式描述设备、人力资源、缓冲区的大小、调度策略与平均产能和平均生产周期间的关系。这样一来，就不能用传统的非线性整数规划方法来求解制造系统双重资源优化配置问题。

1.2.4 求解思路

由于平均产能和平均生产周期这两个约束条件都无法用封闭形式描述，本文采用近似方法进行处理，用近似约束替代原有的无法用封闭形式表示的约束，构成近似优化问题。求解近似优化问题所得到的最优解，就是原问题的近似最优解。这里的近似方法是采用黑箱建模方法，即通过建立制造系统双重资源配置仿真平台，利用获得的部分仿真数据进行线性回归分析，用回归模型替代原有约束，从而获得原问题的近似线性整数规划数学模型。模具制造系统双重资源配置问题求解思路如图1所示。

2 双重资源优化配置近似求解

2.1 订单模型

在模具制造系统规划过程中，确定订单类型是很关键的一步。订单类型确定后，可以将订单的需求预测转化为对设备和人力资源总量的需求预测。因此，仿真平台一定要定义好订单模型，只有在确定制造系统中订单的类型与数量等后，仿真实验才能流畅运行和准确、有效地进行数据统计分析。同时，建立订单模型也使得仿真过程得到细化，让仿真实验平台更加贴近生产实际。

某模具生产企业的车间主要有A，B，C三类订单，每类订单都包含型腔、电极和镶件三类工件。其中A类订单包括1个型腔、64个电极（全部与型腔组合进行电火花加工（Electric Discharge Machining，EDM））和15个镶件；B类订单包括4个型腔、104个电极（全部与型腔组合进行EDM加工）和12个镶件；C类订单包括2个型腔、73个电极（38个与型腔组合，35个与镶件组合并进行EDM加工）和7个镶件。每类订单的型腔和电极都要经过计算机数字控 制 （Computer Numerical Control，CNC）和EDM两道加工工序，而针对不同类型订单的镶件就有不同的加工路线，A类订单的镶件只需要经过一道工序CNC，B类订单的镶件要经过CNC和线切割两道工序，C类订单的镶件要经过CNC、线切割和EDM三道工序。其中需要EDM工序加工的工件要与该工件相配合的电极协同加工。不同类型订单的工件在同一道工序的加工时间可能都不一样，其订单模型如表1所示。

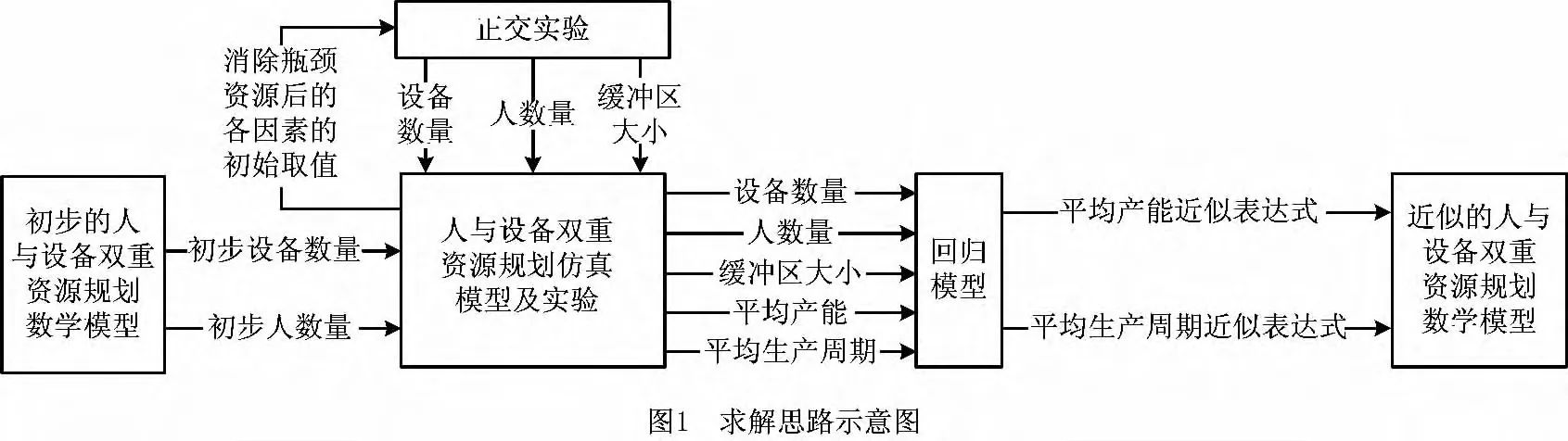
表1 订单模型

2.2 仿真模型建立与仿真实验

制造系统双重资源配置仿真平台搭建好后，只有确定了系统相关参数，才能在平台上进行大量的仿真实验，以获得资源优化配置所需的基础数据。在给定目标产能与平均生产周期的情况下，为了获得建立仿真模型所需设备和人力资源的数量，对原优化问题进行松弛，假设加工过程中，等待时间为0且设备利用率达到100%，在只考虑平均产能约束的情况下，给出松驰约束后的资源配置数学模型，通过求解数学模型可以得到建立仿真模型的初始参数，即设备和人力资源的数量。在此基础上，还针对模具制造系统的典型特征进行求解实验来获得相关系统参数，为后面的正交试验提供合理的仿真平台。

2.2.1 松驰约束后的资源配置数学模型

相关符号说明如下：

i为模具典型零件类型序号，i＝1，2，…，n；

j为单元序号，j＝1，2，…，p；

k为设备类型序号，k＝1，2，…，m；

l为第i类模具典型零件的工序序号，l＝1，2，…，ei；

ei为第i类模具典型零件的工序总数；

bi为第i类模具典型零件的总需求；

αijkl为第i类模具典型零件在第k类设备上加工第l道工序的标准工时；

βijkl为第i类模具典型零件在第k类设备上加工第l道工序的加工前准备工作时间；

γijkl为第i类模具典型零件在第k类设备上加工第l道工序的加工后结束工作时间；

h为每位工人每天能够提供的工时期量，1≤h≤8；

d为每位工人每年能够提供的平均加工天数，1≤d≤365；

η为每位工人一天的最高工作效率，0＜η≤0.8；

uk为第k类设备每天能够提供的平均工时期量，0≤uk≤24；

vk为第k类设备每年能够提供的平均加工天数，1≤vk≤365；

gkj为第j单元的第k类设备现有的数量，gkj∈N；

ck为第k类设备的单台采购价格，ck＞0；

δ为每位工人的工资成本，δ＞0；

xkj为第j单元需要增添的第k类设备的数量，xkj∈N；sj为第j单元装夹工作所需的工人数量，sj∈N；

rj为第j单元拆卸工作所需的工人数量，rj∈N；

μijkl为在第j单元第k类设备上加工第i类模具典型零件第l道工序的数量，μijkl∈N。数学模型描述：

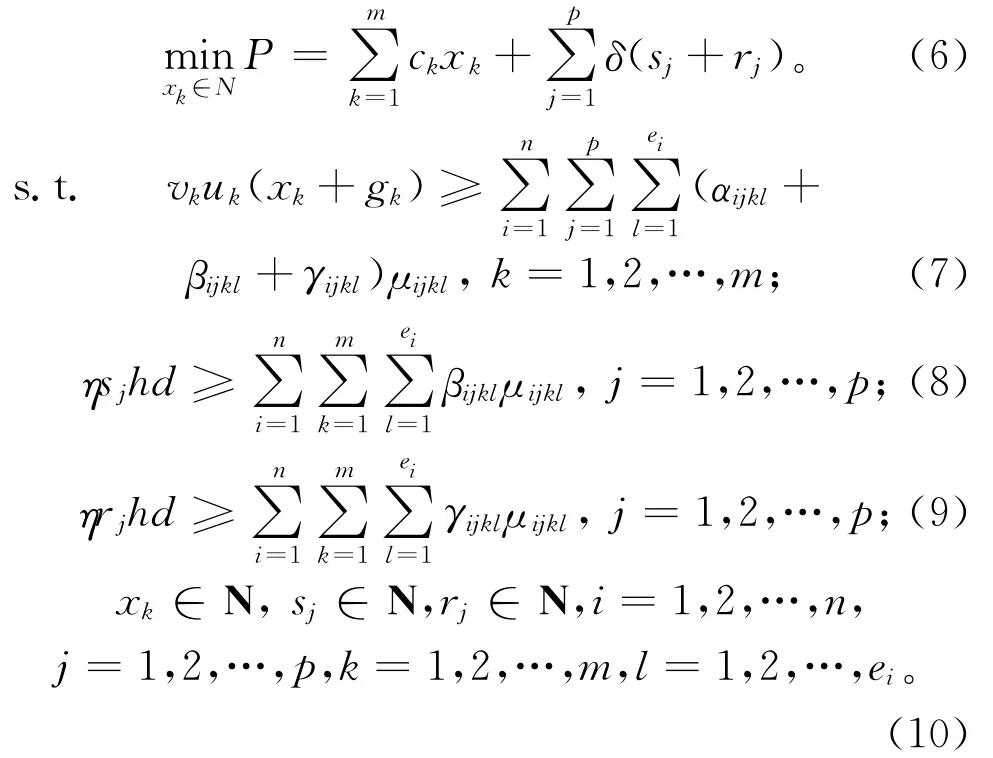
其中：式（6）为目标函数，即优化目标是使得下一个年度企业需要采购设备的总成本最低；式（7）表示需求与资源能力必须相适应，即对第i类模具零件提供的第k类加工设备的年度总供给（单位h），应保证市场提供的总需求（单位h）（每类设备能够提供的总工时必须满足各类零件对这类设备的总体加工工时的需求，这样的约束不等式共有m个）；式（8）与式（9）描述了工人能提供的工时必须要满足实际的劳动力工时需求；式（10）表示三个决策变量均为整数。

2.2.2 求解基于目标产能的仿真模型初始参数

上文提及的模具制造企业2012年～2015年的订单预测情况如表2所示；单元加工设备集的相关参数如表3所示；典型工件加工工艺与装夹、拆卸所需的劳动力工时如表1所示。每位工人能提供的工作天数平均为300d，每天能提供的工作小时数为8 h，工作效率为0.8；每位工人的平均工资成本为0.4万元／月。使用Lingo 11求解模型所得的结果如表4所示。

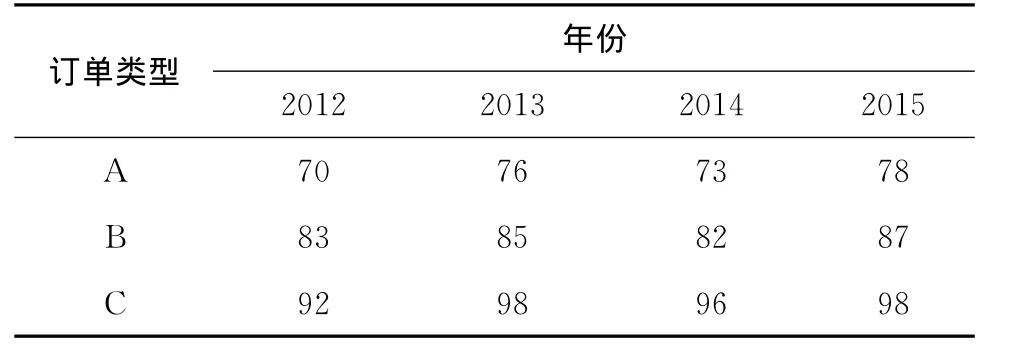
表2 生产订单预测情况

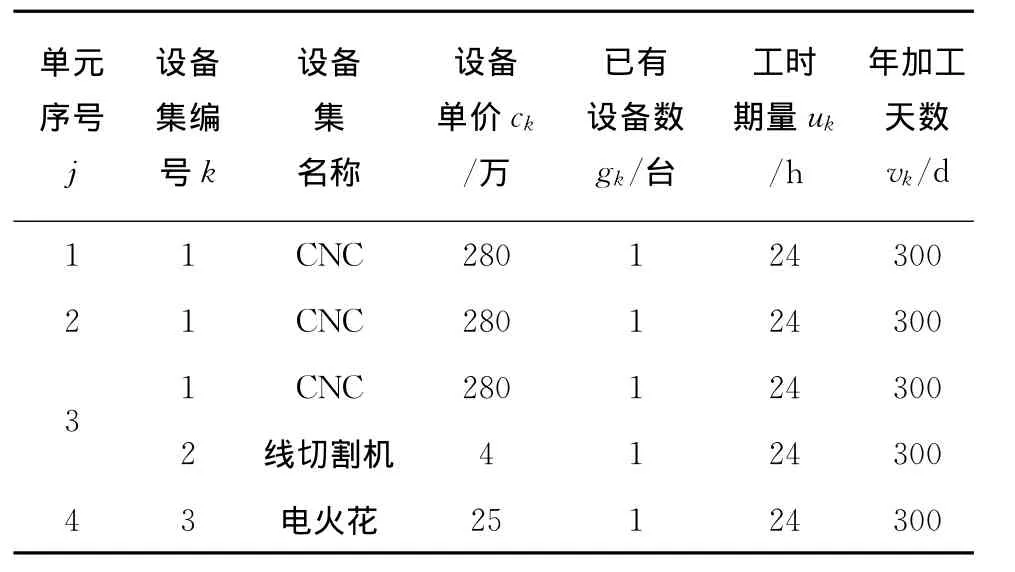
表3 单元设备集相关参数

基于松驰约束后的资源配置数学模型求解结果，根据实现2012年目标产能所需的设备和人力资源数量，本文运用先进的建模和仿真工具eMPlant，结合这类车间的实际运行情况，并应用面向对象的方法，建立如图2所示的人与设备的双重资源规划仿真模型。仿真模型分为订单产生、型腔CNC、电极CNC、镶件CNC、线切割、电火花加工六大部分，订单产生的规则是各类订单分别按300／订单的年总数这一频率产生。同时，仿真模型中的典型工件加工工艺、单元设备集相关参数、装夹与拆卸所需劳动力工时等参数都与数学模型的相关参数一一对应。在无法得到最优调度策略的情况下，该仿真模型采用先到先加工的策略，这也是制造企业使用最多的策略之一。

表4 人与设备的双重资源规划结果

2.3 仿真实验

从问题求解思路可以看出，制造系统双重资源配置仿真平台是制造系统双重资源优化配置问题的求解基础，因此仿真平台要能反映模具制造系统的典型特征。首先针对制造系统的典型特征进行仿真实验，获得各单元的设备数量合理取值、设备数量与操作工数量比例等系统相关参数，然后进行正交试验设计和仿真实验，获得仿真实验数据。

2.3.1 求解实验

制造系统的瓶颈控制着整个系统的运作，瓶颈的损失意味着整个生产系统的损失，瓶颈上的产出率决定了整个系统的产出率，因此如果瓶颈的制造系统配置不是最优的，那么增加非瓶颈资源不但不能提高系统产能，反而会导致系统总投资成本增加。只有各类设备的负荷达到均衡并达到较高的利用率时，才能实现制造系统的总投资成本最小并达到目标产能［16］。本文的求解实验一用前面建立的仿真模型进行仿真实验，再分析各单元的平均设备利用率和平均人力资源利用率，最后改变平均设备利用率较高的单元设备数量，得到实验方案并进行仿真实验，根据各单元的平均设备利用率确定各类设备数量比较合理的取值范围。通过仿真实验以及对实验结果的分析可以得出结论：当加工设备型腔CNC、电极CNC、镶件CNC、线切割、EDM的数量分别为5，6，11，2，7时，制造系统的设备负荷达到比较均衡的状态。同样，在后面的正交试验设计中，各单元设备数量的合理取值范围可参照求解实验的实验结果。

在模具制造系统中，当一个工件到达空闲的设备前，首先需要申请操作工安装，只有该申请获得满足才可以进行加工，如果申请不满足则工件必须等待操作工，而此加工设备也不能再接受其他新工件。工件的拆卸过程也存在同样的问题。因此，操作工数量与设备数量的比例一定要合理，否则会导致设备申请操作工人得不到满足，造成等待；或者由于操作工人数过多，造成人力资源的浪费。本文的求解实验二首先确定设备数量和缓冲区大小，再减少制造系统其中一个单元的操作工人数量，最后根据实验结果绘制装夹工人数量与各单元设备利用率的关系曲线。通过实验结果分析，根据式（13）和式（14）可以得到合理的设备与操作工数量比例。

在第j单元中，当一位装夹工人在一台设备上完成装夹工作后，这位工人还有时间αijkl到其他设备上进行装夹工作。因此，在第j单元，一位装夹工人最多能同时照看的设备台数为

同理，在第j单元，一位拆卸工人最多能同时照看的设备台数为

在得到第j单元中一位装夹或拆卸工人最多能同时照看设备的台数后，就可以获得如下设备数量与操作工人数量间的关系式：

（1）第j单元的装夹工人数量sj与设备数量xj间的关系式：

（2）第j单元的拆卸工人数量rj与设备数量xj间的关系式：

2.3.2 基于正交试验设计的仿真实验

建立制造系统双重资源优化配置仿真实验平台后，通过仿真实验可以获得平均产能和平均生产周期的具体数值。仿真实验虽然能得到精确的指标值，但是非常耗时，因此本文采用正交试验设计，争取做比较少的实验就可以获得比较全面的实验数据。正交实验设计法是使用已经造好了的表格（正交表）来安排实验，它能在很多实验中选出代表性强的少数实验条件，并能由此推断找到最好的工艺条件。正交实验设计在发达国家的农业实验、工艺流程设计中的应用很广泛，在我国也有很多成功应用的例子［17］。因此，本文利用正交实验法确定决定制造系统的平均产能和产品平均生产周期的向量取值，以争取通过较少的实验得到较全面的实验数据。

由上述问题描述可知，模具制造系统的平均产能和产品平均生产周期主要取决于加工单元的设备数量、设备操作人员数量、加工单元前的缓冲区大小和车间调度策略。本文的车间调度策略采用先进先出的方法，因此在正交实验设计中不考虑调度策略。由前面的求解实验可知，双重资源约束的制造系统中每个加工单元分别从事加工前准备工作与加工后结束工作的员工数量都可通过该单元的设备数量计算得到，因此在正交试验设计时只考虑设备因素。型腔CNC加工、电极CNC加工、镶件精加工三个单元前的缓冲区对系统的产能和生产周期也起很大作用，但考虑到订单所含型腔、电极、镶件的数量服从一定的比例关系，在试验设计时只考虑型腔CNC加工单元的缓冲区大小，电极CNC加工和镶件精加工前的缓冲区大小可根据型腔CNC加工单元的缓冲区大小计算得到。综合上述分析，本文的正交实验设计考虑的因素有加工设备型腔CNC、电极CNC、镶件CNC、线切割、EDM的数量，以及型腔CNC加工单元前的缓冲区大小。

现以实现2012年目标产能的设备与人员配置情况进行正交试验设计，根据求解实验的结果可知，当各单元设备数量的取值为5，6，11，2，7时，设备负荷比较均衡，没有明显的瓶颈现象，因此本文的正交试验设计分两步进行：①根据型腔CNC的数量与型腔CNC加工单元前的缓冲区大小生成正交表A，各因素的水平取值如表5所示；②选择表A中的每一行，根据相应型腔CNC的数量计算得到电极CNC、镶件CNC、线切割、EDM的数量，再由设备的数量与缓冲区的大小生成正交表B，各因素水平的取值如表6所示。

表5 正交表A因素取值说明

表6 正交表B因素取值说明

首先根据表5和表6的因素取值，并使用最常用的统计软件之一 ——SPSS17生成正交表共180行，即要做实验的次数为180。表7所示为正交表的一部分。

表7 正交表

根据正交试验表7，分别做如下180次仿真实验，表8所示为仿真实验部分结果。

表8 仿真实验结果

2.4 人与设备的双重资源近似线性整数规划数学

模型

（1）相关符号说明

Y为型腔CNC单元前缓冲区大小；

T为平均生产周期；

Pj为第j单元设备提供的实际工时，Pj＝vkuk（xkj＋gkj）。

其中：式（15）明确系统的最小产能为 ；式（16）显示系统的最大生产周期为T；式（17）表明第j单元的设备实际工时Pj与需求工时Rj相差小于1－φ，否则第j单元的设备会成为很明显的瓶颈资源。

3 基于回归统计的双重资源优化配置近似求解

通过在制造系统双重资源配置仿真平台上进行仿真实验，获得大量的仿真实验数据。首先对仿真实验数据进行逐步回归分析，得到平均产能和平均生产周期这两个回归模型；再用回归模型替代原有无法用封闭形式表示的约束，从而建立制造系统双重资源近似优化配置问题的数学模型；最后，利用线性整数规划，求解基于回归统计的制造系统双重资源近似优化配置问题。

通过对仿真实验数据进行回归分析，得到平均产能与平均生产周期的回归方程

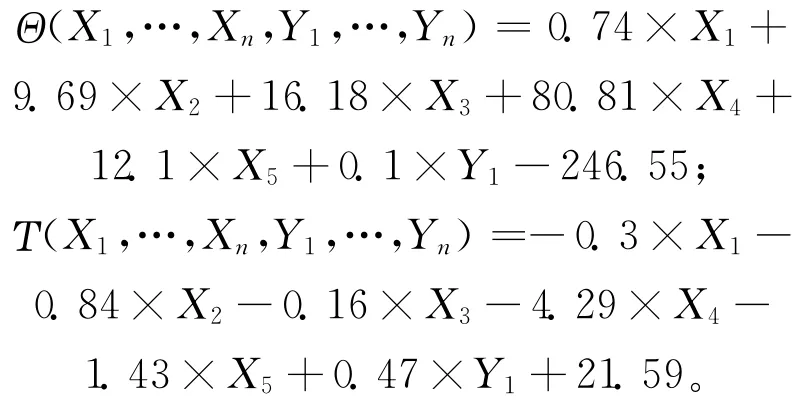
在得到平均产能和平均生产周期的封闭表达形式，即关于平均产能与平均生产周期的回归方程后，近似地替代优化模型中的原有约束，从而得到近似优化问题。现设定系统的最大产能为245，A，B，C三类订单的数量按表2中2012年对应的数值，同时产品的平均生产周期为11d。用Lingo 11求解近似数学模型，求解结果如表9所示。

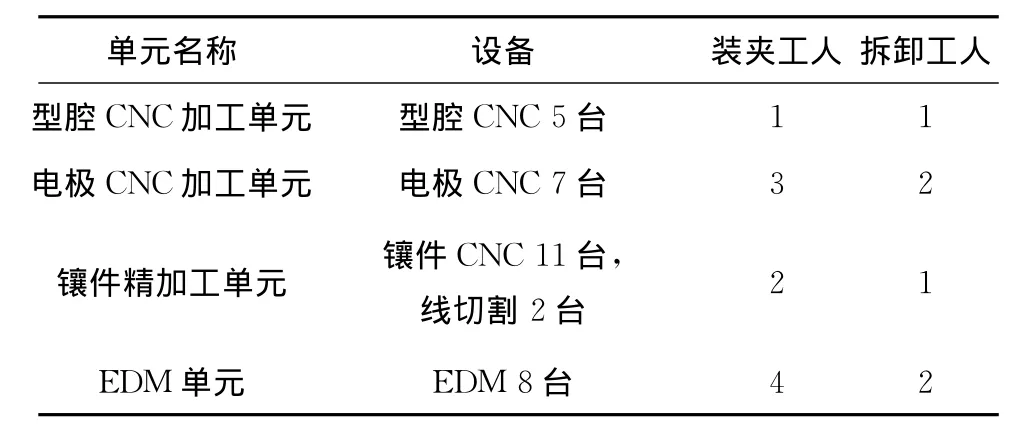
表9 近似数学模型求解结果

在获得数学模型的求解结果后，必须以仿真结果来验证人与设备的双重资源规划模型求解结果是否合理。首先按表9所列的数值配置人与设备双重资源规划仿真系统，然后开始仿真实验。在仿真系统运行600d、生产系统达到稳定状态时，600～900这300d的产能为245，产品的平均生产周期为6.9 d，人与设备的利用率如图3所示。

从图3可以看出，各单元的设备利用率相差不大，没有出现瓶颈资源。同时人的利用率最高是77%，小于前文设定的工人的最高工作效率，同时仿真系统的平均产能和产品的平均生产周期都满足规划时设定的约束。因此，仿真实验的结果很好地证明了改进的数学模型所得的结果是合理的，从而也说明把优化问题转换为近似优化问题这种近似求解方法是可行的。

4 结束语

本文针对模具制造系统的显著特点，建立了制造系统双重资源优化配置的数学模型，因为系统的平均产能和平均生产周期这两个约束条件无法用封闭形式表示，所以不能采用传统的非线性整数规划模型求解。本研究把原问题转化为近似优化问题，通过求解近似优化配置问题的最优解，获得原问题的近似最优解，即通过建立制造系统双重资源配置仿真平台，利用获得的部分仿真数据进行线性回归分析，分别得到平均产能和平均生产周期的回归方程；用两个回归方程分别替换原问题中不能用封闭形式描述的平均产能和平均生产周期这两个约束，从而建立制造系统双重资源近似优化配置数学模型；利用线性整数规划方程对数学模型进行求解，获得设备和人力资源的数量，通过仿真实验检验，证明得到的解是可行的。仿真实验的结果很好地验证了求解基于回归统计的制造系统双重资源近似优化配置数学模型所得的双重资源配置方案的可行性，进而表明把优化问题转换为近似优化问题的近似求解思路的可行性。

下一步工作是，对近似问题和近似解的近似程度进行分析和评价，使模具生产车间设备与人的双重资源规划结果更加精确。

［1］ JACOBSEN P，PEDERSEN 段 ，JENSEN J N，et al.Philosophy regarding the design of production systems［J］.Journal of Manufacturing Systems，2001，20（6）：405－415.

［2］ BITRAN 段 ，MORABITO R.An overview of trade－off curves in manufacturing system design［J］.Production and Operations Management，1999，8（1）：56－75.

［3］ PIERREVAL H，CAUX C，PARIS 段 ，et al.Evolutionary approaches to the design and organization of manufacturing systems［J］.Computers ＆ Industrial Engineering，2003，44（3）：339－364.

［4］ RIBEIRO 段 ，SILVEIRA S L，QASSIM Q S.Joint optimization of maintenance and buffer size in a manufacturing system［J］.European Journal of Operational Research，2007，176（1）：405－413.

［5］ CAN B，HEAVEY C.Comparison of experimental designs for simulation－based symbolic regression of manufacturing systems［J］.Computers ＆Industrial Engineering，2011，61（3）：447－462.

［6］ SMITH 段 .Survey on the use of simulation for manufacturing system design and operation［J］.Journal of Manufacturing Systems，2003，22（2）：157－171.

［7］ BOKHORST 段 C，SLOMP J，GAALMAN C S C，et al.On the who－rule in dual resource constrained（DRC）manufacturing systems［J］.International Journal of Production Research，2004，42（23）：5049－5074.

［8］ YUE H，SLOMP J，MOLLEMAN E，et al.Worker flexibility in a parallel dual resource constrained job shop［J］.International Journal of Production Research，2008，46（2）：451－467.

［9］ HAMEDI M，ESMAEILIAN 段 ，ISMAIL N，et al.Capability－based virtual cellular manufacturing systems formation in dual－Resource constrained settings using tabu search［J］.Computers ＆Industrial Engineering，2012，62（4）：953－971.

［10］ DING Guangtai，TU Bengsheng.Nalysis of variance of output and state of a serial production line with different allocation of buffer capacities［J］.Journal of Nankai University，1999，32（4）：107－114（in Chinese）.［丁广太，涂菶生.串行生产线的状态及输出与其缓冲区的关系分析［J］.南开大学学报，1999，32（4）：107－114.］

［11］ SONG Shigang，LI Aiping，XU Liyun.Buffer capacity optimization in reconfigurable manufacturing system［J］.Computer Integrated Manufacturing Systems，2008，14（10）：1951－1956（in Chinese）.［宋士刚，李爱平，徐云立.可重组制造系统缓冲区容量的优化研究［J］.计算机集成制造系统，2008，14（10）：1951－1956.］

［12］ LI Jingyao，SUN Shudong，HUANG Yuan，et al.Algorithm for dual resource constrained job shop scheduling［J］.Journal of Mechanical Engineering，2010，46（22）：175－181（in Chinese）.［李兢尧 孙树栋，黄 媛，等.双资源约束作业车间调度算法研究［J］.机械工程学报，2010，46（22）：175－181.］

［13］ SUN Zhijun，ZHU Jianying.Intelligent optimization for job shop scheduling of dual－resources［J］.Journal of Southeast University：Natural Science Edition，2005，35（3）：376－381（in Chinese）.［孙志峻，朱剑英.双资源作业车间智能优化调度［J］.东南大学学报：自然科学版，2005，35（3）：376－381.］

［14］ LI Shujuan，LI Yan，LIU Zhigang.Mix optimization scheduling approach for multi－resource job－shop［J］.Journal of Systems Engineering，2007，22（5）：551－555（in Chinese）.［李淑娟，李 言，刘志刚.一类多资源作业车间混合优化调度方法［J］.系统工程学报，2007，22（5）：551－555.］

［15］ LITTL 段 C.A proof for the queuing formula：L＝λ［J］.Operations Research，1961，9（3）：383－389.

［16］ ZHAI Yingni，SUN Shudong，WANG Junqiang，et al.Bottleneck detection method based on orthogonal experiment for Job Shop［J］.Computer Integrated Manufacturing Systems，2010，16（9）：1945－1952（in Chinese）.［翟颖妮，孙树栋，王军强，等.基于正交试验的作业车间瓶颈识别方法［J］.计算机集成制造系统，2010，16（9）：1945－1952.］

［17］ EMMANOUILIDIS C，HUNTER A.Multi－objective evolutionary setting for feature selection and a commonality based crossover operator［C］／／Proceedings of the 2000IEEE International Conference on Evolutionary Computation.Washington，D.C.，USA：IEEE，2000：309－316.