运输能力有限混合流水车间调度的改进拉格朗日松弛算法

轩 华

（郑州大学管理工程学院，河南 郑州 450001）

0 引言

在许多制造系统中，半成品要通过吊车或自动引导车（Automatic Guided Vehicle，AGV）从一台机器运送至另一台机器［1］。然而，很多传统的调度模型都假设在任意两个加工阶段之间有足够的运输机来完成运输任务，即工件j在完成阶段i－1上的加工后可以马上送到阶段i上进行加工。但在实际生产中，由于一个工件必须借助运输机完成相邻两个加工阶段间的传送，并且可利用的运输机及其运输能力都是有限的，上述假设并不成立。

本文研究了协调生产和运输的混合流水车间（Hybrid FlowShop，HFS）调度，其中假设工件具有动态到达特性且运输机能力有限。流程工业中的HFS环境较为常见，如钢铁业、化工业和石化业等。例如钢铁业中的炼钢—精炼生产过程［2］，炼铁阶段生产的铁水通过鱼雷车送到转炉以炼制钢水，然后由吊车将钢水送至精炼阶段进行进一步加工。如图1所示，该过程可归结为带运输问题的HFS结构。由于钢铁业中运送的工件又大又重，假设每台运输机的运输能力为1是合理的［3］。

很多学者对HFS调度进行了研究，然而多数文献都未考虑运输问题。Luo等［4］利用遗传算法求解带处理机和机器维修时间段的两阶段HFS调度，目标是最小化最大完成时间makespan。Behnamian等［5］结合遗传算法和变邻域搜索算法提出一个混合算法求解带顺序有关调整时间的HFS调度，其中加工时间取决于机器和资源，目标是最小化makespan和总资源分配费用；Li等［6］利用两阶段启发式算法求解了带顺序相关调整时间的HFS调度；Nishi等［7］提出结合列生成的拉格朗日松弛（Lagrangian Relaxation，LR）来求解HFS调度，以最小化总加权拖期；Fiqielske［8］提出启发式算法求解带并行异构机和附加资源的两阶段HFS调度，以最小化makespan。

就所查文献可知，考虑生产与运输协调的HFS调度的研究颇少。Naderi等［9］提出改进的模拟退火算法求解带顺序有关调整时间的HFS调度，以使总完成时间和总拖期最小化，其中考虑了从阶段t－1到阶段t之间和从阶段t到阶段t－1的运输时间，以及工件等待运输机返回的时间；Naderi等［10］提出电磁算法求解带顺序有关调整时间和工件无关运输时间的HFS调度，目标是最小化总加权拖期；Tang等［11］从实际炼钢精炼生产过程中提炼出带等待时间和运输的两阶段HFS调度，利用禁忌搜索算法进行求解，以使最大完成时间、空闲时间惩罚和等待时间惩罚之和最小化，或使最大完成时间、空闲时间惩罚和与等待时间有关的热损惩罚之和最小化。

从上述文献可以总结出，现有研究缺乏对求解带运输考虑的HFS调度的LR算法和总加权完成时间问题的探讨。本文的主要工作是对带有限运输能力的动态HFS调度问题建立数学模型，进而设计基于阶段分解的LR来求解；设计动态规划算法来求解分解后的工件带任意权重且有机器不可用时间段的并行同构机子问题。

1 数学建模

1.1 问题描述

所研究的HFS调度问题可描述如下：n个工件在h个加工阶段按相同加工顺序进行加工，至少有一个加工阶段有多台并行同构机；每台机器一次至多加工一个工件，而每个工件只能在一台机器上加工，假设工件动态到达第一个加工阶段；当工件j完成在阶段i的加工后，由一台运输机送到下一阶段i＋1上，这两个阶段间可用的运输机数有Ri，i＋1台，每台运输机一次只能运送一个工件，它将工件送至阶段i＋1后返回阶段i，设从阶段i到阶段i＋1的运输时间为Ti，i＋1，从阶段i＋1到阶段i的返程时间为RTi，i＋1，假设Ti，i＋1和RTi，i＋1为常数，与传送的工件无关且不可忽略不计。

1.2 建模策略

将运输机看作是虚拟机器，则在运输阶段工件的加工时间等于从前一加工阶段到后一加工阶段的运输时间，因此可将考虑运输的原问题转换为与其等价的、不考虑运输但偶数阶段有工件相关不可用机器时间段的调度问题，转换成的阶段数为（2×h－1），且运输阶段总在偶数阶段。

需要注意的是，在转换后的问题中，偶数阶段的机器（运输机）有不可用时间段，这意味着机器不能连续被使用。因为当运输机把工件送到下一加工阶段后，经返程时间后才能继续执行下一运输任务，所以运输机在返程的这段时间内是不能使用的。假设工件［j］和［j＋1］在偶数阶段i的同一台机器l上加工，其中［j］表示加工序列中的第j个位置，则在偶数阶段i上，机器l的不可用时间段从工件［j］在该运输阶段的完成时间Ci［j］的下一时刻开始直到Ci［j］＋rti－1，i＋1变化，其中rti－1，i＋1为转换后问题的返程时间。因此，机器不可用时间段与工件有关，且是变化的。

1.3 模型

基于上述建模策略，建立转换后的调度问题的数学模型如下：

（1）参数

j为工件，j∈Z，Z＝ ｛1，2，…，n｝，其中n是工件数；

［j］l为在机器l上加工的工件序列中的第j个位置，j∈J；

i为阶段，i∈｛1，2，…，s｝，其中s是转换后的包括运输阶段在内的总阶段数；

k为时间，k∈｛1，2，…，K｝，其中K 是时间水平；

mi为阶段i可利用的机器数；

wj为工件j的权重；

pij为工件j在阶段i上的加工时间，在其值偶数阶段上为运输时间，在奇数阶段上为机器上的加工时间；

rj为工件j的释放时间；

rti－1，i＋1为从阶段i＋1到阶段i－1的返程时间，等于RTi／2＋1，i／2，i＝2，4，…，s－1。

（2）变量

Xijk＝1 工件j在时刻k正在阶段i上加工

0｛否则，j∈J，i＝1，2，…，s，k＝1，…，K；

Cij为工件j在阶段i的完成时间，j∈J，i＝1，…，s，它是时间点（Cij＝k表示工序在时间k的末端完成加工）。

利用上述建模策略和参数，对带有限运输能力的动态HFS调度问题建模如下：

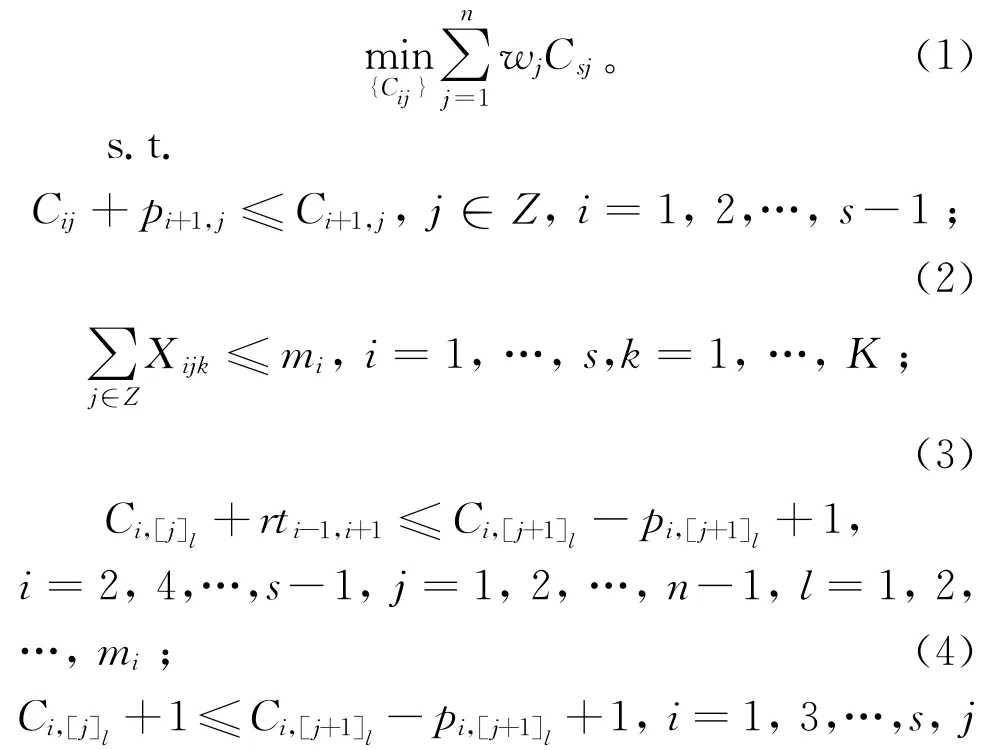
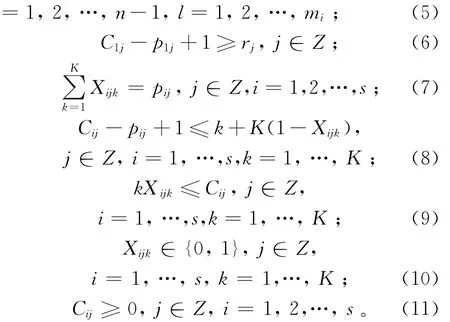
上述模型中，目标函数（1）是最小化总加权完成时间；约束（2）表示工件的工序优先级要求；约束（3）定义了机器能力要求；约束（4）表示在偶数（运输）阶段上，同一台机器（运输机）上加工的相邻两工件之间，只有当前一个工件被送到下一阶段且该机器（运输机）返回到该阶段，才能开始加工（运送）下一个工件；约束（5）说明在奇数阶段上，同一台机器上加工的相邻两工件之间，当前一工件完成在该阶段的加工后，下一个工件可以马上开始它在该机器的加工；约束（6）表示每个工件只有当它到达第一个阶段后才能开始加工；约束（7）～约束（9）定义了加工时间、开始时间和完成时间要求；约束（10）～约束（11）定义了变量取值范围。

2 求解方法——拉格朗日松弛算法

目标函数（1）是加和的形式且约束是线性的，因此可以应用LR算法求解上述模型。然而，如果使用传统的基于工件分解的LR，则由于约束（3）～约束（5）都耦合了不同工件，需要将它们都松弛到目标函数中，而松弛的约束数越多，得到的原问题的下界越松［12］。因此，本章设计了基于阶段解耦的LR算法来求解上述模型，该算法首次由Tang等［13］提出并用于求解一般的不考虑运输和工件动态特性的HFS调度。

2.1 拉格朗日松弛

从1.3节可以看出，只有约束（2）耦合了不同阶段，因此利用拉格朗日乘子｛πij｝松弛该约束到目标函数中，从而形成LR问题：

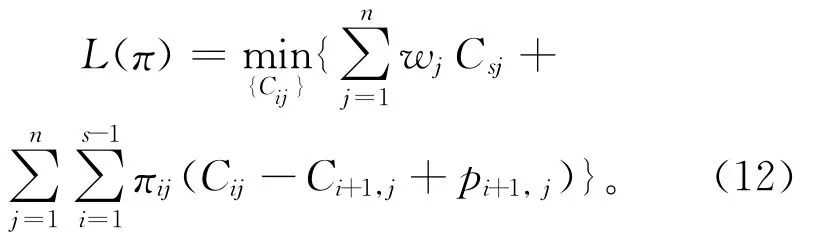
上述目标函数需满足式（3）～式（11）和

πij≥0，i＝1，2，…，s－1，j∈Z。 （13）式中：π是由｛πij｝组成的非负拉格朗日乘子向量，L（π）是乘子函数，定义为拉格朗日对偶。因此，拉格朗日对偶问题为

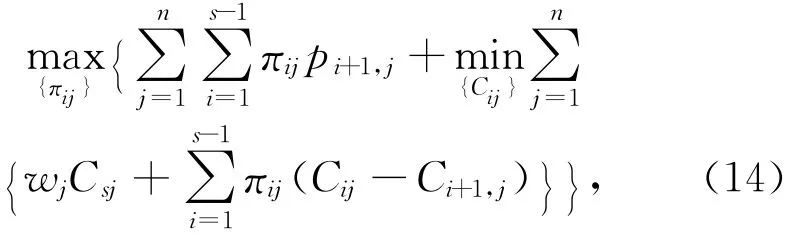
满足式（3）～式（11）和式（13）。

给定｛πij｝，上述松弛问题可以分解为多个阶段级子问题，每个子问题对应一个阶段。阶段i（i∈｛1，…，s｝）的子问题可以表示为

利用LR算法求解上述模型的过程如图2所示。下面将详细描述对偶问题的求解、可行解的构造和子问题的求解。

2.2 更新拉格朗日乘子和构造可行解

每次迭代仍应用次梯度算法更新拉格朗日乘子：

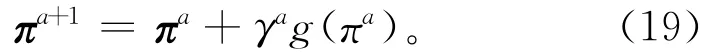
式中：a为迭代数；γa为第a次迭代的步长；g（πa）为L（π）的次梯度，其值等于（Cij－ Ci＋1，j＋ pi＋1，j）。γa定义为

式中：L＊为最优解，由迄今为止得到的最好可行目标函数值来估计；La是第a次迭代的L的值。

当对偶间隙非常小或迭代数达到限制值时程序停止。因为每次迭代从松弛问题得到的解对于原问题来说常是不可行解，所以利用两阶段启发式将不可行时间表转换成可行时间表。在第一阶段，对于阶段i（i＝1，…，s），按照松弛问题中工序开始时间的增序排列各个工件，根据形成的列表依次将所有工件安排到可利用的机器上；在第二阶段，通过两两交换改进上述得到的可行解。

3 求解带机器不可用时间段的并行同构机子问题的动态规划

第2.1节所得到的拉格朗日子问题是带机器不可用时间段和工件动态到达的并行同构机调度问题，目标是最小化总加权完成时间（其中权重是任意值），且机器不可用时间段与工件有关。Tang等［13］提出动态规划算法求解并行同构机调度问题，但该研究未考虑机器的不可用时间段和工件的动态特性，即假设在任一阶段的机器l上工件［j＋1］可在Ci［j］＋1时刻立刻开始加工，而且所有工件在计划时间范围一开始就可利用。对任一阶段i，该研究证明了子问题中的工件在机器l上需要按照带正权重的工序子集、带零权重的工序子集、带负权重的工序子集的顺序进行调度，而且在带正负权重的工序子集中的工序必须按照加权最短加工时间（Weighted Shortest Processing Time，WSPT）规则进行排列。

然而，本文研究的子问题中，在偶数阶段上机器l在时间段［Ci［j］＋1，Ci［j］＋rti－1，i＋1］上不可用于加工（运送）工件［j＋1］，而且工件［j］在时刻rj到达第一个加工阶段后才能开始加工。基于Tang等［13］的相关结论，提出下面的性质和引理，使其提出的动态规划可推广至解决带机器不可用时间段和工件动态到达特征的同构并行机调度问题（证明过程参照文献［13］）。

性质1 令Gip，Gio和Gin分别表示在阶段i机器l上的带正权重的工序子集、带零权重的工序子集和带负权重的工序子集，则在最优解中，这三组子集必须在机器l上按照Gip—Gio—Gin的顺序进行调度。在偶数阶段，Gip和Gin内的工序必须按照（pij＋rti－1，i＋1）／＾wij的升序排列；在奇数阶段，Gip和Gin内的工序必须按照WSPT的顺序排列，而Gio内的工序可任意排列。

引理1 令O表示已经分配到阶段i上某台机器l的工序集合。将工序y插入到O内所有工序之前，若i＝2，4，…，s－1，则 ∑＾wijCij将增加W（O）（piy＋rti－1，i＋1）＋＾wiypiy，否则 ∑＾wijCij将增加（W（O）＋＾wiy）piy，其中W（O）表示集合O内所有工序的总权重。

基于以上性质和引理，可将动态规划的递归关系式归结如下：

分别按照（pij＋rti－1，i＋1）／＾wij和pij／＾wij的增序排列偶数阶段的所有工序和奇数阶段的所有工序，令V（j′，Wi1，Wi2，…，Wimi）表示阶段i上包含从第n道工序到第j′道工序的部分时间表的最小总加权完成时间，其中Wil是分配到阶段i的机器l上的所有工序的总权重。

边界条件：

对在阶段i上所有的j′，V（j′，0，…，0）＝0。

递归关系式：

4 仿真测试

对所设计的算法用C语言编程并在微机（Pentium（R）1.73GHz）上运行，当迭代数达到最大限制500或对偶间隙小于一个很小的数（设为0.5%）时程序停止。计算结果通过对偶间隙和CPU时间来衡量，其中对偶间隙由可行解的目标值与对偶函数的目标值之差除以对偶函数目标值，然后转换成百分比得到。

在基于阶段分解的LR算法中，分解后的阶段级子问题数为s个，乘子数为n×（s－1），利用动态规划求解子问题时，其每个阶段的状态总数为mi，复杂度为O（（n－1）mi2）。而对于传统的基于工件分解的LR算法，分解后的工件级子问题数为n个，乘子数为s×K，利用动态规划求解子问题时，其每个阶段的状态总数为K，复杂度为O（（s－1）K2），且若采用基于工件分解的LR算法，则需要松弛三组约束（3）～约束（5），这会使下界较松，进而使对偶间隙较大。由以上性能可知，从子问题数、存储空间、动态规划的复杂度和要松弛的约束数上，基于阶段分解的LR算法都有较显著的优势，因此本章主要测试基于阶段分解的LR算法来检查其有效性。

4.1 算例

通过测试小规模问题的一个实例，说明由LR算法得到的可行时间表。令n＝6，mi＝3，s＝3（包括运输阶段），运输时间和返程时间设为4，K设为所有工件在各阶段（包括运输阶段）的加工时间之和，其他参数如表1所示。执行算法可以得到该问题的近优解，其调度甘特图如图3所示。

表1 实例数据

4.2 仿真实验

该实验测试了所提出的LR算法求解不同规模HFS调度问题的性能。问题实例随机产生如下：令n＝ ｛20，50，70，100｝，s＝ ｛3，5，7｝（含运输阶段），mi＝｛3，4，5｝；每个工件的加工时间和权重均由［1，10］均匀分布随机产生，工件释放时间满足［1，5］的均匀分布，运输时间ti－1，i＋1和返程时间rti－1，i＋1满足［4，6］之间的均匀分布，时间水平K 设为所有工件的加工时间之和（含运输阶段）。n，s，mi共有36个组合，对每个组合随机产生和测试10个不同的实例，故本节共产生和使用360个测试实例。

计算结果如表2所示，显示于表1中的每个数（除最后一行外）都是所测得相同规模的10个实例的性能平均。

续表2

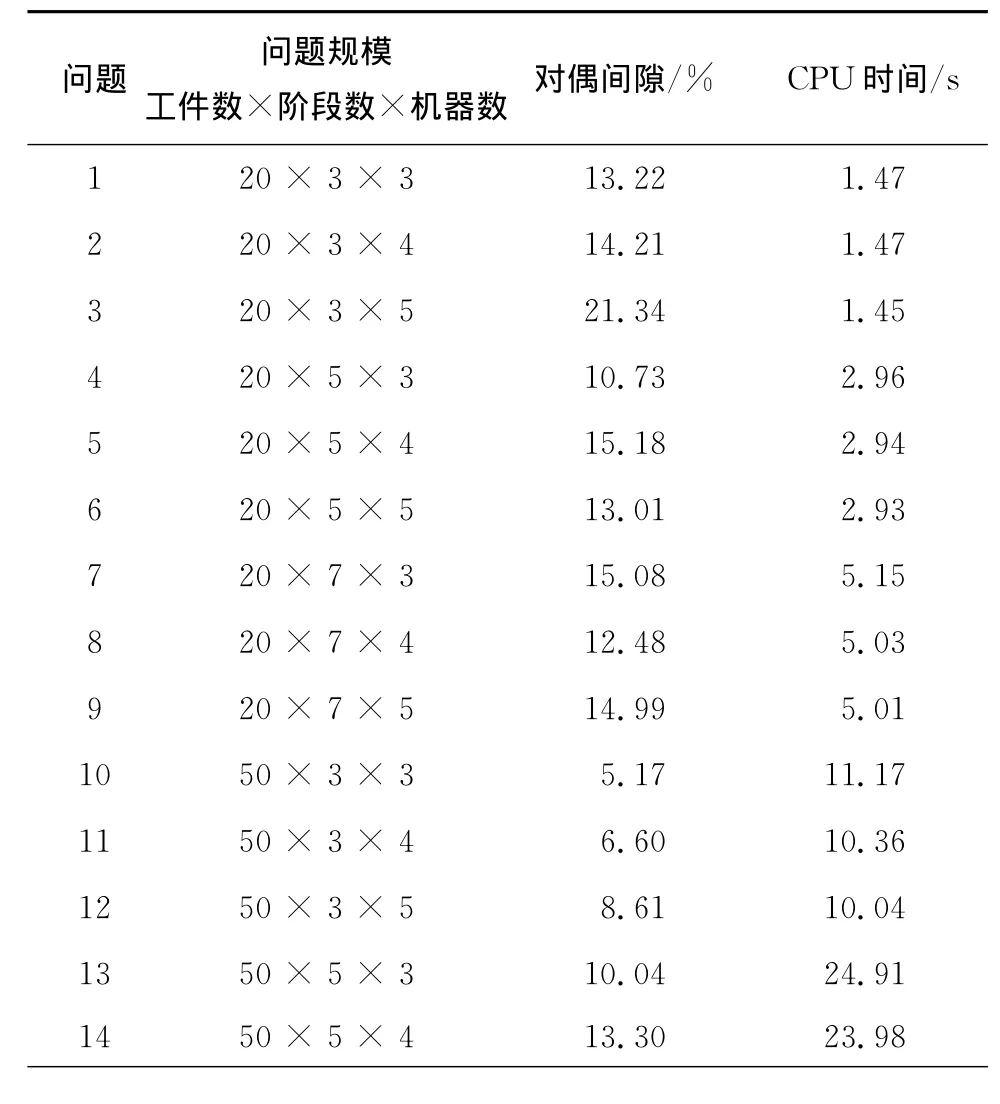
表2 不同规模问题的测试结果

从表2可以得出如下结论：

（1）所有实例在不到1min的计算时间内得到的平均对偶间隙为12.44%。这说明对于所研究的带有限运输能力和工件动态特性的复杂调度问题，所设计的LR算法能够在较短的运行时间内得到可接受的近优解。

（2）相同工件数条件下，当阶段数增加时，因为阶段数增多使得分解后的子问题数增加，从而使问题难以求解，所以解的质量会变差，而且运行时间也会加长。

（3）对于70和100个工件的大规模问题，LR算法平均耗时分别为69.55s和122.10s，得到的平均对偶间隙分别为11.67%和10.59%。因此当问题规模较大时，所设计的LR算法表现出更大的求解潜力。

5 结束语

本文研究了运输和生产协调的动态HFS调度问题，考虑了实际生产中运输机能力有限的要求，目标是最小化总加权完成时间。将每台运输机视为虚拟机器，从而将运输阶段转换为虚拟的加工阶段，进而对转换后的不考虑运输能力但带与工件有关的机器不可用时间段的动态HFS调度问题建立数学模型。基于阶段分解提出了LR算法对该问题进行求解，对分解后的带机器不可用时间段和工件动态特性的并行同构机调度，问题设计了动态规划算法进行求解。数据实验表明，所设计的LR算法能够在较短的运行时间内产生可接受的近优解。进一步的研究可推广至运输能力超过1的HFS调度问题，以使该算法也适用于其他流程工业。

［1］ SOUKHAL A，OULAMARA A，MARTINEAU P.Complexity of flow shop scheduling problems with transportation constraints［J］.European Journal of Operational Research，2005，161（1）：32－41.

［2］ TANG 段 ，LUH L H，LIU L U，et al.Steel－making process scheduling using Lagrangian relaxation［J］.International Journal of Production Research，2002，40（1）：55－70.

［3］ TANG L，GONG H.A hybrid two－stage transportation and batch scheduling problem［J］.Applied Mathematical Modelling，2008，32（12）：2467－2479.

［4］ LUO H，HUANG 段 ，ZHANG Z A，et al.Hybrid flowshop scheduling with batch－discrete processors and machine maintenance in time windows［J］.International Journal of Production Research，2011，49（6）：1575－1603.

［5］ BEHNAMIAN J，FATEMI GHOMI 段 T.Hybrid flowshop scheduling with machine and resource－dependent processing times［J］.Applied Mathematical Modelling，2011，35（3）：1107－1123.

［6］ LI L，WANG 段 ，HUO H O.Hybrid flowshop scheduling with setup times for cold treating process in Baoshan iron ＆steel complex［C］／／Proceedings of 2010International Conference on Logistics Systems and Intelligent Management.Washington，D.C.，USA：IEEE，2010，1：357－363.

［7］ NISHI T，HIRANAKA Y，INUIGUCHI M.Lagrangian relaxation with cut generation for hybrid flowshop scheduling problems to minimize the total weighted tardiness［J］.Computers and Operations Research，2010，37（1）：189－198.

［8］ FIGIELSKA E.A genetic algorithm and a simulated annealing algorithm combined with column generation technique for solving the problem of scheduling in the hybrid flowshop with additional resources［J］.Computers and Industrial Engineering，2009，56（1）：142－151.

［9］ NADERI B，ZANDIEH M，KHALEGHI GHOSHE BALAGH A，et al.An improved simulated annealing for hybrid flowshops with sequence－dependent setup and transportation times to minimize total completion time and total tardiness［J］.Expert Systems with Applications，2009，36（6）：9625－9633.

［10］ NADERI B，ZANDIEH M，SHIRAZI 段 H A.Modeling and scheduling a case of flexible flowshops：Total weighted tardiness minimization［J］.Computers and Industrial Engineering，2009，57（4）：1258－1267.

［11］ TANG 段 ，GUAN J，HU G A.Steelmaking and refining coordinated scheduling problem with waiting time and transportation consideration［J］.Computers ＆Industrial Engineering，2010，58（2）：239－248.

［12］ XUAN H，TANG 段 .Scheduling a hybrid flowshop with batch production at the last stage［J］.Computers ＆ Operations Research，2007，34（9）：2718－2733.

［13］ TANG 段 ，XUAN H，LIU X A.A new Lagrangian relaxation algorithm for hybrid flowshop scheduling to minimize total weighted completion time［J］.Computers ＆ Operations Research，2006，33（11）：3344－3359.