多载具自动化存取系统作业调度优化

杨 朋，缪立新，秦 磊

（清华大学深圳研究生院现代物流研究中心，广东 深圳 518055）

0 引言

多载具（multi－shuttle）自动化存取系统（Automated Storage and Retrieval System，AS／RS）是一种高吞吐量高柔性的新型仓储系统，多载具AS／RS堆垛机一次行程可以同时存放和取出多个货物单元。与单载具AS／RS相比，多载具AS／RS能够有效缩短无效空载时间，提高存取货作业效率，在当今多品种小批量的制造配送环境下具有较大的应用潜力，正得到越来越多的仓库及配送中心的关注和应用。

多载具AS／RS按照作业周期（operation cycle）模式来处理存取货作业，一个作业周期就是多载具堆垛机的一个子行程，该子行程从进出货口（I／O point）装载着待存货物出发，分别访问对应的存货货位和取货货位，然后载着取出的货物返回进出货口。基于这一特点，多载具AS／RS存取货作业调度优化的关键就是如何将存取货作业按照作业周期合理分组。

目前，有关多载具AS／RS的研究集中在绩效评价、货位分配和存取货作业排序。绩效评价方面主要通过推导行程时间模型，对双载具（doubleshuttle）AS／RS与单载具 AS／RS［1－4］、三载具（triple－shuttle）AS／RS与单载具 AS／RS［5］的绩效进行对比分析。也有文献通过仿真分析方法对多载具AS／RS的绩效进行评价［6－7］。货位分配多关注不同情形下货位分配模型及求解算法的设计研究。文献［8］抽象建立了多载具AS／RS存取货位分配的数学模型，并设计了基于修正最近邻点策略的遗传算法求解模型。文献［9］提出了考虑作业路径的多载具AS／RS货位分配优化问题的建模和求解方法，并设计了两阶段禁忌搜索算法来获得单作业周期下的货位分配方案。文献［10］则从应用成本的角度分析了双载具AS／RS货位分配策略的选择。存取货作业排序方面，文献［11］将给定存取货位的多载具AS／RS存取作业排序归纳为有载货量限制的车辆路径问题（Capacitated Vehicle Routing Problems，CVRP），并开发了对应的精确算法对相应的线性松弛模型进行求解。文献［12］延续了文献［11］的研究，将禁忌算法与前述精确算法结合起来，改进了模型的下界。文献［13］则在文献［11］和文献［12］的基础上开发了基于拉格朗日松弛方法的精确算法对问题进行求解。另外，有些仓库和配送中心中补货操作（存货）和货物消耗作业（取货）通常发生在不同的班次，文献［14］针对这一情况，研究提出了基于班次的双载具AS／RS作业排序方法，以提高吞吐量。

已有研究中，文献［11－13］涉及多载具 AS／RS存取货作业调度问题，但是只从存取货作业排序角度进行了探讨。对存取货作业进行合理分组是多载具AS／RS存取货作业调度优化的关键。由于存在存货和取货两种类型作业，对作业的分组需要考虑作业分解和作业配对问题，另外每个作业周期内需要处理多个作业，考虑多载具载货量的限制，处理作业的顺序也会有相应约束。文献［11－13］忽略了作业分解和作业配对的影响，具有一定的局限性。本文将从作业分解、作业配对和作业排序三个子问题联合优化的角度对多载具AS／RS作业调度进行研究，最小化多载具AS／RS完成存取货作业的总行程时间，以更加接近作业实际的角度来提高存取作业效率。

1 问题描述

n载具自动化存取系统下，存取货作业需要通过配对分组，由堆垛机的多个子行程来依次处理，每个子行程对应一个作业周期。一个作业周期可同时处理小于等于n个存货作业和小于等于n个取货作业。为提高多载具AS／RS的利用率，在存取货作业充足的情况下，每个作业周期往往“满载”即对应处理n个存货作业和n个取货作业。多载具AS／RS作业调度优化的目的，就是寻找最优的作业分组方案，使得完成作业的总行程时间最短。

多载具AS／RS存取作业调度问题（Storage／Retrieval Scheduling Problem，SRSP）中，假设V＝｛1，2，…，M，M＋1，…，2 M｝为存取货作业集合，其中Vs＝｛1，2，…，M｝为存货作业集合，Vr＝｛M＋1，…，2 M｝为取货作业集合，｛0｝代表进出货口。M＝nm，其中n为载具数量，m为完成存取作业所需的作业周期数量。SRSP目标函数是寻找总行程时间最短的作业周期集合划分方案，作业周期集合中，每个作业周期对应一个子行程，该子行程从进出货口出发，按照顺序执行完n个存货作业和n个取货作业后再返回进出货口，而且为了满足堆垛机载货量的限制，行程中任意时刻已完成的存货作业都必须大于或等于已完成的取货作业。

考虑单元货物型（unit load）多载具AS／RS，堆垛机装载相应货物单元在既定货位和进出货口之间移动，完成存取货作业。研究中做以下假设：货物采用固定存储策略（dedicated storage）存放；给定时间段内的存取货作业已知，且对应的货位信息已知；多载具堆垛机可以同时在垂直和水平方向移动，速度是恒定值，两个货架货位间的时间距离采用切比雪夫距离，且满足三角不等式（triangle inequality）关系；货物装卸时间忽略不计。

采用无向图G＝｛V′，E｝来描述作业的集合及作业对应货位之间可能的连接，其中V′＝｛0｝∪V，V ＝Vs∪Vr，E＝ ｛（i，j）｜i，j∈V｝。约定如下符号：dij为货位i和货位j的行程时间间距（i，j＝0，1，…，2 M），即先后执行作业i，j的行程时间，dij＝dji；xij为决策变量，xij＝1表示子行程中包含i直接到j的路径，否则xij＝0。另外，为了表达作业的集合划分及作业的访问顺序，增加3下标索引的决策变量zilk，若作业i作为第k个子行程中的第l个点被访问到，则zilk＝1，否则zilk＝0。多载具AS／RS存取作业调度问题可建模如下：

存取作业调度的整数规则问题（SRSP Integer Programming problem，SRSP－IP）的目标函数为

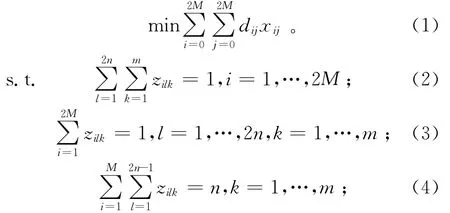
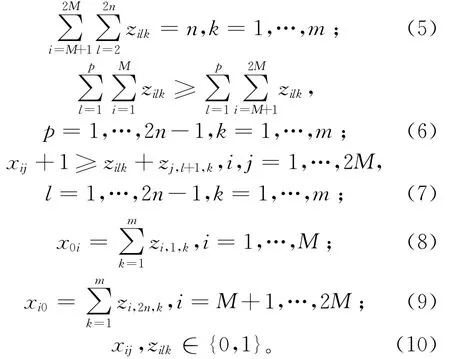
其中：约束（2）确保每个作业对应的货位都会被访问到；约束（3）表示每个子行程中的每个顺序位都会指派货位进行访问；约束（4）确保每个子行程会执行n个存货作业，即访问n个存货货位；约束（5）确保每个子行程同时会执行n个取货作业，即访问n个取货货位；约束（6）是多载具堆垛机载货量限制约束，即任何时刻，行程中已完成的存货作业数量大于或等于已完成的取货作业数量；约束（7）确保当xij＝0时vi和vj不会在子行程中顺次被访问，当xij＝1时vi和vj才有可能在在子行程中顺次被访问到；约束（8）和约束（9）确保每个子行程从进出货口出发，并最终回到进出货口；约束（10）表示决策变量为0－1变量。

SRSP－IP模型决策变量数为O（M2），约束数量为O（M3），该0－1规划问题规模随M的增加会急剧膨胀。为便于分析问题的复杂度，以子行程的选择为决策变量对SRSP－IP模型进行转化。

SRSP－IP可看作在全体可行子行程集合中，所选出的最优的m个子行程能够覆盖所有的存取货作业，且行程时间最短。约定如下符号：Ω为所有可行子行程的索引集合，cr为完成第r个子行程所需的行程时间，W＝（wir）为“作业—行程”矩阵，W∈ ｛0，1｝V×Ω，其中wir＝1表示作业i在第r个行程被执行，否则wir＝0。决策变量为yr，yr＝1表示选择第r个子行程，否则yr＝0。以子行程的选择为决策变量的模型可表示如下：

行程选择的整数规划问题（Routing Selection Integer Programming problem，RS－IP）的目标函数为

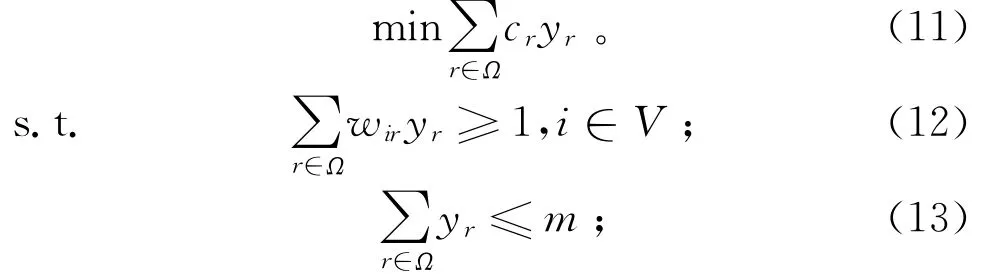
其中：约束（12）保证每个作业都会被执行，即每个作业对应的货位都会被访问到；约束（13）确保被选中的子行程数量为m。

2 问题复杂度分析

由于涉及作业分解、作业配对和作业排序三个问题，多载具AS／RS存取作业调度优化问题的解空间规模可由三类问题组合数的乘积求得。其中将

M个作业进行分解，每组划分n个作业，这种分组的组合数可表示为

为保证堆垛机行程中不超过载货限制，任一可行的子行程都需满足任意时刻已完成的存货作业都必须大于或等于已完成的取货作业。基于此，可行子行程的数量可以通过以n为变量的卡特兰数Cn来计算获得：

根据计算复杂性理论，为研究优化问题的计算复杂性，首先需要将优化问题转化为判定问题（decision problem）［15］。第1章已给出RS－IP问题的优化问题形式，其对应的判定问题定义如下：

（1）参数 Z＋为正整数集合。

（2）实例 存取货作业集合V共有2M个元素，其中有M个存货作业，M个取货作业，M＝nm。F为集合V的子集族（即子集的集合），F中的每个元素Si（i＝1，2，…，H）为包含n个存货作业和n个取货作业的子集，即对应一个可行子行程，每个元素Si关联一个行程时间ci，ci∈Z＋。给定一个数C∈Z＋。

（3）问题 是否存在子集F′⊂F，满足存取作业集合V中的每个作业都只精确分布在F′的一个元素中，且满足

证明RS－IP的判定问题为非确定多项式困难（Non－deterministic Polynomial hard，NP－hard）问题，可分为以下几步：

定理1 RS－IP问题为NP－hard。

证明

（1）选择一个已

知的NP－hard问题或 NP－complete问题

精确匹配（Exact Cover，EC）问题是一个已知的 NP－complete［16］。EC 问 题 的 判 定 问 题 定 义如下：

1）实例 给定有限集合V和集合V的子集族F。

2）问题 是否存在子集F′⊂F，满足集合V中的每个元素都只精确分布在F′的一个子集元素中。

为便于理解，给出EC问题的一个数值实例V＝ ｛1，2，3，4，5，6｝，F ＝ ｛｛1，4｝，｛2，4｝，｛3，5｝，｛3，6｝，｛1，5｝，｛3，4｝｝。上述EC问题的答案为“是”，可取F的子集F′＝ ｛｛2，4｝，｛3，6｝，｛1，5｝｝，满足集合V中的每个元素都只精确分布在F′的一个子集元素中。

（2）将EC问题多项式归约为RS－IP问题

给定存取货作业集合V，集合V共有2 M个元素，其中有M个存货作业，M个取货作业，M＝nm。F为集合V的子集族，F中的每个元素Si（i＝1，2，…，H）为包含n个存货作业和n个取货作业的子集。假设存在子集F′⊂F，满足存取作业集合V中的每个作业都只精确分布在F′的一个元素中，＝m。基于F′构造RS－IP问题，约定

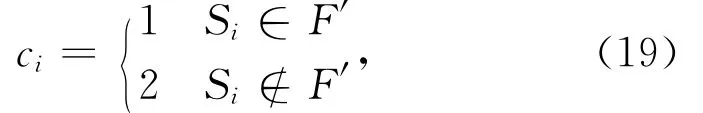
且取C＝m。不难看出，在子集族F中，行程时间最短的子集为F′，且行程时间不超过m，如果在F′之外选择元素，则其行程时间将至少为m＋1。显然，基于F′构造RS－IP问题的时间为多项式时间。因此EC问题可多项式归约为RS－IP问题。

（3）将RS－IP问题归约为EC问题

显然满足。

（4）验证RS－IP是否是NP问题

给定RS－IP问题的子行程集合，验证该子行程集合是否能够覆盖每一个作业需O（Ω ）的时间，验证对应的行程时间总和是否不超过C需要O（Ω ）的时间。Ω ＝s（M，n），由式（18）计算得到，它与M成阶乘关系，不能在多项式时间内验证子行程集合的可行性。因此不能判断RS－IP是否为NP－hard。

综上，RS－IP问题为NP－hard，定理得证。

3 算法求解

通过第2章的分析得知多载具AS／RS作业调度问题是NP－hard，本章设计遗传模拟退火的启发式算法对问题进行求解。遗传算法是借鉴生物进化规律演化而来的计算技术，强调的是两代之间的进化关系，但其交配有可能丢失最优解，易陷入局部极小。模拟退火算法是基于物理中固体物质的退火过程，从某一较高初温出发，伴随温度参数的不断下降，结合概率突跳特性，在解空间中随机寻找目标函数的全局最优解。将模拟退火的思想融入遗传算法，构成遗传模拟退火算法，通过种群操作自动获取和调整优化的搜索空间，根据温度变化调整适应函数的加速特性，比遗传算法具有更大的选择范围，可以有效避免局部极小。遗传模拟退火算法的设计与具体问题关联密切，下面对求解多载具AS／RS的遗传模拟退火算法的关键技术进行说明，然后给出算法流程。

染色体编码方面，本文采用存取货作业排序的编码方式，且需要满足堆垛机载货量限制的约束条件。例如m＝2，n＝3，Vs＝｛1，2，3，4，5，6｝为存货作业集合，Vr＝｛7，8，9，10，11，12｝为取货作业集合，一个可行的染色体编码示意如图1所示。

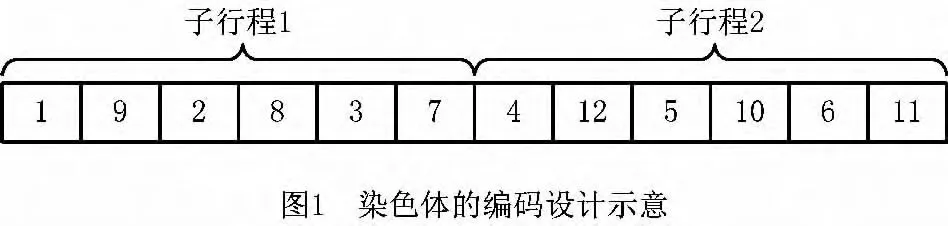
初始种群根据编码结构，按照满足堆垛机载货量限制的约束规则（任意时刻已完成的存货作业必须大于或等于已完成的取货作业）随机生成。初始种群中的染色体可按以下步骤生成：

步骤1 初始化已完成的存货作业数量Cur＿storage＝0，已完成的取货作业数量Cur＿retrieval＝0，已完成的子行程数量Num＿tour＝1，子行程内作业的索引index＝1，Vs，Vr，m和n分别为存货作业集合、取货作业集合、子行程数和载具数。数组Chrom代表染色体，索引i＝1。

步骤2 如果index＝2×n＋1，Num＿tour＝Num＿tour＋1，index＝1；否则转步骤4。

步骤3 如果Num＿tour＝m＋1，则结束；否则转步骤4。

步骤4 如果Cur＿storage＝Cur＿retrieval，则从Vs随机选取作业k，Chrom（i）＝k，Vs＝Vs－｛k｝，Cur＿storage＝Cur＿storage＋1，i＝i＋1；否则从Vs∪Vr中随机选取作业k，Chrom（i）＝k，i＝i＋1，如果k∈Vs，则Vs＝Vs－｛k｝，Cur＿storage＝Cur＿storage＋1，否则Vr＝Vr－｛k｝，Cur＿retrieval＝Cur＿retrieval＋1。

步骤5 index＝index＋1，转步骤2。

考虑到计算代价及后续选择交配操作的方便性，种群规模取编码长度的2或4等偶数倍。结合模拟退火和轮盘赌的方法对种群进行选择操作。交叉操作采用部分匹配交叉方法，先随机产生两个交叉点，定义两个点之间的部分为匹配区域，将两个父串的匹配区域交叉（如图2），然后再遍历重复，根据匹配区域内的位置映射关系逐一进行交换，最后再进行子串解的可行性检查。

为避免早熟，增加遍历性，算法在个体染色体中随机选取两个交叉位进行交换变异，为保证个体为可行解，随机选取两个交叉位对应的作业应同属一种类型的作业集合，如同属存货作业集合或同属取货作业集合。算法流程如下：

步骤1 给定种群规模MAXPOP，k＝0；初始温度tk＝t0，种群POP（k）。

步骤2 若k达到最大种群迭代次数MaxIteration，则停止计算；否则，对种群POP（k）中每一个染色体i∈POP（k）的邻域随机选状态j∈N（i）（染色体的邻域采用在保证解可行的前提下随机交换两个作业点的方法生成），计算Δfij＝f（j）－f（i），其中f（i）为状态i的目标值。若Δfij≤0，则接受j，否则若exp（－Δfij／tk）＞random（0，1）则接受j，否则拒绝j。重复这一过程，选出新种群NewPOP1（k＋1）。

步骤3 在NewPOP1（k＋1）中计算适应度函数fi（tk）＝exp（－（f（i）－fmin）／tk），其中fmin是NewPOP1（k＋1）中的最小值，按照轮盘赌方法由适应度函数决定的概率分布，从NewPOP1（k＋1）中随机选MAXPOP个染色体，形成种群New－POP2（k＋1）。

步骤4 按遗传算法方法对NewPOP2（k＋1）进行交配，得到CrossPOP（k＋1），再变异得到MutPOP（k＋1）。

步骤5 tk＋1＝0.8tk，k＝k＋1，POP（k）＝Mut－POP（k＋1），转步骤2。

4 数值实验

为评价算法性能，设计一系列具有不同参数场景的问题进行数值实验。设W和H 分别为货架的长度和高度，堆垛机水平方向的速度和垂直方向的速度分别为vx和vy，堆垛机分别在水平方向和垂直方向遍历整个货架所需的行程时间为th＝W／vx和tv＝H／vy。设Z＝max｛th，tv｝，b＝min｛th／Z，tv／Z｝分别表示遍历货架所需的行程时间和货架形状因子。考虑到通用性，设Z＝1，对货架比例进行归一化。每个货位关联一对水平行程时间和垂直行程时间（hk，vk），任意两个货位间的行程时间为

式中Δ为足够大的正数。

具体的参数场景设置为：载具数量n＝2，3，4；货架形状因子b＝0.2，0.4，0.6，0.8，1；作业周期（子行程）数量m＝1，2，3，4。每个货位关联一对水平行程时间和垂直行程时间（hk，vk），hk和vk分别按照正态分布U（0，1）和U（0，b）随机生成。启发式算法采用 MATLAB 7.1软件来编程实现，采用CPLEX 12.2软件求解问题的最优解。数值实验在AMD 2.30GHz CPU和1GHz内存的个人计算机环境下运行。

表1给出了不同货架形状因子（b＝0.2，0.4，0.6，0.8，1）情况下，遗传算法和本文所提遗传模拟退火算法在求解中小规模问题（n＝2，m＝3）下的精确度和计算效率，也给出了采用CPLEX求解最优解的计算时间。每个实验场景随机生成10组数据，分别记录两种算法求得的最优解数量（Num＿opt）和与最优解之间的偏差。从实验结果可见，遗传模拟退火算法在不同货架形状因子下对遗传算法都具有较大的改进，算法的精确度和计算时间受货架形状因子b的影响微小，不具有显著的敏感度。

表2给出了货架形状因子固定时，遗传算法和本文所提遗传模拟退火算法在求解中小规模问题下的精确度和计算效率，同时给出了CPLEX求解最优解的计算时间。同样地，每个实验场景随机生成10组数据，分别记录两种算法求得的最优解数量（Num＿opt）和与最优解之间的偏差。可见，在问题规模变大时，CPLEX求解最优解的计算时间急剧增加。在计算结果的质量方面，遗传模拟退火算法对遗传算法具有较大的改进，与最优解的偏差为0%～0.83%，具有较稳定的精确度。随着问题规模的增大，遗传模拟退火算法的计算时间随之增加，但都在10s以内，具有较高的求解效率。

在大规模问题情形下（m≥5），本文比较了遗传算法和本文所提遗传模拟退火算法的计算结果质量和计算时间。同样，每个实验场景随机生成10组数据，表3记录了采用两种算法所获得的平均行程时间和平均耗费的计算时间。从实验结果可见，遗传模拟退火算法耗费的计算时间稍高于遗传算法，但计算结果质量均优于遗传算法，根据问题规模的不同，计算结果有2%～17%的改进。

表1 不同货架形状因子情况下的算法性能分析（n＝2，m＝3）

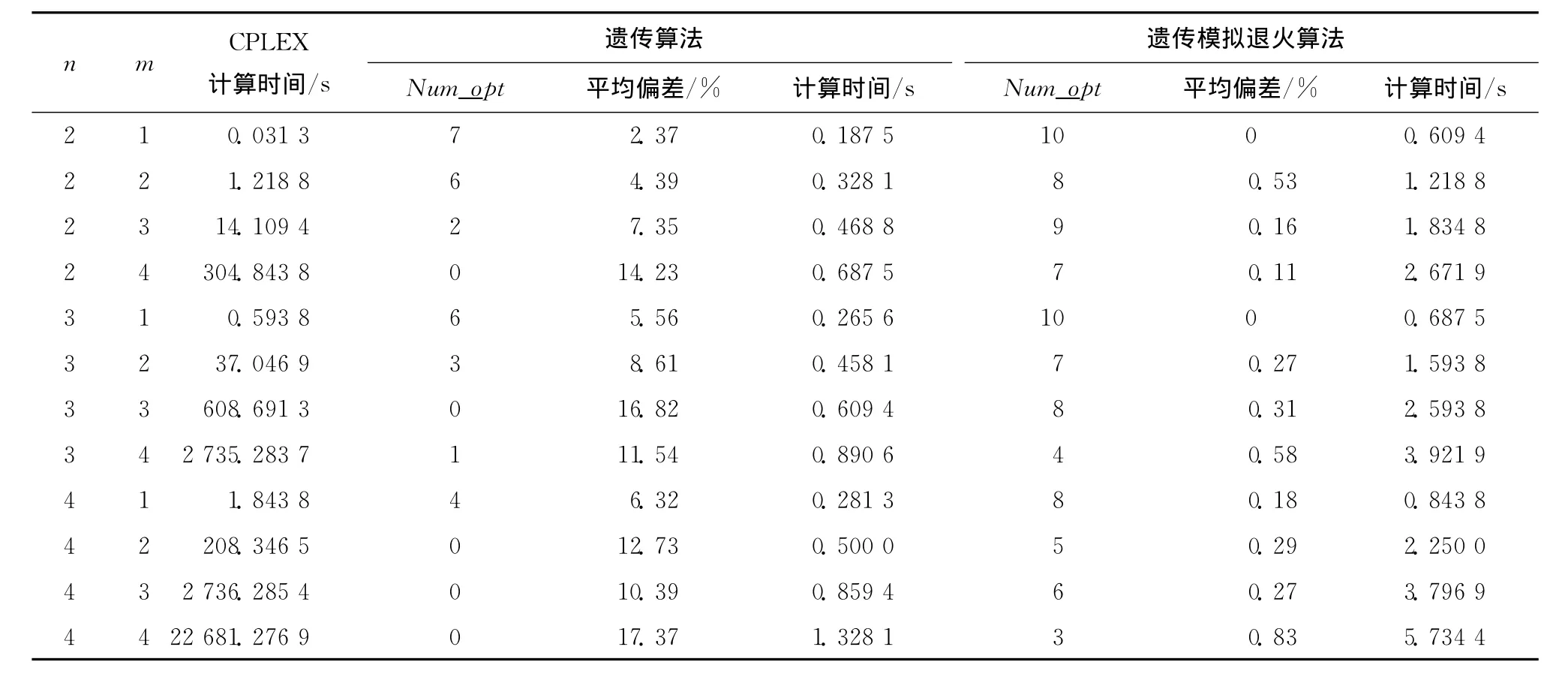
表2 不同问题规模情况下的算法性能分析（b＝0.8）

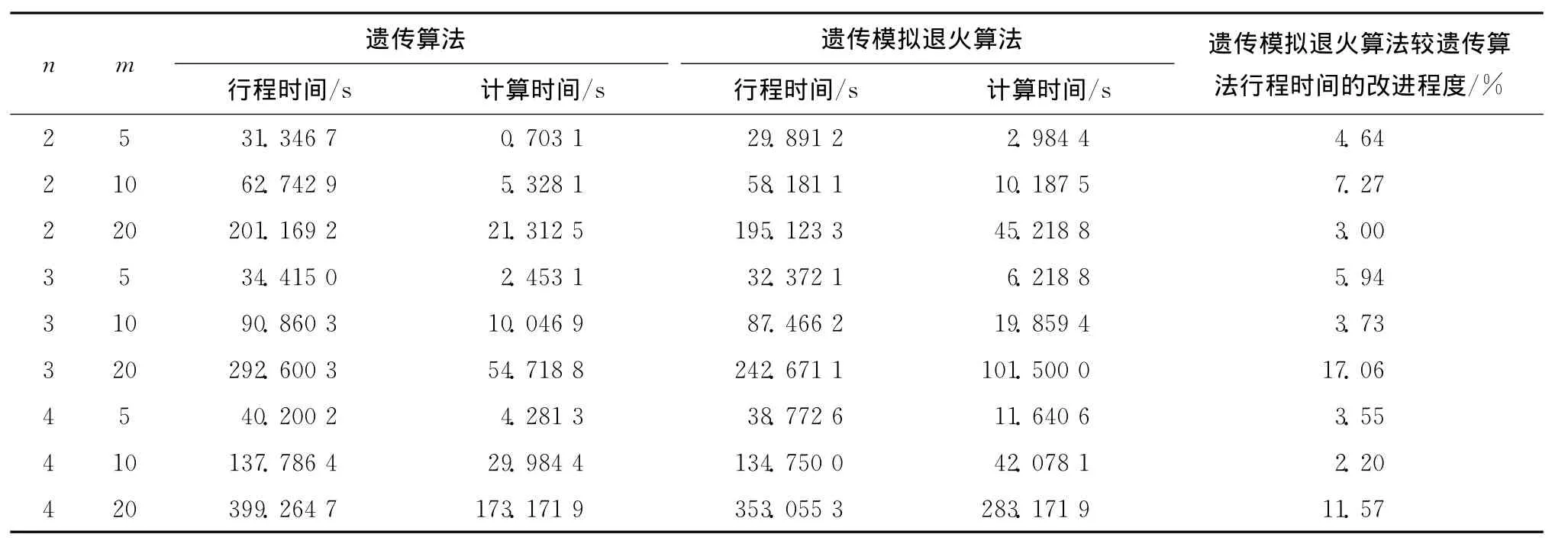
表3 大规模问题情况下的算法性能分析（b＝0.8）

5 结束语

本文在多载具AS／RS存取货作业排序研究的基础上，增加考虑了作业分解和作业配对的影响。从作业分解、作业配对和作业排序三个子问题联合优化的角度，探讨了多载具AS／RS的作业调度优化问题。对问题的复杂度进行了分析，证明了问题为NP－hard，设计了遗传模拟退火算法对问题进行求解。通过数值实验验证了算法的有效性，实验结果表明在不同规模问题下，算法都能够在合理的时间内获得高质量的调度方案，从而有效缩短了完成存取货作业的行程时间。算法具有较好的精确度和求解效率，而且算法的性能对货架形状因子参数不敏感。下一步研究可以考虑货位分配和货物停留时间因素影响，在共享货位存储策略下，按照货物停留时间精确地调度每个指令的货位分配及作业顺序，以保证在指令执行不发生干涉的前提下达到行程时间最短的优化目的。

［1］ SARKER 段 ，SABAPATHY A，LAL S B，et al.Performance evaluation of a double shuttle automated storage and retrieval system［J］.Production Planning ＆Control：The Management of Operations，1991，2（3）：207－213.

［2］ KESERLA A，PETERS 段 .Analysis of dual－shuttle automated storage／retrieval systems［J］.Journal of Manufacturing Systems，1994，13（6）：424－434.

［3］ MALMBORG 段 .Interleaving models for the analysis of twin shuttle automated storage and retrieval systems［J］.International Journal of Production Research，2000，38（18）：4599－4610.

［4］ AZZI A，BATTINI D，FACCIO M，et al.Innovative travel time model for dual－shuttle automated storage／retrieval systems［J］.Computers and Industrial Engineering，2011，61（3）：600－607.

［5］ MELLER 段 ，MUNGWATTANA A.Multi－shuttle automated storage／retrieval systems［J］.IIE Transactions，1997，29（10）：925－938.

［6］ LERHER T，SRAML M，POTRC I.Simulation analysis of mini－load multi－shuttle automated storage and retrieval systems［J］.The International Journal of Advanced Manufacturing Technology，2011，54（1／2／3／4）：337－348.

［7］ POTRC I，LERHER T，KRAMBERGER J，et al.Simulation model of multi－shuttle automated storage and retrieval systems［J］.Journal of Materials Processing Technology，2004，157／158（20）：236－244.

［8］ YANG Peng，MIAO Lixin，QI Mingyao.Slotting optimization in a multi－shuttle automated storage and retrieval system［J］.Computer Integrated Manufacturing Systems，2011，17（5）：1050－1055（in Chinese）.［杨 朋，缪立新，戚铭尧.多载具自动化存取系统货位分配优化［J］.计算机集成制造系统，2011，17（5）：1050－1055.］

［9］ YANG Peng，MIAO Lixin，QI Mingyao.Integrated optimization of storage location assignment and routing planning in a multi－shuttle automated storage and retrieval system［J］.Journal of Tsinghua University：Science and Technology，2011，51（2）：261－266（in Chinese）.［杨 朋，缪立新，戚铭尧.多载具自动化存取系统货位分配和拣选路径集成优化［J］.清华大学学报：自然科学版，2011，51（2）：261－266.］

［10］ GUO 段 ，LIU L U.An evaluation of storage assignment policies for twin shuttle AS／RS［C］／／Proceedings of 2010 IEEE International Conference on Management of Innovation and Technology.Washington，D.C.，USA：IEEE Computer Society，2010.

［11］ TANAKA S，ARAKI M.An exact algorithm for the input／output scheduling problem in an end－of－aisle multi－shuttle automated storage／retrieval system with dedicated storage［J］.Transactions of the Society of Instrument and Control Engineers，2006，42（9）：1058－1066.

［12］ TANAKA S.A hybrid algorithm for the input／output scheduling problem of multi－shuttle AS／RSs［C］／／Proceedings of the Society of Instrument and Control Engineers Society of Instrument and Control Engineers.Washington，D.C.，USA：IEEE，2007.

［13］ KUBOTA Y，NUMATA K.An exact algorithm based on Lagrangian relaxation for the input－output scheduling problem in automated warehouses［C］／／Proceedings of the ICCAS－SICE.Washington，D.C.，USA：IEEE，2009：753－758.

［14］ DOOLY 段 ，LEE L E.A shift－based sequencing method for twin－shuttle automated storage and retrieval systems［J］.IIE Transactions，2008，40（6）：586－594.

［15］ XIE Jinxing，XING Wenxun，WANG Zhenbo.Network optimization［M］.Beijing：Tsinghua University Press，2009（in Chinese）.［谢金星，刑文训，王振波.网络优化［M］.北京：清华大学出版社，2009.］.

［16］ RICHARD 段 .Reducibility among combinatorial problems［M］／／Complexity of Computations.New York，N.Y.，USA：Plenum，1972：85－103.