知识化制造系统产品工艺路线的自重构

万晓琴，严洪森

（1.东南大学 自动化学院，江苏 南京 210096；2.东南大学复杂工程系统测量与控制教育部重点实验室，江苏 南京 210096）

0 引言

知识化制造系统（Knowledgeable Manufacturing System，KMS）是于2000年提出的一种带有“六自”特征的新的制造理念［1］，致力于解决现有制造模式中存在的模式单一、缺乏灵活性、不能满足制造企业需求多样性及重复研发等问题。自重构是KMS重要的特征之一，也是现代制造系统中迫切需要的功能，其自重构包括KMS管理与控制软件的自重构［2］、硬件的重构两方面内容。

对制造系统的硬件进行重构已引起研究者越来越多的关注，其目的在于以低成本的重构方式快速改变系统的构形［3］。梁福军等［4］对可重构制造系统（Reconfigurable Manufacturing System，RMS）的结构、组成、类别及理论体系进行了研究。KATZR［5］研究了可重构机床（Reconfigurable Machine Tool，RMT）的设计原则，通过调整RMT的组成模块，快速实现机床结构的变化，达到转变加工任务的目的。文献［6－9］针对可重构零件族进行了深入研究，采用改变设备物理位置、增减设备的数量及更换设备上的加工模块等方法实现制造单元内硬件的物理重构，解决生产线零件族中各零件在确定或随机需求情况下的构形优化问题。文献［10］针对单件小批量生产提出面向多工序加工系统的分层可重构工艺规划体系构架，以非加工时间和相对时间偏差为目标，建立了可重构工艺规划的数学模型。文献［11］提出一种从加工序列、机床、刀具和切削参数等多个因素，对复杂零件工艺方案进行全局多层并行优化的方法。目前，对硬件重构的研究主要集中在制造系统的物理重构上，然而现有制造系统设备的位置大多被固定，想要移动设备并非易事。对于工艺规划可重构的研究大多针对当前产品特征及设备能力进行重构，是对制造系统进行首次构建，目前关于充分利用原生产线已有制造系统资源的重构研究还较少。

针对以上不足，本文对KMS多产品工艺路线逻辑重构问题进行数学建模。当产品数量和混合比发生变化时，在充分利用原生产线已有资源的基础上，适当调整产品的工艺加工路线，快速响应当前的生产需求。提出一种改进的混沌非支配排序遗传算法（Nondominated Sorting Genetic Algorithm，NSGA）优化各产品工艺加工路线，在对目标函数无偏好的情况下，为决策者提供多种可选工艺路径重构方案。

1 问题描述与模型建立

1.1 问题描述

KMS产品工艺路线重构问题可以描述为：知识化制造单元内有m台机器，所有缓冲区容量为无限大；可加工n种工件，各工件包含由多道工序组成的工序集，每道工序可在多台性能不同的机器上加工，工序的加工时间因机器性能不同而不同；受市场需求变化的影响，待加工的工件种类及数量发生变化，当原有生产线的生产能力已经不能满足现在市场需求时，对生产线进行逻辑重构，在充分利用已有资源的基础上，优化各产品工艺路线，使其满足生产需求且重构成本最低。

制造单元内需要加工多种工件，每种工件有多条可选工艺路线。现做如下假设：

（1）机器故障率为0。

（2）工件加工遵守先到先服务的调度规则。

（3）工件可在同一台机器上加工不同工序。

（4）每道工序可在多台性能不同的机器上加工。

（5）每一时刻每台机器只能加工一个工件。

（6）一个工件在同一时刻只能在一台机器上加工。

（7）工序的准备时间与顺序无关，包含在加工时间内。

（8）各工件的到达过程为泊松过程，服务时间服从负指数分布。

（9）原生产线包含了待加工工件的所有工序加工能力。

1.2 模型建立

1.2.1 输入信息

m为车间内的设备总数，设备编号为1，2，…，m，h＝1，2，…，m；

n为制造单元内待加工的工件种类总数，工件种类依次编号为1，2，…，n，p＝1，2，…，n；

k为知识化制造单元内可加工的所有工序的总数，所有可加工工序依次编号为1，2，…，k，x，y＝1，2，…，k；

J［1，…，n］为各工件包含的工序数目矩阵，J（p）即第p 类工件包含的工序数目，i，j＝1，…，J（p）；

Op［1，…，J（p）］为第p类工件包含的工序集；

Gp［1，…，J（p）］［1，…，J（p）］为第p类工件工序优先级矩阵；

由1.1节假设（7）可知：对于某类工件p，相继到达的两个第p类型工件之间的时间间隔为独立同分布的，服从参数为λp的负指数分布。第p类工件的第i道工序Op（i）若能在机器m上加工，则加工时间服从参数为τp，i，h的负指数分布。

1.2.2 原生产线描述

n0为原生产线加工的工件种类数，p0＝1，2，…，n0；

P0p0［1，…，J（p0）］为原生产线加工第p0类工件的工序序列，工序的加工先后顺序为P0p0（1），P0p0（2），…，P0p0（J（p0））；

M0p0［1，…，J（p0）］为原生产线第p0类工件工序加工对应的机器序列。

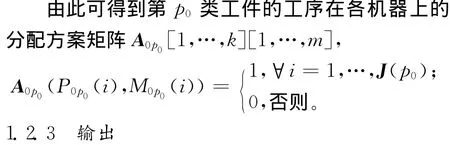
Pp［1，…，J（p）］为第p类工件工艺路线重构后的工序序列；

Mp［1，…，J（p）］为第p类工件工艺路线重构后工序加工对应的机器序列；

同上，可以得到第p类工件工艺路线重构后的工序在各机器上的分配方案矩阵：

Ap［1，…，k］［1，…，m］，

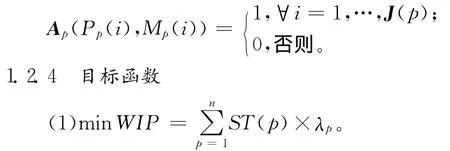
该目标函数是最小化平均在制品水平，本文假设各缓冲区的容量为无限大，生产线达到稳定情况下，产品的到达率等于生产率。在给定工件生产率的前提下，优化工件工艺路线，使各工件逗留时间ST（工件从进入制造系统到完成生产离开该系统所需要的时间）最短。本文利用文献［12－13］提出的排队网络分析方法，计算出工件在机器上的加工时间和等待时间，再加上工件在加工路线上的运输时间（假设运输时间与机器之间的距离成正比），最后计算出第p类工件的ST（p）由工件的加工时间、等待时间及运输时间三部分组成。由Little公式可知，生产线的平均在制品水平等于工件的逗留时间乘以到达率，其物理意义是最小化平均在制品数量。

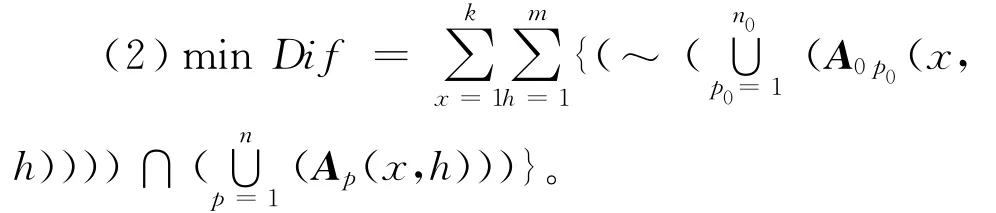
该目标是计算重构后的生产线与原生产线相比，机器加工与原来不同种类工序的总数目。三个符号∪，∩和～分别表示两矩阵对应位置元素间进行与、或、非逻辑运算。其物理意义是制造单元内重构前后相同机器加工不同工序时由工人熟练程度和更换刀具等带来的生产成本。

命题1 Dif为重构后的生产线与原生产线相比，相同机器加工与原来不同种类工序的数目总和。

证明 由1.2.2节和1.2.3节可知，A0p0，Ap均为k×m维0／1矩阵，当A0p0（x，h），Ap（x，h）值为1时，分别表示第p和p0类产品的编号为x的工序在编号为h的机器上进行加工，值为0时表示第p和p0类产品不包括编号为x的工序，或者编号为x的工序不在编号为h的机器上进行加工。令（A0p0），表示原生产线加工n0种工件时k种工序在m 种机器上的加工分配情况表示重构后生产线加工n种工件时k道工序在m台机器上的加工分配情况。A3＝｛～A1∩A2｝。

（1）A1（x，h）＝1，A2（x，h）＝1，表示原生产线和重构后的生产线，工序编号为x的工序均在机器编号为h的机器上加工，此时A3（x，h）＝0。

（2）A1（x，h）＝1，A2（x，h）＝0，表示原生产线编号为x的工序在编号为h的机器上加工，重构后编号为x的工序不在编号为h的机器上加工，此时A3（x，h）＝0。

（3）A1（x，h）＝0，A2（x，h）＝1，表示原生产线编号为x的工序不在编号为h的机器上加工，重构后编号为x的工序在编号为h的机器上加工，此时A3（x，h）＝1。

（4）A1（x，h）＝0，A2（x，h）＝0，表示原生产线和重构后的生产线，工序编号为x的工序均不在机器编号为h的机器上加工，此时A3（x，h）＝0。

对于上述四种情况，仅在情况（3）中，对于机器h，重构前不加工编号为x的工序，而重构后需对编号为x的工序进行加工，这种重构前后〈机器，工序〉的分配变化会增加生产成本（由工人熟练程度和更换刀具等带来的成本）。情况（2）中，对于重构后的生产线而言，机器h并未增添新的工序，不会增加成本，故不计入〈机器，工序〉的变动数目中。此目标等价于 min Dif ＝ ∑x，h｛A3（x，h）＝1｝，即重构前后〈机器，工序〉的分配变化数目的总和。证毕。

1.2.5 数学模型

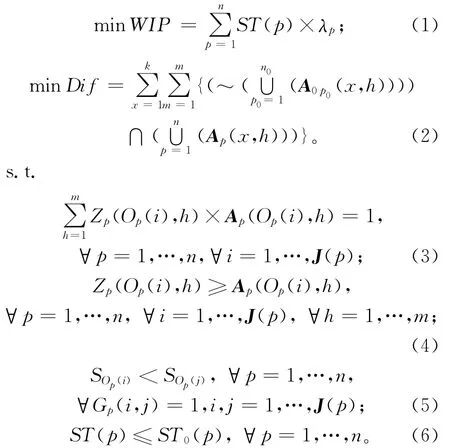
其中：式（3）为加工完整性约束，该约束保证每个工件的每道工序都能分配到某台机器上进行加工；式（4）是机器加工可行性约束，该约束保证各工序分配到的机器能进行此工序的加工；式（5）是工序优先约束，该约束保证工件的加工顺序满足工序优先约束，SOp（i），SOp（j）是工序Op（i），Op（j）在加工方案中的加工次序；式（6）是逗留时间约束，当生产率接近制造系统容量时，逗留时间会趋于无限大［14］，使生产线在制品水平剧增，因此将逗留时间约束在一定范围内，ST0（p）为第p类产品的最大逗留时间。

2 改进混沌非支配排序遗传算法

NSGA具有可对多个目标并行优化、能够同时获得多个Pareto最优解等特点，在多目标优化问题求解中得到越来越广泛的应用［15－16］。将混沌理论与NSGA相结合，利用混沌搜索技术较好的遍历性特点，有助于提高NSGA的局部搜索能力。目前混沌NSGA中的混沌映射主要基于Logistic映射和Tent映射。文献［17］在算法中加入混沌算子，用Logistic映射的混沌序列产生子代种群，文献［18－19］在NSGA的交叉变异算子的参数中引用Logistic映射，但由于Logistic映射遍历不均匀的特性会影响寻优的速度与结果。文献［20］在多目标遗传算法（Genetic Algorithm，GA）中引入改进Tent映射的自适应变尺度混沌优化方法，为了避免出现Tent映射迭代中陷入的小周期点和不动点，需要在每次映射迭代过程中循环检测小周期点和不动点。为此，本文采用Skew Tent映射［21］，提出一种改进混沌NSGA，使之具有较好的遍历均匀性，而且避免了计算机进行多次迭代后陷入小周期点和不动点。

2.1 编码与解码

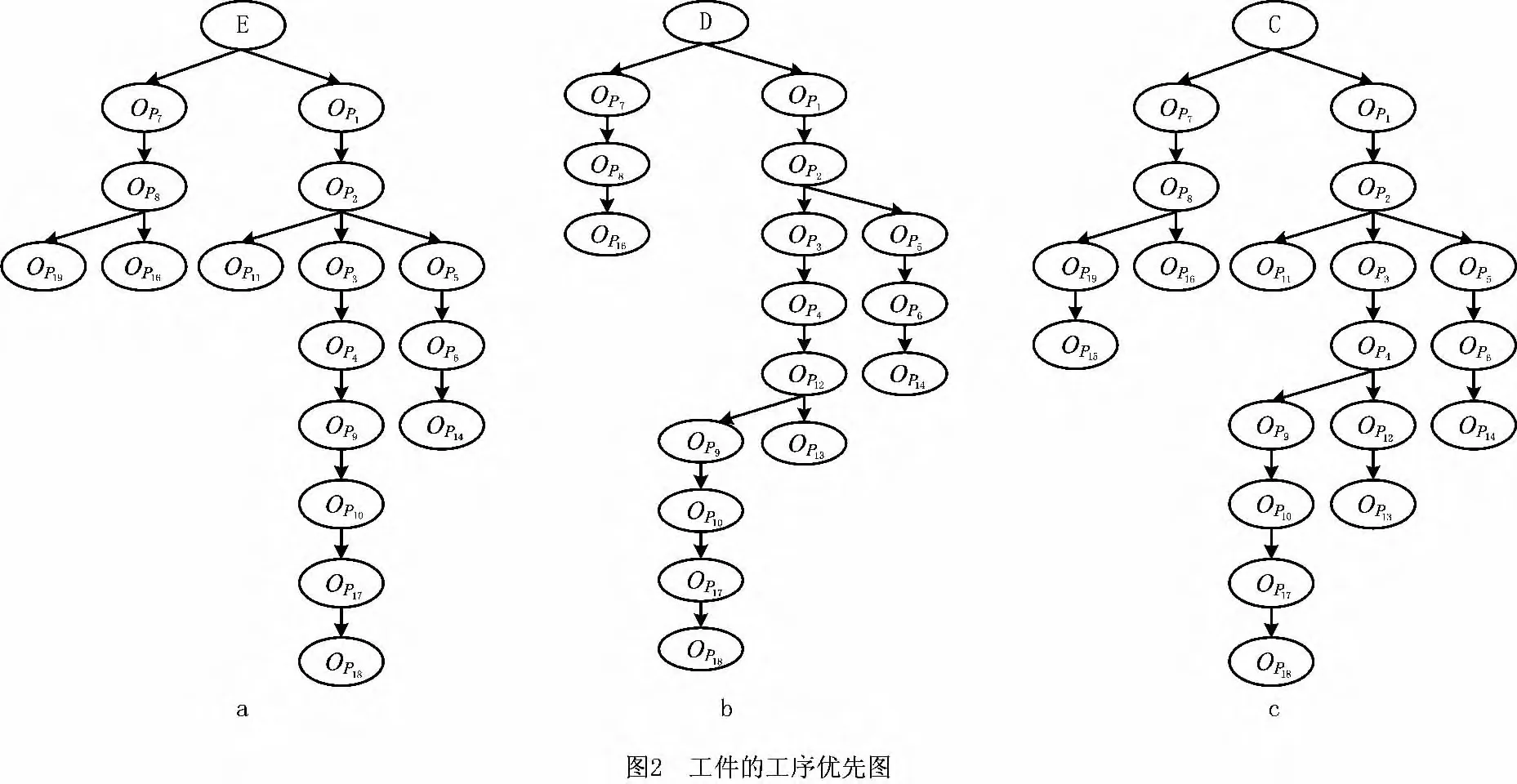
本文采用一种基于工序和机器的编码方式，染色体长度为所有待加工工件工序数目之和的两倍。前半段染色体采用基于工序优先权的编码方式［8，15］。染色体中基因的位置表示工件的各道工序，基因的值代表工序的优先权，优先权的任何改变通常导致不同的拓扑排序，这种编码方式本质上能够表示给定工序优先图的所有可行工序加工排序。染色体后半段（如图1中b）每个基因的值是在［1，m］之间的任意一个随机整数，其中m为车间的设备总数。在此编码的基础上，提出一种基于工序优先约束矩阵Gp和候选机器集的解码方法，以获得可行的产品加工工序序列及加工机器。下面以图2中的工件C为例说明染色体的编码与解码。

工件C包含19道工序，工序优先图如图2c所示，则染色体的前半段（如图1中a）每个基因的值是一个［1，19］之间唯一的整数值，构成了一个19个数的排列，数值越大表示相应基因位置代表的工序的优先权越高。

关于第p类工件工序加工序列解码如下：

根据1.2.1节中工件的Gp矩阵及染色体信息，可解码为一个可行的工件加工序列，算法如下：

步骤1 找出Gp矩阵中元素全为0的列i，…，j所对应工序Op（i），…，Op（j）在染色体中的优先权值。

步骤2 找出染色体优先权值中的最大值对应的工序列Op（l）并输出（l∈i，…，j），将染色体中此最大优先权值置0。

步骤3 将Gp矩阵的第l行置0。

步骤4 重复步骤1～ 步骤3共J（p）－1次，即可得到符合工序优先约束的工件加工工序序列。

第p类工件的工序对应的加工机器解码方法如下：令染色体后半段编码中OPi对应的基因的值为gi，候选机器总数为~ni，则

式中b的取值保证0＜~ki≤~ni即可，即选择候选机器的第~ki台机器加工工序OPi。

如图1b所示，工序OP1对应编码基因的值为6，机器与工序加工关系如表1所示，则工序OP1可由两种候选机器｛M3，M6｝进行加工。由~ki＝6－2×2＝2，OP1在两台候选机器中的第2台机器，即M6机器上加工，加工时间为8s。此方法解码得到的工序分配方案必定满足机器加工可行性约束。

表1 各道工序在机器上的加工时间s

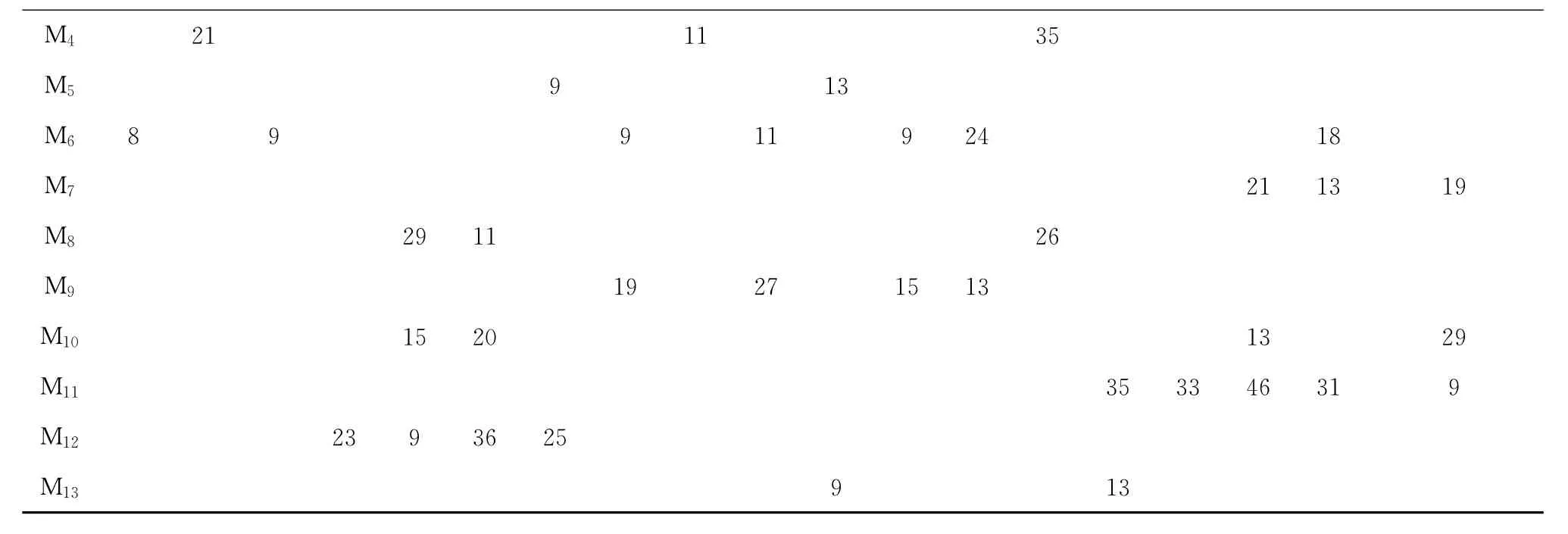
续表1

图1解码后，工件C的工序加工顺序及所选机器如图3所示。

图3中第一行为工序的加工顺序序列，第二行为对应于第一行的工序所选的加工机器序列。即工件C首先在机器M6上加工工序OP1，然后在机器M4上加工工序OP2，后面的工序及机器以此类推。

2.2 选择、交叉、变异算子及混沌扰动

（1）选择算子 轮盘赌选择方式，即根据每个染色体适应值的比例来确定该个体的选择概率。

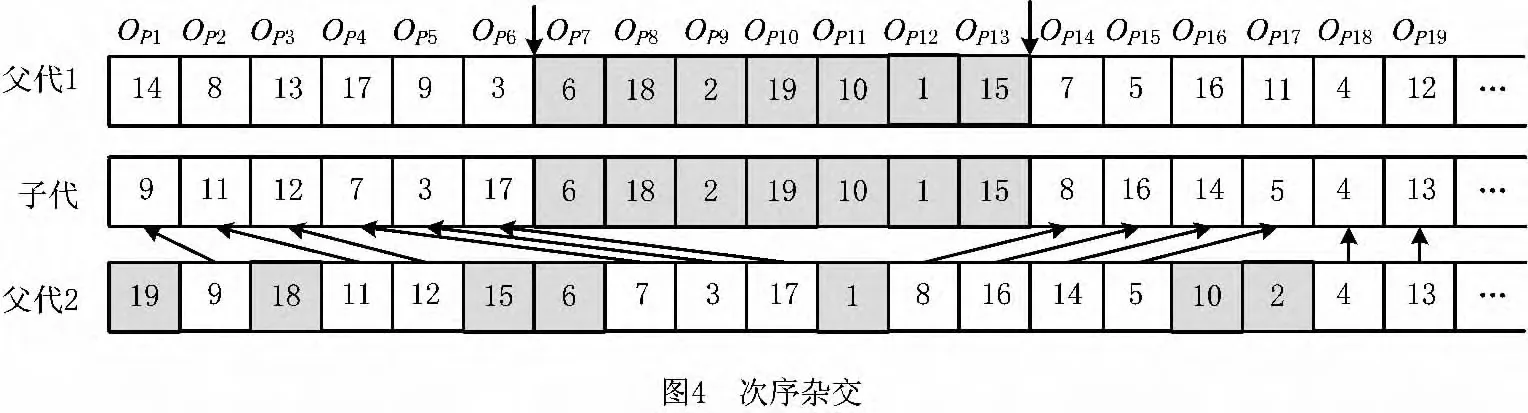
（2）交叉算子 前半段染色体采用次序杂交（order crossover）的方式［15］，杂交过程如图4所示。后半段染色体采用经典的部分匹配交叉，即交换父代交叉点之间的子串内容。

（3）变异算子 前半段和后半段染色体均采用交换变异，随机选择两个基因位置，然后交换它们的基因值。

（4）混沌扰动算子 斜帐篷映射［21］（Skew Tent）结构简单，具有较好的遍历均匀性。其数学表达式为

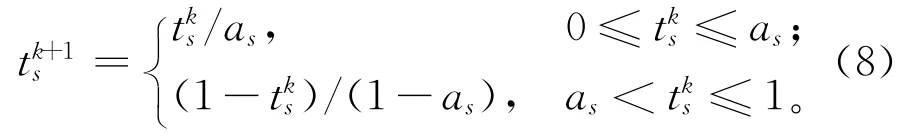
当as＝0.5时即为Tent映射。计算机在进行Tent映射时，实际上是将小数部分的二进制数进行无符号左移，又因为计算机字长有限，小数部分经过一定次数的左移运算将趋于0［22］，影响搜索结果。在改进的混沌扰动算子中取as∈ （0，0.5）∪ （0.5，1）。为避免染色体不同位置基因具有相同初值tks时，Skew Tent映射产生相同的搜索序列，在改进的混沌扰动算子中针对每一基因，对as赋以（0，0.5）∪ （0.5，1）区间内的随机值，再利用具有不同as参数的Skew Tent映射对染色体后半段进行局部扰动，即在工序加工顺序一定的情况下，对工序所属的机器进行重新搜索寻优。

改进的混沌扰动算子步骤如下：

步骤1 设置最大迭代次数K＊，记录个体的目标值WIP＊和Dif＊。令迭代步数初值k＊＝1，随机产生向量a＝［a1，…，as，…，aq］，as∈（0，0.5）∪（0.5，1）。

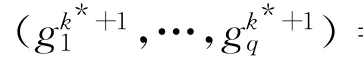
步骤5 k＊＋1→k＊，若k＊≤K＊，则转步骤2，否则算法结束。

2.3 适应值分配机制及Pareto解集过滤器

采用群体排序技术寻找Pareto最优解。根据遗传算法中个体的相互支配关系对个体进行分级，每一代的非支配解作为第1级点，剩下的个体所分配的级数等于支配该个体的数量加1。

定义1 群体分级后每个个体的适应度为

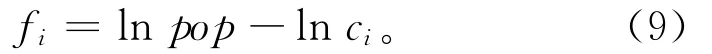
式中：fi为第i个个体的适应度，ci为群体中第i个个体的级数，pop为群体规模。由上式可以看出，相同等级的个体都具有相同的适应度，这样算法就不会只收敛到一点，而是收敛到一个非劣解集合。

Pareto解集过滤器存储每代产生的非劣解。在每一代中，过滤器中的解集通过加入新产生的Pareto解和删除所有支配解来更新。

规则1 当产品工艺路线重构后，该产品逗留时间大于最大逗留时间，即不满足式（6）时，适应值置0。

3 应用实例

某冲压车间内有19台机器，原生产线加工E和D两种工件，生产率分别为65件／h和22件／h。由于市场需求变化，现要求生产D和C两种工件，生产率要求分别为65件／h和25件／h。要求对产品工艺路线进行规划，使其满足生产率要求且重构成本最小。机器间的距离矩阵如表2所示，设备加工各工序的时间如表1所示。各工件的工序优先图如图2所示。原生产线信息如下：

工件E工序加工顺序为PE＝｛7，1，2，5，11，3，4，6，14，8，19，16，9，10，17，18｝；

工件D工序加工顺序为PD＝｛1，7，8，16，2，3，5，6，14，4，12，9，10，17，18，13｝；

工件E工序加工对应的机器为ME＝｛5，6，3，12，13，6，2，10，8，9，11，1，4，6，10，7｝；

工件D工序加工对应的机器为MD＝｛6，5，9，1，3，6，12，10，8，2，9，4，6，10，7，9｝。

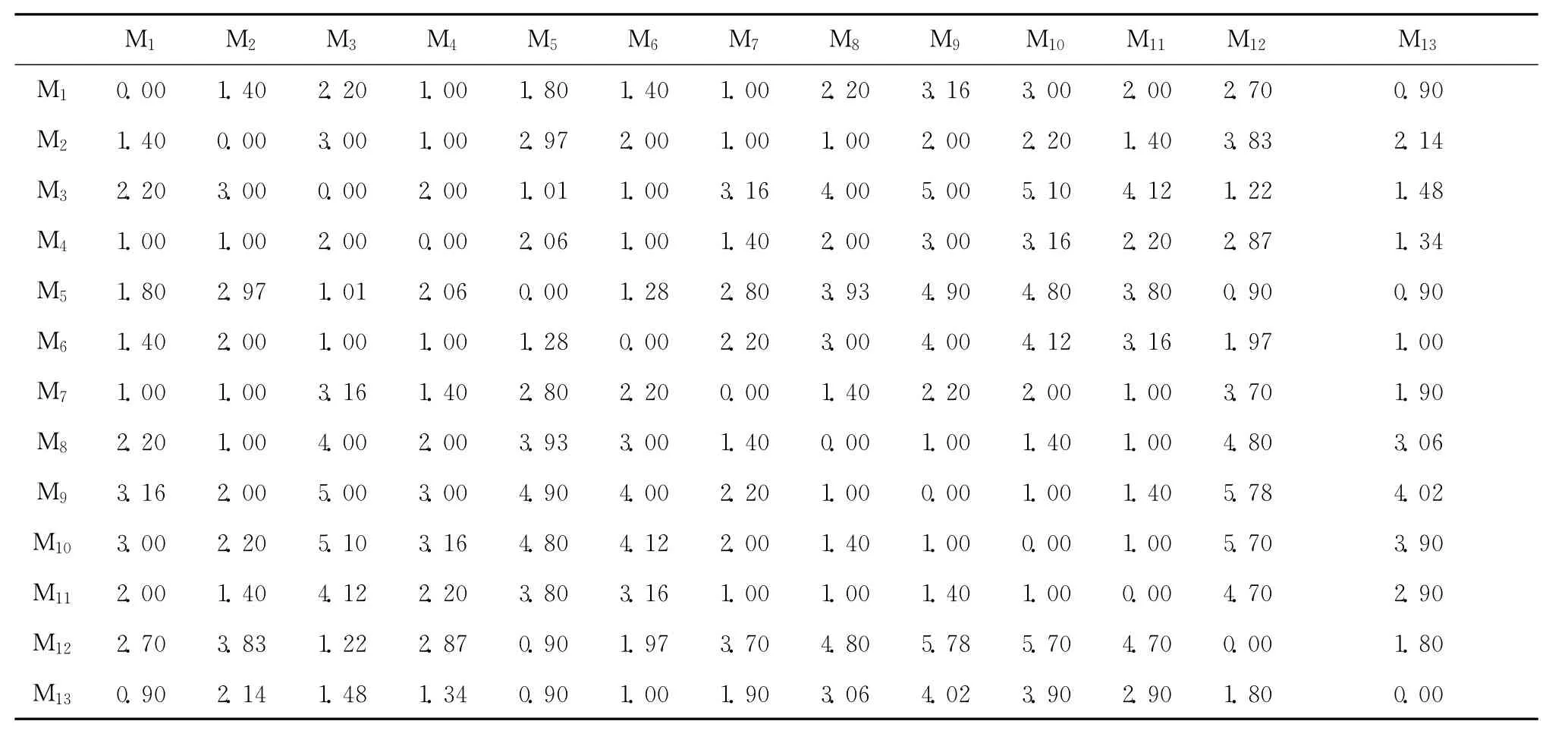
表2 制造单元内设备间距离矩阵m

所有程序在MATLAB平台上仿真运行，具体算法参数设置为：种群规模pop＝80，进化代数genmax＝500，交叉率pc＝0.9，变异率pm＝0.3，混沌迭代次数K＊＝300。在不同生产率需求条件下，针对工件D的工艺路线重构和不重构两种情况，对制造系统的性能进行比较分析。采用C－NSGA解决多目标优化问题，经过多次独立运行，得到Pareto最优解分布图如图5所示。图中WIP（单位：个）为生产线中的平均在制品数量，为优化目标中的第一个目标值；Dif（单位：个）为重构后的生产线与原生产线相比，相同机器加工与原来不同种类工序的数目总和，为第二个优化目标值。在生产率需求较小的情况下（如图5a），当Dif值相同时，重构后生产线的平均在制品数量略少，此时生产线可以不进行逻辑重构。当生产率需求增加时，工件D的工艺路线重构和不重构两种情况下，生产系统WIP数量差别越来越大，如图5b所示。当工件D和C的需求率分别为68件／h和29件／h时，若D工件工艺路线不重构，则生产线的WIP数量达到50，如图5c所示。这两种情况可认为生产线已不满足需求，必须进行逻辑重构。表3列出了图5b中工艺路线重构的7种方案，各方案对应的产品工艺加工路线如表4所示。

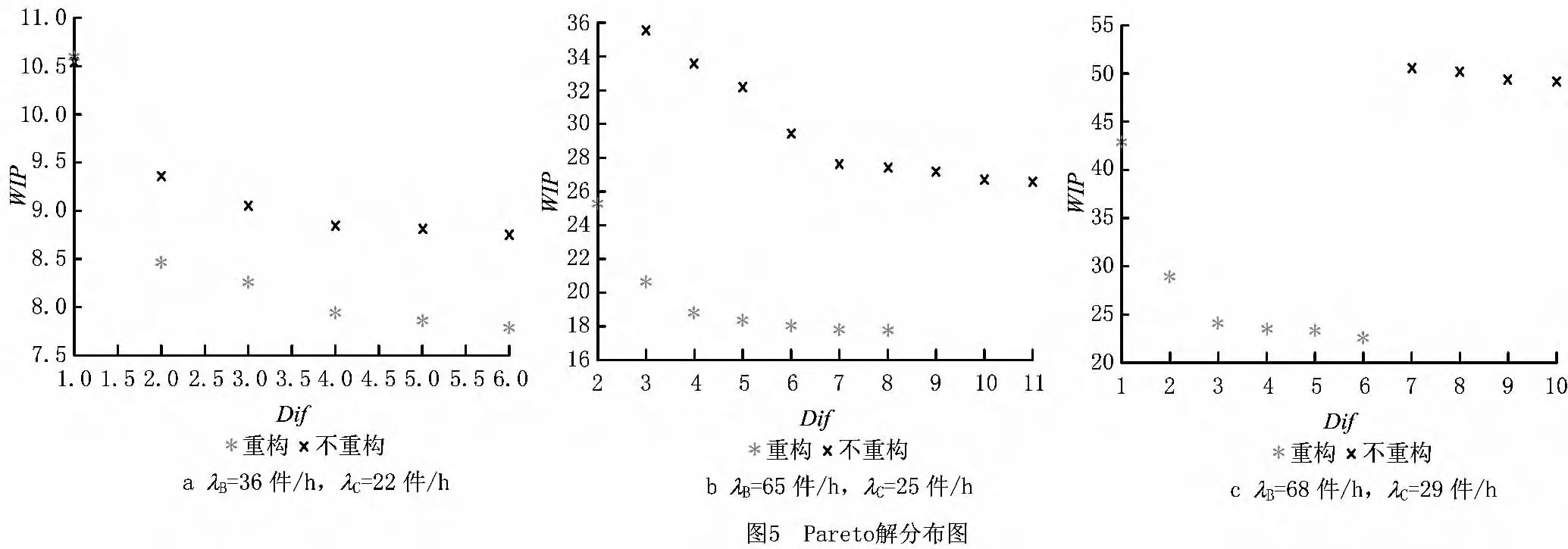
表3 重构方案

表4 重构后的产品加工工艺路线

续表4

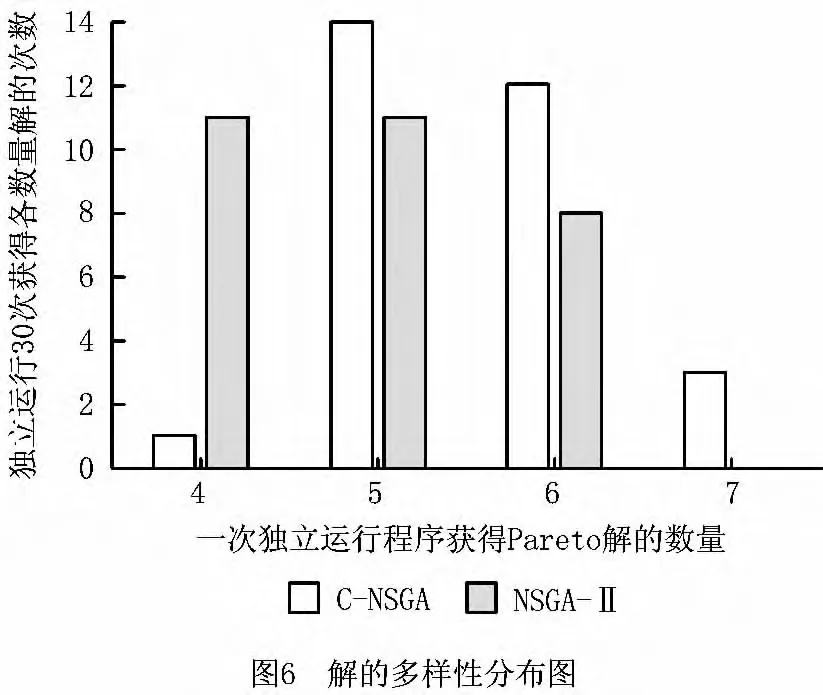
NSGA－Ⅱ［23］是求解多目标问题的一种比较成熟的算法。下面比较C－NSGA和NSGA－Ⅱ在Pareto解的取值和解的个数两方面的性能。在λB＝65件／h和λC＝25件／h情况下，独立运行C－NSGA和NSGA－Ⅱ程序各30次。

比较分析结果如下：

从表5和图6可以看出，与NSGA－Ⅱ相比，CNSGA在解的多样性上表现较优，一般能得到5或6个非支配解。在Dif值相同时，C－NSGA能得到更小的WIP值，且最大值与最小值的差距较小，解的稳定性更好。

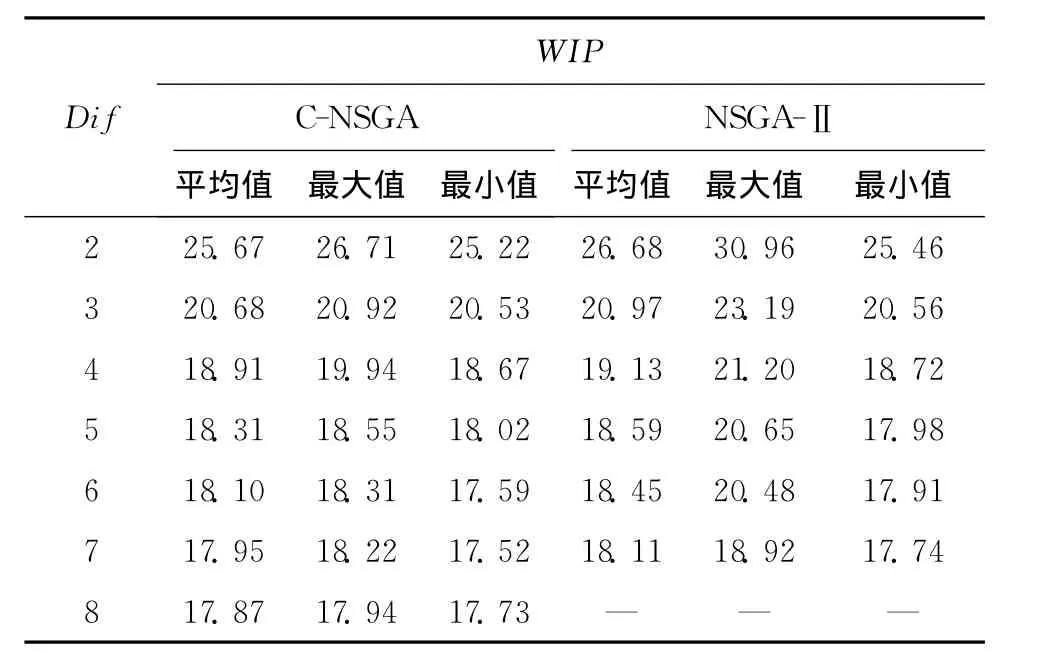
表5 C－NSGA和NSGA－Ⅱ运行情况对照表

从图5可以看出，优化的两个目标之间存在矛盾，当WIP数目减少时，Dif的数目增加，反之亦然。在不同生产率需求下，重构后生产线的性能更优；生产率越高，重构的优势越能体现。Pareto解集列出了两目标函数解空间内可能的最优解，从而增加了决策者可选择的空间，最终两个目标函数间如何平衡，由决策者根据经验确定。表4给出了各种重构方案对应的产品加工工艺路线，在决策者根据各个目标函数的相对重要性确定了目标函数值后，就可以从表4中找到与其对应的产品重构后的工艺路线。

4 结束语

本文对知识化制造环境下的多产品工艺路径规划问题进行了研究，在不考虑各目标函数间权重分配的情况下，对两个相互冲突的目标函数进行并行优化，得到一组Pareto可行解。决策者可以根据不同企业对目标的不同偏好，从候选解集中选出最符合要求的重构方案。当工件的种类和需求数量发生变化时，在充分利用原有资源的基础上，KMS能够做出快速响应，很快形成一条新的生产线。需要指出的是，文本目前只考虑了工艺路线的逻辑重构，在实际生产中，有些情况下的工艺由生产线上的机器决定，例如，在新加入的零件工艺中，当含有原系统不能完成的工序，或者相关工序的可用机器集内的机器指派调整受限，或者产品需求大大超过生产线最大生产能力时，仅进行工艺路线的重构无法满足生产能力的提升，需要对机器种类和数量进行更换，同时考虑工艺路线重构和机器重构（即物理重构）将作为进一步研究的内容。

［1］ YAN Hongsen，LIU Fei.Knowledgeable manufacturing system—a new kind of advanced manufacturing system［J］.Computer Integrated Manufacturing Systems，2001，7（8）：7－11（in Chinese）.［严洪森，刘 飞.知识化制造系统——新一代先进制造系统［J］.计算机集成制造系统，2001，7（8）：7－11.］

［2］ XUE Chaogai.Research into the self－reconfiguration of knowledgeable manufacturing system［D］.Nanjing：Southeast Uni－versity，2005（in Chinese）.［薛朝改.知识化制造系统的自重构研究［D］.南京：东南大学，2005.］

［3］ KOREN Y，HEISEL U，JOVANE F，et a1.Reconfigurable manufacturing system［J］.CIRP Annals，1999，48（2）：527－540.

［4］ LIANG Fujun，NING Ruxin.Theoretical research of reconfigurable manufacturing system［J］.Chinese Journal of Mechanical Engineering，2003，39（6）：36－43（in Chinese）.［梁福军，宁汝新.可重构制造系统理论研究［J］.机械工程学报，2003，39（6）：36－43.］

［5］ KATZ R.Design principles of reconfigurable machines［J］.International Journal of Advanced Manufacturing Technology，2007，34（5）：430－439.

［6］ SON 段 .Design principles and methodologies for reconfigurable machining systems［D］.Ann Arbor，Mich.，USA：University of Michigan，2000.

［7］ YOUSSEF 段 A，EIMARAGHYH A.Availability consideration in the optimal selection of multiple－aspect RMS configurations［J］.International Journal of Production Research，2008，46（21）：5849－5882.

［8］ DOU Jianping，DAI Xianzhong，LI Jun.Optimization for multi－part flow－line configurations of reconfigurable manufacturing systems based on genetic algorithm［J］.Computer Integrated Manufacturing Systems，2010，16（7）：1390－1400（in Chinese）.［窦建平，戴先中，李 俊.基于遗传算法的可重构制造系统多零件流水线构形优化［J］.计算机集成制造系统，2010，16（7）：1390－1400.］

［9］ LOU Hongliang，YANG Jiangxin，LIN Yafu，et al.Reconfigurating policy of reconfigurable manufacturing systems based on graph theory［J］.Chinese Journal of Mechanical Engineering，2006，42（3）：22－29（in Chinese）.［楼洪梁，杨将新，林亚福，等.基于图论的可重构制造系统重构策略［J］.机械工程学报，2006，42（3）：22－29.］

［10］ DUAN Jianguo，LI Aiping，XIE Nan，et al.Reconfigurable process planning for multi－stage machining systems［J］.Computer Integrated Manufacturing Systems，2011，17（6）：1215－1223（in Chinese）.［段建国，李爱平，谢 楠，等.面向多工序加工系统的可重构工艺规划［J］.计算机集成制造系统，2011，17（6）：1215－1223.］

［11］ CAI Ligang，ZHANG Jianshe，ZHANG Zhengyi，et al.Global multilayer and parallel process optimization of complex components［J］.Chinese Journal of Mechanical Engineering，2008，44（9）：6－12（in Chinese）.［蔡立刚，张建设，张正义，等.复杂零件工艺方案全局多层并行优化［J］.机械工程学报，2008，44（9）：6－12.］

［12］ SEGAL M，WHITT W.A queueing network analyzer for manufacturing［C］／／Proceedings of the 12th International Teletraffic Conference.Amsterdam，the Netherlands：Elsevier，1989，2：1146－1152.

［13］ WHITT W.The queueing network analyzer［J］.Bell System Technology Journal，1983，62（9）：2779－2815.

［14］ WEIN 段 .On the relationship between yield and cycle time in semiconductor wafer fabrication［J］.IEEE Transaction on Semiconductor Manufacturing，1992，5（2）：156－158.

［15］ GEN M，CHENGR W.Genetic algorithms and engineering optimization［M］.New York，N.Y.，USA：John Wiley ＆Sons，2000.

［16］ CHENG 段 ，DAN Li.Multiobjective optimization design with Pareto genetic algorithm ［J］.Journal of Structural Engineering，1997，123（9）：1252－1261.

［17］ WANG Junping，HUANG Jun，HAN Renmin，et al.Chaotic－NSGA－Ⅱ：an effective algorithm to solve multi－objective optimization problems［C］／／Proceedings of the International Conference on Intelligent Computing and Integrated Systems.Washington，D.C.，USA：IEEE，2010：20－23.

［18］ LU Hui，NIU Ruiyao，LIU Jing，et al.Multicriteria decision mechanism CNSGA－AHP for the automatic test task scheduling problem［J］.Information Technology Journal，2012，11（10）：1449－1455.

［19］ PAN I，DAS A.Chaotic multi－objective optimization based design of fractional order PIλDμcontroller in AVR system［J］.Electrical Power and Energy Systems，2012，43（1）：393－407.

［20］ WANG Ruiqi，ZHANG Chenghui，LI Ke.Multi－objective genetic algorithm based on improved chaotic optimization［J］.Control and Decision，2011，26（9）：1391－1397（in Chinese）.［王瑞琪，张承慧，李 珂.基于改进混沌优化的多目标遗传算法［J］.控制与决策，2011，26（9）：1391－1397.］

［21］ HASLER M，MAISTRENKO 段 .An introduction to the synchronization of chaotic systems：coupled skew tent maps［J］.IEEE Transactions on Circuits and SystemsⅠ：Fundamental Theory and Applications，1997，44（10）：856－866.

［22］ SHAN Liang，QIANG Hao，LI Jun，et al.Chaotic optimization algorithm based on Tent map［J］.Control and Decision，2012，20（2）：179－182（in Chinese）.［单 梁，强 浩，李军，等.基于Tent映射的混沌优化算法［J］.控制与决策，2012，20（2）：179－182.］

［23］ DEB K，PRATAP A，AGARWAL S，et al.A fast and elitist multiobjective genetic algorithm：NSGA－Ⅱ［J］.IEEE Transactions on Evolutionary Computation，2002，6（2）：182－197.