基于Delaunay细分的旋转对称模型最优对称单元的构造

曹伟娟，李 明，高曙明

（浙江大学CAD＆CG国家重点实验室，浙江 杭州 310027）

1 问题的提出

自然界和人造物体中存在很多旋转对称结构。在对具有旋转对称结构的模型进行有限元分析时，通常只取模型的一个对称单元来提高计算效率和分析精度［1］。但是，对同一个模型来说，对称单元的选择并不唯一，由不同形状的对称单元生成的有限元网格的质量及规模也不同。图1所示为同一零件的两个不同对称单元，图1c所示的对称单元与图1b所示的对称单元相比，网格节点数减少了约36%。在实际的工程应用中，分析人员一般通过在计算机辅助设计（Computer Aided Design，CAD）软件中手工构造分割面直接对原始模型进行分割的方式得到对称单元。手工构造对称单元主要有两个困难：①难以确定最终生成的网格的质量以及规模是否最优；②难以构造形状复杂的分割面。目前，自动构造对称单元方面的研究相对较少，且只能保证局部最优，效率也较低。虽然对称单元的形状决定了网格可能达到的质量和规模，但是目前还无法显式地表示二者之间的关系，很难通过直接比较形状来确定对称单元的好坏。另外，因为这种先分割再生成网格的方法会引入多余的固定边界，所以难免引入多余的网格节点。

针对以上问题，本文提出一种构造旋转对称模型最优对称单元的方法，选取输入模型的Delaunay三角网格的某个对称单元作为初始局部网格，通过对初始局部网格执行带对称约束的局部Delaunay细分算法，得到一个满足质量要求且规模最优的局部网格，该局部网格即输入模型的最优对称单元。方法生成的局部网格可以直接作为有限元分析的输入。与经典Delaunay细分算法相比，该方法仅对局部网格进行细分，因此效率较高。本文对所得对称单元的最优性进行了论证。

2 相关工作

本文相关工作包括对称单元的自动构造和基于Delaunay细分的网格生成两部分内容。

Suresh［2］在其关于对称性在工程分析中的自动应用研究中提出一种自动构造对称单元的方法，该方法利用某些启发式规则先筛选出一组对称单元作为候选，再从中选择生成网格质量最好的一个。这些启发式规则筛选对称单元的条件主要有：①对称边界到凹点的距离最远；②对称边界经过凹点等。这种启发式规则只能得到局部最优的对称单元，而且候选对称单元间的比较也较耗时。

由于Delaunay三角剖分具有一些很好的几何特性且简单易实现，成为目前最流行的通用的全自动网格生成方法之一［3］。Ruppert［4］提出的 Delaunay细分算法能够生成满足给定尺寸比的高质量三角网格，并从理论上保证网格规模不超过最优网格的常数倍。该方法通过不断在初始Delaunay三角网格中添加细分点来恢复边界和提高三角形质量，直到所有三角形都满足给定尺寸比。细分点主要添加在被侵入边界边（以该边为直径的圆包含其他节点）的中点以及狭长三角形的外接圆圆心。Ungor［5］给出另一种叫做偏置圆心的新的细分点，该细分点能够生成节点数更少、网格规模更小的三角网格。Zeng［6］在曲面重网格化研究中提出一种保对称的Delaunay三角化方法，通过添加一组对称的细分点来保证网格的对称性。目前大部分网格化方法都难以保证对称模型网格的对称性，主要原因有数值误差导致节点不对称、退化情况的Delaunay三角化导致三角形的不对称等。虽然Zeng通过添加对称的细分点解除了数值误差的影响，但仍无法避免退化的Delaunay三角形引起的不对称。

3 方法概述

对有限元分析来说，生成网格质量越高、网格数量越少的对称单元越好。理论上，如果模型是对称的，则生成的网格也应是对称的，最优对称网格的对称单元即为模型的最优对称单元。但是通过构造整体模型的对称网格来确定对称单元显然不合实际，因为整体划分代价较高，而且现有的网格划分方法无法保证网格的对称性。直接分割模型区域的方法无法保证网格的最优性，由于引入了新的边界，势必增加多余的网格节点，而且会使原有模型的局部特征尺寸变小，网格规模进一步增大。

鉴于Delaunay细分算法对网格质量和规模的理论保证，本文提出通过基于Delaunay细分的网格划分方法构造最优对称单元，其基本思想是：通过带对称约束的局部Delaunay细分构造输入模型最优对称网格的对称单元，细分过程中通过对称操作维护局部网格的Delaunay性质以及对称边界间的对应关系。

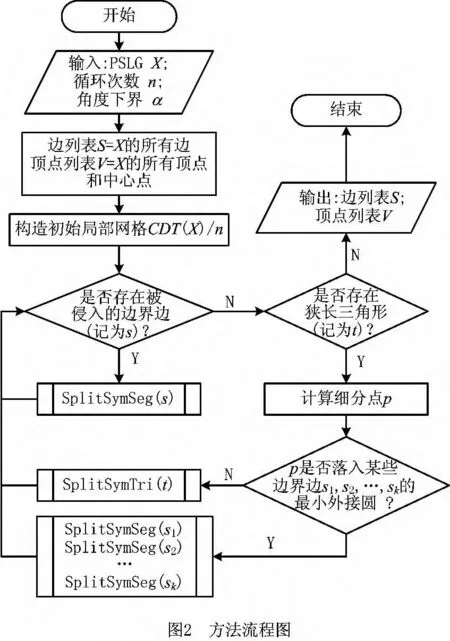
方法的输入是由平面直线图（Planar Straight－Line Graph，PSLG）表示的二维旋转对称区域，并假定对称阶数已知，记为n；方法的输出为由一组三角网格表示的最优对称单元。最优的含义指在给定网格质量前提下，网格规模不超过最小对称单元网格的常数倍。评价网格质量的标准为三角形角度值的下界，角度下界越小，网格质量越差；角度下界越大，网格规模越大。给定角度下界，可以预估所得网格的规模。方法流程如图2所示，基本过程与经典Delaunay细分算法类似，主要有三点不同：①细分的对象不是整个Delaunay三角网格，而是它的一个对称单元，即1／n局部网格；②细分点位置的确定；③添加新点后，通过带对称约束的边翻转操作更新Delaunay网格。下一章将分别针对这三点进行详细阐述。

4 带对称约束的局部Delaunay细分

4.1 初始局部网格的生成

初始网格的选取遵循以下原则：①初始网格必须是模型的一个对称单元网格；②初始网格必须是Delaunay网格。因为经典的Delaunay细分算法以模型的约束Delaunay三角割分（Constrained Delaunay Triangulation，CDT）作为初始网格，所以本文选取该网格的对称单元作为初始局部网格，以保证细分得到的对称单元网格具有同样的最优性。模型CDT的不同对称单元具有相同的单元数，节点数因对称边界的不同而稍有差异，但对最终结果的影响不大，所得对称单元网格都是最优的。本文选择对称边数目最少的对称单元作为初始局部网格，因为这样的网格节点数最少，并且需要移动三角形的次数通常也较少。其他的满足Delaunay属性的对称单元网格不可能具有更少的节点数，这些多余的节点位置不一定是最合适的，而Delaunay细分只能增加节点，不能删除节点，因此难以保证结果的最优性。

由于输入模型是对称的，其CDT也是对称的，可以找到一条由Delaunay边连接而成的路径，这条路径和由它绕中心点旋转360／n°得到的对称路径，以及模型的边界所界定的网格，就是初始局部网格。这条路径的末端节点分别属于模型的外环和中心环（或中心点）。为避免退化Delaunay三角形引起的歧义，计算相关节点在以对称中心为原点的极坐标系下的坐标，根据边长和节点的极坐标确定唯一的三角剖分。

生成初始局部网格的步骤如下：①生成模型的CDT；②计算各节点到其他所有节点的最短路径；③找出中心环节点和外环节点之间所有路径中最短的一条，以及与其对称的另一条路径，标记两路径上的边为对称边界，并关联相应的对称边；④移除对称边界外的所有网格。

为快速确定CDT中边的对称边，将所有对称节点组织为环状结构（如图3b），将环号和环内编号作为各点的索引，环号从内到外依次增大，环内节点按逆时针方向编号。若某节点所在环的长度为l，编号为i，则可以确定其对称点的编号为i＋l／n。

4.2 细分点位置的确定

如果网格中存在狭长三角形，则需要通过添加细分点来改善网格质量。记狭长三角形的外接圆圆心为o，则细分点的位置有四种情况：①当o位于局部网格内部时，为o；②当o位于模型区域外部或边界边上时，为距其最近的边界边的中点；③当o位于局部网格外部，但其某个对称点落在局部网格内部时，为该对称点；④当o位于对称边界上时，为o及其位于另一对称边界上的对称点。前两种情况下细分点位置的确定与经典Delaunay细分算法相同。后两种情况的判别和处理如下：在定位o所在的三角形时，如果o落在某条对称边界边的外侧，则找到与该边关连的另一条对称边界边，绕中心点将o向该对称边旋转360／n°得到o′，以o′代替o作为新的细分点，从对称边所在的三角形重新开始定位o′所在的三角形（如图4）；如果o落在某条对称边界边上，则通过旋转将其对称边所在的三角形移动到该边上（或将该边所在的三角形移动到其对称边上），并更新对称边界。

4.3 Delaunay网格的更新

加入细分点后分裂细分点所在的三角形，并通过边翻转更新Delaunay网格。如果待翻转边为对称边界边，则通过旋转将其对称边所在的三角形移动到待翻转边上（或将待翻转边所在的三角形移动到其对称边上），并对移动后的三角形执行翻转操作（如图5）。

在细分过程中，局部网格的对称边界在不断变化，最终的对称边界可能不是最短的。为减少最终网格节点数，在细分结束后，通过最短路径算法重新确定对称边界（如图6）。

4.4 曲线边界的处理

对于边界为曲线的输入模型，有两种处理方法：①先对曲线进行离散，以直线段取代曲线，再进行细分；②采用能够处理曲线边界的细分算法［7］。先离散再细分生成的网格与输入模型边界的拟合度取决于离散的质量，而且网格规模也会受到影响。本文目前采用第一种方法。

5 最优性证明

假设网格的角度下界为α。令θ＝360°／n，输入模型X 的对称群为Cn＝｛R0，R1，…，Rn－1｝，其中Ri（i∈N，0≤i＜n）为绕中心点逆时针旋转i×θ角度的对称变换。记局部细分算法生成的局部网格为LM，按照以下规则，通过整体细分向输入模型的CDT中添加细分点构造整体网格M：局部细分每添加一个细分点p，整体细分便添加n个p在Cn下的对称点qi＝Ri（p）（i∈N，0≤i＜n）。称由狭长三角形引入的细分点为内部细分点，由被侵入边界边引入的细分点为边界细分点，狭长三角形的外接圆和以被侵入边界边为直径的圆为细分点的空域圆。

以下应用［4］的框架证明M 是规模最优的，且LM＝M／n，因此LM也是规模最优的。给定PSLG X，可以定义X所在平面上任意一点的局部特征尺寸lfs为以该点为圆心且与X的两个边界实体（边或顶点）相交的最小圆的半径［4］，如图7所示。该函数满足Lipschitz条件，即对X所在平面上的任意两点p和q，有lfs（q）≤lfs（p）＋｜pq｜。

定理1 LM＝M／n。

证明 采用归纳法证明。

（1）记初始局部网格为LM0，初始整体网格为M0，根据初始局部网格的构造方法，有LM0＝M0／n。

（2）令第i次细分得到的局部网格为LMi，第i次整体细分得到的整体网格为Mi，如果LMi＝Mi／n，则LMi＋1＝Mi＋1／n。

令M′＝R0（LMi＋1）∪R1（LMi＋1）∪…∪Rn（LMi＋1）。首先，根据整体细分的加点规则，M′的节点与Mi＋1的节点相同。其次，M′中位于Ri（LMi＋1）内部的边都是局部Delaunay边，而根据局部细分中对边界边翻转的处理可知，Ri（LMi＋1）之间的对称边界边也是局部Delaunay边，因此M′的所有边都是Delaunay边，从而M′＝Mi＋1，LMi＋1＝Mi＋1／n。

（3）当局部细分结束时，整体细分也结束，根据归纳法，定理1成立。

引理1 令p和q为某次细分时加入的n个对称细分点中的两个相邻点，记p的空域圆半径为r，如果｜pq｜＜r，则必有θ＜60°，且｜pq｜＞2rsin（θ／2）。

证明 图8中的两个实心圆分别为p和q的空域圆，根据整体细分的对称性可知两圆全等，半径均为r，线段op和oq间的夹角为θ。根据Delaunay三角形的空外接圆性质，中心点o不可能落在两实心圆内部，因此有β≥θ。当｜pq｜＜r时，两圆相互包含对方圆心，｜pq｜＝2rsin（β／2）≥2rsin（θ／2）。解不等式r＞2rsin（θ／2），得θ＜60°。

引理2 存在常数CT和CS，使得以下结论成立：

（1）在尚未加入细分点时，每个输入节点p到其最近邻接点的距离至少为lfs（p）。

（2）当加入内部细分点p及其对称点时，p到其最近节点的距离至少为lfs（p）／CT。

（3）当加入边界细分点p及其对称点时，p到其最近邻接点的距离至少为lfs（p）／CS。

证明 根据局部特征尺寸的定义，结论（1）自然成立。根据引理1，当θ≥60°时，细分点p的最近节点永远是引入p的狭长三角形的节点或被侵入边界边的端点，根据文献［4］中的推导，引理2成立。当θ＜60°时，p的最近节点可能是其相邻对称点q。下面证明θ＜60°时引理也成立。

结论（2）：p为狭长三角形T的外接圆圆心，T的外接圆半径为r。按照文献［4］中引理2结论1的推导，当CS≥CT≥1时，有r≥lfs（p）／（1＋2CSsinα）。当｜pq｜≥r时，p的最近点为T的节点，距离为r；当｜pq｜＜r时，p的最近点为q，距离为｜pq｜。根据引理1，｜pq｜＞2rsin（θ／2）≥2sin（θ／2）lfs（p）／（1＋2CSsinα）。因此，当CT≥（1＋2CSsin α）／（2sin（θ／2））时，结论（2）成立。

结论（3）：p为被侵入边界边S的中点，S的长度为2r。按照文献［4］中引理2对情况2的推导，当CS≥1＋20.5CT时，有r≥lfs（p）／（1＋20.5＋21.5CSsinα）。当｜pq｜≥r时，p的最近点为S的端点，距离为r；当｜pq｜＜r时，p的最近点为q，距离为｜pq｜。根据引理1，｜pq｜＞2rsin（θ／2）≥2sin（θ／2）lfs（p）／（1＋20.5＋21.5CSsinα）。因此，当CS≥（1＋20.5＋21.5CSsinα）／（2sin（θ／2））时，结论（3）成立。

当sinα＜20.5sin（θ／2）／2时，选择CS＝ （1＋20.5）／（2sin（θ／2）－21.5sinα），CT＝ （1＋2CSsinα）／（2sin（θ／2）），可以同时满足方框中的条件。

引理3 M中任意节点p到其最近邻居q的距离不小于lfs（p）／（CS＋1）。

证明 如果p在q之后被加入或两者同时被加入，则根据引理2有｜pq｜≥lfs（p）／CS。如果p在节点q之前加入网格，则有｜pq｜≥lfs（q）／CS，根据Lipschitiz条件，｜pq｜≥（lfs（p）－｜pq｜）／CS，因此，｜pq｜≥lfs（p）／（CS＋1）。

定理2 M是规模最优的。

证明 根据文献［4］的论证，如果三角形半径边长比下限为A的网格M中任意节点p到其最近邻居的距离不小于lfs（p）／（CS＋1），则M 的规模不超过输入模型Ω的任一三角形半径边长比下限为A 的网格规模的C倍，其中C＝O（（CS＋1）2A）。因此，M是规模最优的。

定理3 LM是规模最优的。

证明 由定理1和定理2可得LM是规模最优的。

6 实现与结果

本文方法的实现基于开源程序Triangle［8］。对称边界上的边与其他边界边一样表示为边界子段，利用子段的标记属性来识别和区分中心环、外环和其他边界边。对称边界上的对应子段通过指针相互关联。因此，方法的核心是对称边界的处理，适用于任何基于Delaunay细分的网格划分算法，而不依赖于具体的细分算法，也可基于其他Delaunay细分算法来实现。

图9所示为若干二维模型的整体网格和两种对称单元网格的比较，角度下界为30°。第一列为对整体模型应用经典网格划分算法生成的网格；第二列为对直接分割得到的对称单元应用经典网格划分算法生成的网格，分割线为输入模型的CDT边；第三列为由本文方法基于细分构造的对称单元网格。图后的数字表示网格节点数。两组对称单元网格的规模相差不大，主要原因有：①选择CDT边作为分割线，使得基于细分的初始局部网格与基于直接分割的初始局部网格相同；②细分过程中对称边界的变化不大，因此对内部网格的影响也很小。由于二维模型形状相对简单，两种对称单元网格规模差别不明显，但是对三维模型，其对称单元的分割边界可能会很复杂，这种差别将会更为显著。

7 结束语

本文提出一种基于Delaunay细分构造旋转对称模型的最优对称单元的方法，该方法具有以下特点：①能够从理论上保证对称单元的最优性；②无需对原始模型进行分割和比较，且仅对局部网格进行细分，因此效率更高；③生成的对称单元网格可以直接作为有限元分析的输入。

未来工作主要有以下几点：①方法在三维情形的实现；②改进对曲线边界模型的处理；③考虑采用其他单元类型的最优对称单元的构造方法。本文方法主要面向三角形和四面体网格。对四边形或其他单元类型，目前并没有保证网格规模的理论依据，因此，本文方法生成的对称单元可能不是最优的。未来可以从其他网格化方法入手，考虑最优对称单元的构造。

［1］ BOSSAVIT A.Boundary value problems with symmetry and their approximation by finite elements［J］.SIAM Journal on Applied Mathematics，1993，53（5）：1352－1380.

［2］ SURESH K，SIRPOTDAR A.Automated symmetry exploitation in engineering analysis［J］.Engineering with Computers，2006，21（4）：304－311.

［3］ GUAN Zhenqun，SONG Chao，GU Yuanxian，et al.Recent advances of research on finite element mesh generation methods［J］.Journal of Computer Aided Design ＆ Computer Graphics，2003，15（1）：1－14（in Chinese）.［关振群，宋 超，顾元宪，等.有限元网格生成方法研究的新进展［J］.计算机辅助设计与图形学学报，2003，15（1）：1－14.］

［4］ RUPPERT J.A Delaunay refinement algorithm for quality 2－dimensional mesh generation ［J］.Journal of Algorithms，1995，18（3）：548－585.

［5］ UNGOR A.Off－centers：a new type of Steiner points for computing size－optimal quality－guaranteed Delaunay triangulations［J］.Computational Geometry：Theory and Applications，2009，42（2）：109－118.

［6］ ZENG W，SHI R，GU 段 .Global surface remeshing using symmetric delaunay triangulation in uniformization spaces［C］／／Proceedings of the 2011 8th International Symposium on Voronoi Diagrams in Science and Engineering.Washington，D.C.，USA：IEEE Computer Society，2011：160－169.

［7］ ANTHONY 段 ，FLATAU F A.Implementing ruppert's algorithm for generic curves in 2D ［EB／OL］.［2012－03－05］.http：／／www.imr.sandia.gov／papers／imr19／RNAnthony.pdf.

［8］ SHEWCHUK 段 .Triangle：engineering a 2Dquality mesh generator and delaunay triangulator［M］／／Applied Computational Geometry：Towards Geometric Engineering.Berlin，Germany：Springer－Verlag，1996：203－222.