基于几何公差描述逻辑的公差类型的自动生成

覃裕初，钟艳如，常 亮，黄美发

（1.桂林电子科技大学广西可信软件重点实验室，广西 桂林 541004；2.桂林电子科技大学机电工程学院，广西 桂林 541004）

0 引言

当前，主流的计算机辅助设计（Computer Aided Design，CAD）软件都具有强大的实体造型功能，但在对公差信息的处理上仍然有所滞后。在CETOL 6SigmaTM，eM－TolMateTM，VSA－GDTTM，VSA.3DTM和3DCSTM中，公差类型和公差值需要设计者手工指定。在CATIA.3DFDTTM中，大部分零件的可选公差类型可自动生成，但仍有部分非TTRS零件的可选公差类型无法自动生成。因此，如何自动地生成零件公差类型的问题，仍然没有得到完全解决［1］。

要解决好公差类型的自动生成问题，最重要的是要让计算机更好地理解它所表示的公差信息。针对公差信息尤其是几何公差信息在计算机中的表示问题，大量文献给出了各自的解决方法［1］。归结起来，可分为如下四大类：①基于面图的方法，如面向虚拟装配的方法［2－3］；②基于变动几何的方法，如基于特征技术与拓扑相连表面（Feature based Technologically and Topologically Related Surfaces，FTTRS）方法［4］和变动几何约束网络（Variational Geometric Constraint Network，VGCN）方法［5］；③基于公差带和基准参考框架的方法，如基于特征自由度的方法［6］和基于几何信息与加工特征的方法［7］；④基于数学定义的方法，如三维语义表示方法［8］和雅可比旋量表示方法［9］。一个完备的公差表示体系应满足三个要求：①能够在语义层面上准确地表示所有类型的几何公差；②能够准确地表示各种公差之间的关系；③应当符合标准且便于实际应用。在现有的各种表示方法中，还没有一种方法能满足所有要求且广泛应用于公差设计中［1］。因此，如何能让计算机更好地理解它所表示的公差信息，以便自动生成公差类型的问题，仍然需要继续研究。

描述逻辑（Description Logic，DL）是一类用于知识表示的形式化工具，它在软件工程、医疗信息系统、数字图书馆、自然语言处理等领域得到了成功应用［10］。在语义Web中，DL更是起到了举足轻重的作用，成为了W3C推荐的Web本体语言的逻辑基础［11］。DL具有较强的描述能力，同时又能保证相关推理的可判定性，且有高效的推理算法作为支撑［12］。DL的一个典型特征是可以在开世界假设的情况下进行推理。开世界假设是指如果从知识库中不能推导出某个公式，则认为不知道该公式是否成立。与之对应的是闭世界假设，即如果从知识库中不能推导出某个公式，则认为该公式不成立。由于CAD系统的开放性和分布性，往往需要采用开世界假设，在信息不完全的情况下进行推理。可见，DL能够有效地解决信息的被理解问题。

正因为DL有此优点，故将其引入到对公差类型自动生成的研究中。基于目前最新的几何公差标准（GB／T1182－2008）及空间关系与公差类型之间的映射关系［13］提出适合刻画几何公差的DL，构建基于该DL的几何公差表示模型，在此基础上研究计算机辅助公差类型的自动生成。

1 几何公差描述逻辑

在基于要素的CAD系统中，公差实质上是要素的几何变动，而要素的几何变动会产生某些特定的空间关系，故适合刻画公差信息的几何公差描述逻辑属于一种空间描述逻辑。空间描述逻辑主要由具体域、形式体系及Tableau判定算法三大部分组成［14］。要构建出几何公差描述逻辑，需要分别为其定义这三部分。

1.1 几何要素空间域

定义1 几何要素空间域Df是一个二元组（Δf，Φf），其中Δf是由所有几何要素组成的集合，Φf中包含如下表示两个几何要素之间空间关系的二元谓词：①约束关系谓词CON；②重合关系谓词COI；③分离关系谓词DIS；④包含关系谓词INC；⑤平行关系谓词PAR；⑥垂直关系谓词PER；⑦斜交关系谓词INT；⑧异面关系谓词NON；⑨配合关系谓词MAT。

在空间描述逻辑［14］中，描述逻辑所刻画的领域称为抽象域，实际应用的领域称为具体域。图1所示的是以圆柱为例，抽象域与具体域之间的对应关系。在抽象域中，要素feature－1和要素feature－2具有角色关系；通过特征has－feature的映射，feature－1和feature－2分别被映射到具体域中圆柱的拟合导出要素adf和实际组成要素rif；在具体域中，adf和rif具有空间谓词关系。

1.2 形式体系

几何公差描述逻辑GTDL（Df）的基本符号包括：①由概念名组成的集合NC；②由角色名组成的集合NR；③由抽象域个体名组成的集合NAI；④由具体域个体名组成的集合NCI；⑤由个体变元名组成的集合NIV；⑥由特征名组成的集合NF；⑦由谓词名组成的集合Φf；⑧构造符 ，，，∃，∀和r∃P；⑨其他符号，包括包含于号、定义号≡、圆括号（）、冒号：、逗号，和点号.。

定义2 GTDL（Df）的角色由以下产生式生成：

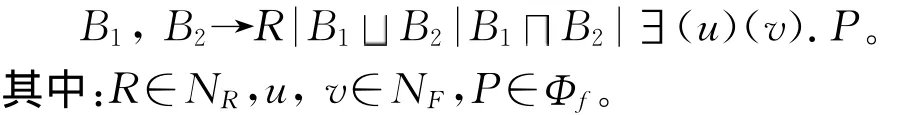
将形如R，B1B2，B1B2和∃（u）（v）.P的表达式分别称为原子角色、角色析取、角色合取和角色构成谓词限定。注意到原子角色和原子特征没有否定形式，角色之间不满足DeMorgan律。特别地，∃（u）（v）.P ＝∃（u）（v）. P。

定义3 GTDL（Df）的概念由以下产生式生成：

C，D →Ci｜ C｜CD｜∀R.C。其中Ci∈NC，R∈（NR∪NF）。

将形如Ci， C，CD和∀R.C的表达式分别称为原子概念、否定概念、概念析取和值限定。注意到概念之间满足DeMorgan律，因此可引入形如Top（顶概念）、Bot（底概念）、CD （概念合取）和∃R.C（存在性限定）的表达式，分别作为CC，Top，（CD）和 （∀R.C）的缩写。

若RN是一个角色名，R是一个角色，CN是一个概念名，C是一个概念，则形如RN≡R，CN≡C或CNC的表达式是术语公式，且前者称为角色定义式，后两者都称为概念定义式。术语公式的有限集称为术语表或TBox（记为T），当且仅当每个概念名最多在T中某个概念定义式的左边出现一次。

定义4 设ΔI是由抽象域个体组成的非空集合，ΔD是由具体域个体组成的非空集合，且ΔI∩ΔD＝Ø，则GTDL（Df）的解释是一个二元组I＝（ΔI，·I），其中·I是解释函数，它实现以下操作：

（1）概念名C解释为ΔI的一个子集，CI∈ΔI。

（2）角色名R解释为ΔI×ΔI的一个子集，RI∈ΔI×ΔI。

（3）特征名f解释为一个从ΔI到ΔD∪ΔI的部分函数fI：ΔI→（ΔD∪ΔI）。

此外，解释函数·I还必须满足以下等式：

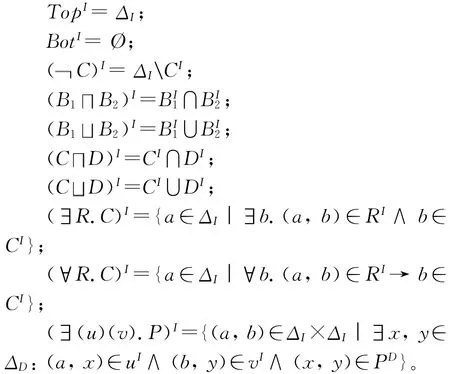
一个解释是：I是一个TBox T的模型，当且仅当对T中所有形如RN≡R的术语公式都有RNI＝RI，所有形如CN≡C的术语公式都有CNI＝CI，以及所有形如CNC的术语公式都有CNICI。

定义5 令NAI∩NCI＝Ø，若C是一个概念，R是一个角色，f是一个特征名，P∈Φf，a，b∈NAI，x∈NAI∪NCI，x1，x2∈NCI，则以下表达式都是断言公式：①a：C；②（a，b）：R；③（a，x）：f；④（x1，x2）：P。

断言公式的有限集称为ABox（记为A）。一个解释I是A的一个模型，当且仅当对A中所有形如a：C的断言公式都有aI∈CI，所有形如（a，b）：R的断言公式都有（aI，bI）∈RI，所有形如（a，x）：f的断言公式都有fI（aI）＝xI和所有形如（x1，x2）：P的断言公式都有（x1I，x2I）∈PD。

将由术语公式和断言公式组成的一个有限集合称为知识库，记为KB＝｛T，A｝。其中：T表示TBox，A表示ABox。一个解释I是KB的一个模型，当且仅当I同时是A和T的模型。

定义6 设ψ是一个断言公式，KB是一个知识库，称ψ相对于KB是一致的，当且仅当存在某个模型I使得KBψ；称ψ相对于KB是不一致的，当且仅当没有一个模型I使得KBψ。

1.3 Tableau判定算法

GTDL（Df）断言公式的一致性判定问题是一个基于ABox A在特定规则下的扩展问题，规则将A转化为与其一致性等价的“简单的”ABox Ai，直到所有的Ai均包含冲突（断言公式是不一致的），或者有某个Ai是完全的（断言公式是一致的）。因此，在给出判定算法之前，需先研究扩展规则及冲突和完全的定义。

定义7 设在某一个ABox A 中，R，B1和B2为角色，C和D为概念，a和b为个体，则扩展规则将ABox A扩展为其后继ABox A′，规则如下：

（5）（R∃C）：若a：∃R.C∈A，且b：C∉A，则A′→A∪｛（a，b）：R，b：C｝。

（6）（R∀C）：若a：∀R.C∈A，且b：C∉A，则A′→A∪｛b：C｝。

（7）（Rr∃P）：若（a，b）：∃（u）（v）.P∈A，且（x，y）：P∉A，则A′→A∪｛（a，x）：u，（b，y）：v，（x，y）：P｝。

定义8 设C∈NC，f∈NF，P∈Φf，a，b∈NAI，x，y∈NCI，则一个ABox A是不一致的，当且仅当它包含以下任一冲突：

（1）抽象域冲突，a：C∈A且a： C∈A。

（2）特征域冲突，（a，x）：f ∈A且（a，b）：f∈A。

（3）具体域冲突，（x，y）：P∈A且（x，y）：P∈A。

（4）所有域冲突，（a，x）：f∈A且a ：∀f.C∈A。

否则，ABox A就是一致的。

定义9 一个ABox A是完全的，当且仅当A是一致的且对A已无法再应用任何扩展规则。

有了以上扩展规则和定义，可得GTDL（Df）的Tableau判定算法，具体如下：

算法1 设A0为初始ABox，S为临时变量，ApplyRules（A）表示对A的应用扩展规则，complete，consistent和inconsistent分别表示完全的、一致的和不一致的，则Tableau判定算法的伪代码描述如下：

procedure GTDL（Df）－Tableau（A0）

S← ｛A0｝；

while ApplyRules（A）（A∈S）do S←（S﹨｛A｝）∪ApplyRules（A）

if there is an ABox Aithat is complete then return A0is consistent

else return A0is inconsistent end GTDL（Df）－Tableau

2 公差类型的自动生成

2.1 几何公差的GTDL（Df）表示模型

为了使产品几何规范与几何要素紧密相连，Srinivasan［15］根据对称群理论，将GPS中的理想要素分为如表1所示的7个恒定类。

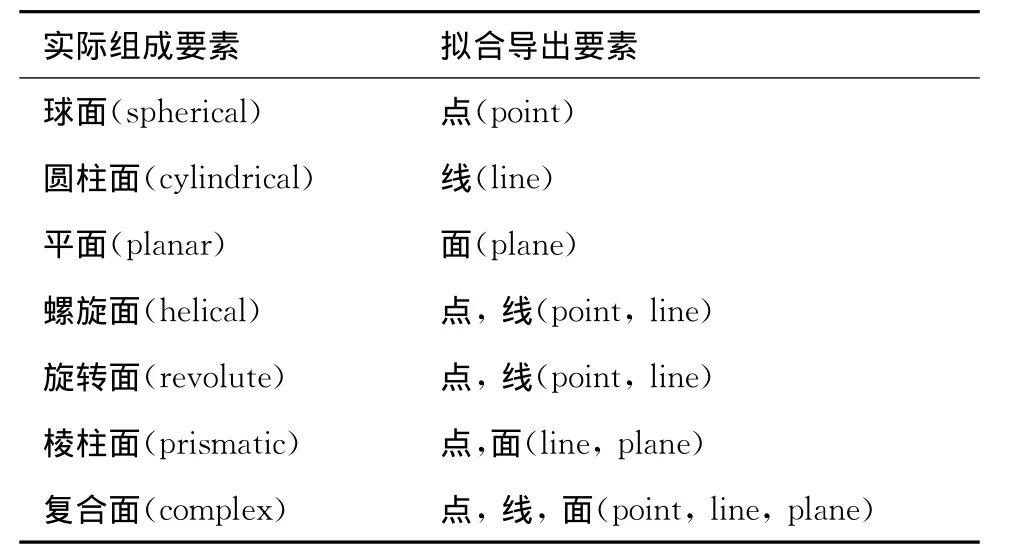
表1 GPS中的7个恒定类

基于7个恒定类，几何变动可划分为自参考几何变动和互参考几何变动两大类［5］。根据GB／T 1182－2008对几何公差的定义，且通过GTDL（Df）对空间关系的刻画，可得几何公差的GTDL（Df）表示模型，具体如表2所示。表中有关符号的含义分别如定义1、图1和表1所示。

表2 几何公差的GTDL（Df）表示模型

续表2

2.2 公差类型的自动生成算法

在现今商用的3D实体造型软件中，设计者可以方便地设计出复杂的装配体，设计出的装配体以配合特征树的形式存储在计算机中。Mathew等［16］设计的装配关系表生成（Liaison Table Generator，LTG）算法可从配合特征树中提取出各零件之间的装配约束关系。Mathew等［17］设计的装配配合提取（Assembly Mate Extraction，AME）算法可以从配合特征树中提取出零件的装配特征表面。基于几何公差的GTDL（Df）表示模型和GTDL（Df）的Tableau算法，可得公差类型的自动生成算法如下：

算法2 设“→”表示逻辑蕴含，对任意装配体，按以下步骤确定其中隐含的公差类型：

步骤1 构建产品的3D装配模型。根据产品的功能要求及各零件的理想尺寸，使用3D实体造型软件构建出产品的3D装配模型。

步骤2 解装配产品的3D装配模型。使用3D实体造型软件对产品的3D装配模型进行解装配。

步骤3 提取装配约束关系及装配特征表面。应用LTG算法提取出各零件之间的装配约束关系，应用AME算法提取出各零件的装配特征表面。

步骤4 构建表示零件之间的装配约束关系的ABox AP。根据提取到的装配约束关系，构建表示装配体中各零件之间装配约束关系的ABox AP。

步骤5 构建表示装配特征表面之间约束关系的ABox AA。根据构建的AP及提取到的各零件的装配特征表面，构建表示各零件的装配特征表面之间约束关系的ABox AA。

步骤6 构建表示几何要素之间空间关系的ABox AS。根据构建的AA和表1，构建表示装配特征表面的几何要素之间空间关系的ABox AS。

步骤7 确定可选公差类型。令x和y为几何要素空间域Df中的个体，TS为TBox且其组成元素为表2中的所有定义式，根据构建的AS，TS及GTDL（Df）的Tableau算法，执行GenerateTSEL（x，y）函数确定可选公差类型（记为集合TSEL）：

步骤8 确定最终标注的公差类型。根据产品的功能要求、公差标准、公差原则和设计经验，从TSEL中选出最终标注的公差类型（记为集合TFIN）。

功能要求需要根据实际情况分析，这里不作讨论。下面研究公差标准、公差原则及设计经验在确定TFIN时发挥的作用。公差原则包括独立原则和相关要求，相关要求又可分为包容要求、最大实体要求、最小实体要求和可逆要求。根据以上原则及设计经验，设计者在确定TFIN时应遵循以下规则［1］：

规则1 在GB／T标准中，包容要求仅适用于尺寸公差，而不适用于位置公差、方向公差及尺寸要素之间的内部关系。因此，在根据包容要求确定装配公差类型时应注意，几何公差主要用于控制几何要素的位置、方向及尺寸要素之间的内部关系。此外不适用于尺寸要素。

规则2 当要素的位置或形状独立于其尺寸时，不考虑形态尺寸。在考虑，及时，不需考虑形态尺寸、最大实体要求及最小实体要求。

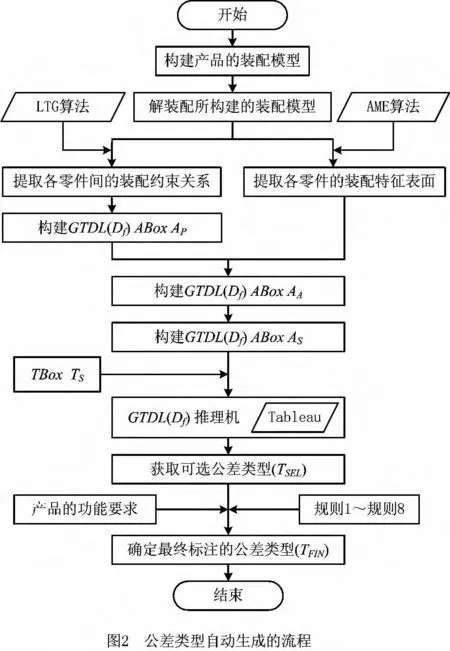
应用算法2，可实现计算机辅助公差类型的自动生成，其流程图如图2所示。

3 实例研究

以图3所示的齿轮减速器［1］为例，研究基于GTDL（Df）的公差类型的自动生成。为降低复杂度，本文仅研究减速器的两传动轴之间的传动结构。当装配减速器时，两个滚动轴承都可以看作标准零件，故将它们视为一个整体来研究，而不考虑它们内部各零件之间的公差类型。根据算法2，公差类型的自动生成步骤如下：

步骤1 构建产品的3D装配模型。根据减速器的功能要求及各零件的理想尺寸，使用Solid－Works可构建出减速器的3D装配模型，其局部视图如图3所示。

步骤2 解装配产品的3D装配模型。根据减速器的结构，使用SolidWorks对其3D装配模型进行解装配。减速器的传动结构的解装配图如图4所示。

步骤3 提取装配约束关系及装配特征表面。应用LTG算法提取各零件之间的装配约束关系，应用AME算法提取各零件的装配特征表面。

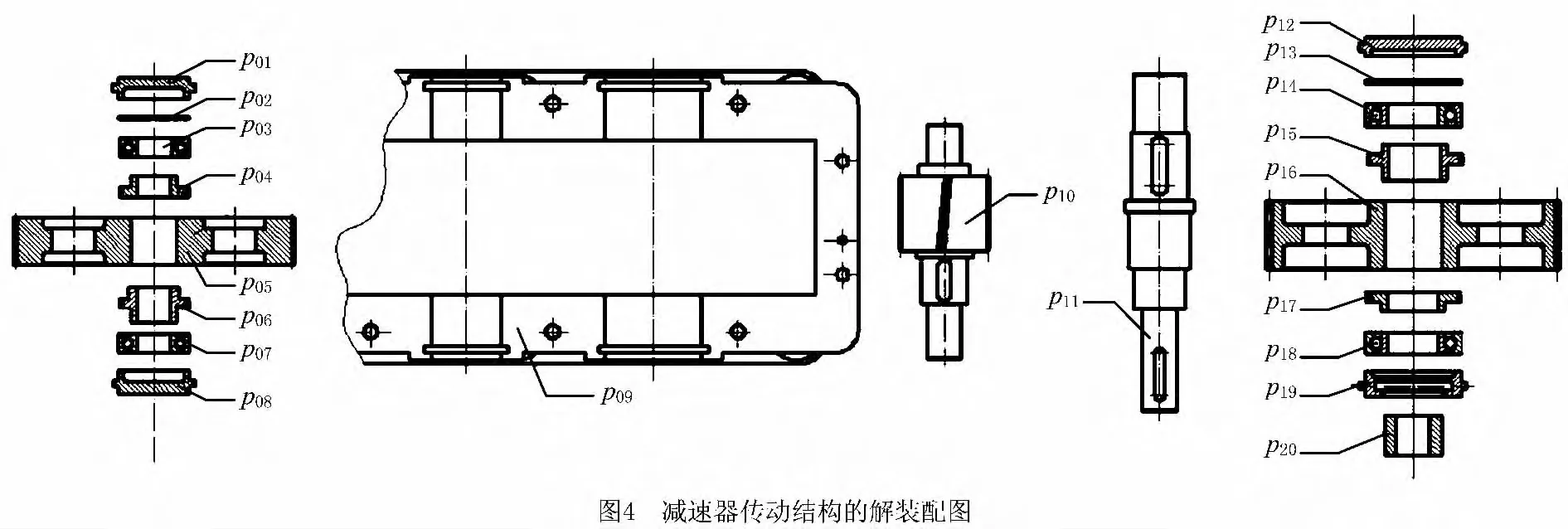
步骤4 构建表示零件之间装配约束关系的ABox AP。根据提取到的装配约束关系，构建表示减速器中各零件之间装配约束关系的ABox AP：

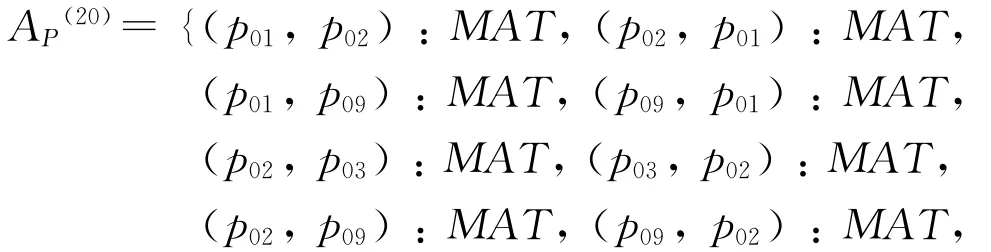
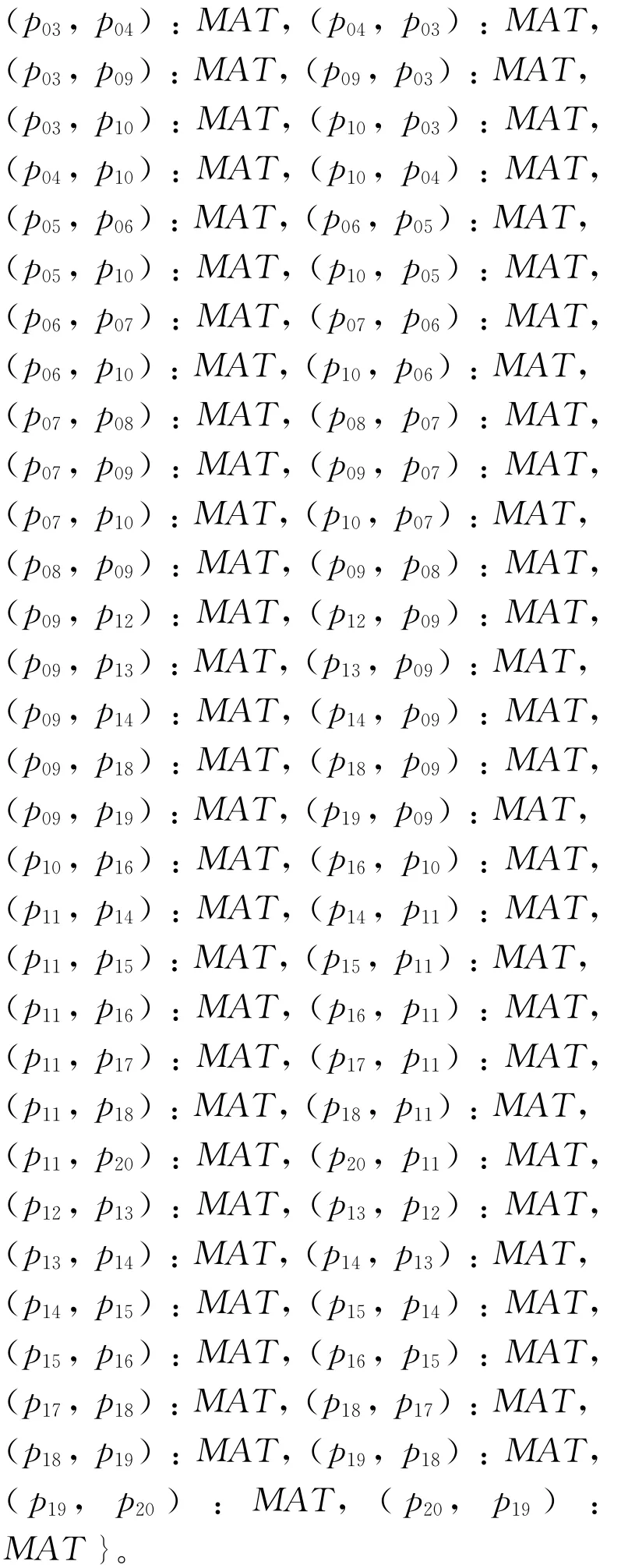
步骤5 构建表示装配特征表面之间约束关系的ABox AA。根据构建的AP（20）及提取到的各零件的装配特征表面，构建表示各零件的装配特征表面之间约束关系的ABox AA。下面以零件p10为例说明AA的构建过程。由AP（20）知，与p10有装配约束关系的零件有p03，p04，p05，p06，p07及p16。这7个零件的装配特征表面及其之间的装配约束关系如图5所示。根据图5可构建表示这7个零件的装配特征表面之间约束关系的ABox A（7）：

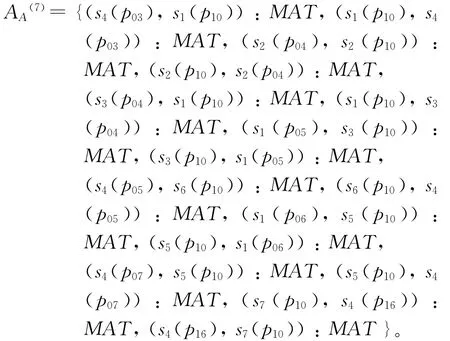
步骤6 构建表示几何要素之间空间关系的ABox AS。根据构建的AA（7）和表1，构建表示装配特征表面的几何要素之间空间关系的ABox AS（7）：（s4（p03），s1（p10））：MAT⇒（line，cylindrical），（line，line）⇒（line，cylindrical）：CON，（line，line）：COI；（s2（p04），s2（p10））：MAT⇒（plane，planar），（plane，plane）⇒ （plane，planar）：CON，（plane，plane）：COI；（s3（p04），s1（p10））：MAT⇒（line，cylindrical），（line，line）⇒（line，cylindrical）：CON，（line，line）：COI；（s1（p05），s3（p10））：MAT⇒（plane，planar），

步骤7 确定可选公差类型。根据AS（7），TS（如表2）及算法1，执行GenerateTSEL（x，y）函数确定 TSEL。例如，为了确定 TSEL（s4（p03），s1（p10）），需 要 执 行 GenerateTSEL（s4（p03），s1（p10）），此时问题转化为判定（TS∪AS（7））（s4（p03），s1（p10））：S（i）（i＝1，2，…，15）是否成立。下面以判定（TS∪AS（7））（s4（p03），s1（p10））：IsStraightness是否成立为例，跟踪GTDL（Df）推理机的推理过程。首先，将结论否定并加入AS（7），且化为否定范式后得ABox A1：

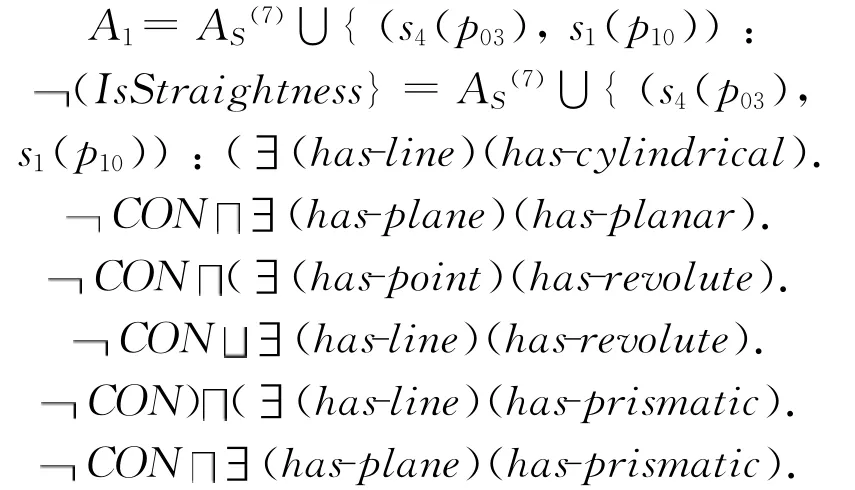
4 讨论

本文提出了基于GTDL（Df）的公差类型的自动生成方法，该方法以3D实体造型软件绘制的装配体为输入，经过解装配、提取相关信息、构建相应的ABox、确定可选公差类型及选定标注公差类型等步骤，确定装配体中应当标注的公差类型。与其他方法相比，本文方法有以下优点：①输入比较简单且输出符合实际要求。应用该方法时只需输入由3D实体造型软件所绘制的装配体，经过解装配、提取相关信息、构建相应的ABox及GTDL（Df）推理等步骤，本文方法会输出供设计者选择的多个公差类型，在这些公差类型中，总有部分公差类型符合实际要求。②可较好地应用于复杂的装配体。无论装配体是简单还是复杂，只要绘制出其3D装配模型，其余的步骤（最后一步除外）便可由计算机自动完成。③可在开世界假设的情况下推理。由于使用描述逻辑作为公差信息表示与推理的工具，本文方法具备了一定的智能性，它可以在信息不完全的情况下推理。④能够在语义层面上表示公差信息，且符合标准及便于实际应用。

然而，本文方法亦存在如下不足：①可自动生成可选公差类型，最终标注哪几种公差类型需要设计者手工选定。这个问题是当前大多数公差类型生成方法的瓶颈，已经商用的CATIA.3DFDTTM软件也存在该问题。②无法区分各种可选公差类型之间的细微差别，这也正是该方法仅能自动生成可选公差类型而非最终标注公差类型的根本原因。③只适用于刚性零件，不适用于非刚性零件，这个问题也是CATIA.3DFDTTM软件存在的问题。

5 结束语

本文提出了几何公差描述逻辑GTDL（Df），给出了GTDL（Df）的Tableau判定算法，构建了几何公差的GTDL（Df）表示模型，设计了公差类型的自动生成算法，并通过工程实例验证了生成算法的有效性。进一步研究可从以下方面着手：研究如何进一步减少生成的可选公差类型的数目；研究非刚性零件公差类型的生成；研究可选公差值的生成与公差的优化设计；开发GTDL（Df）推理机，构建基于GTDL（Df）的公差类型生成知识库系统，在此基础上开发计算机辅助公差类型生成软件。

［1］ ZHANG Yi，LI Zongbin，GAO Jianmin，et al.New reasoning algorithm for assembly tolerance specifications and corresponding tolerance zone types［J］.Computer－Aided Design，2011，43（12）：1606－1628.

［2］ WANG Heng，NING Ruxin.Product toleranced model oriented to virtual assembly［J］.Computer Integrated Manufacturing Systems，2006，12（7）：961－975（in Chinese）.［王 恒，宁汝新.面向虚拟装配的产品公差模型［J］.计算机集成制造系统，2006，12（7）：961－975.］

［3］ XIONG Zhenqi，LIU Jianhua，NING Ruxin，et al.Hybrid tolerance modeling for virtual product assembly［J］.Journal of Computer－Aided Design ＆ Computer Graphics，2008，20（12）：1609－1616（in Chinese）.［熊珍琦.刘检华，宁汝新，等.面向虚拟装配的产品公差混合建模技术［J］.计算机辅助设计与图形学学报，2008，20（12）：1609－1616.］

［4］ LIU Yusheng，GAO Shuming，WU Zhaotong，et al.Hierarchical representation model and its realization of tolerance based on feature［J］.Journal of Mechanical Engineering，2003，39（3）：1－7（in Chinese）.［刘玉生，高曙明，吴昭同，等.基于特征的层次式公差信息表示模型及其实现［J］.机械工程学报，2003，39（3）：1－7.］

［5］ HU Jie，XIONG Guangleng，WU Zhaotong.A variational geometric constraints network for a tolerance types specification［J］.The International Journal of Advanced Manufacturing Technology，2004，24（3／4）：214－222.

［6］ HUANG Meifa，ZHONG Yanru.A new model for concurrent tolerancing in CAD system［J］.China Mechanical Engineering，2004，15（18）：1623－1626（in Chinese）.［黄美发，钟艳如.CAD系统中并行公差的建模方法［J］.中国机械工程，2004，15（18）：1623－1626.］

［7］ TANG Censhu，CHU Xuening，SUN Xiwu，et al.Machining feature recognition based on geometry and tolerance information［J］.Computer Integrated Manufacturing Systems，2010，16（2）：256－262（in Chinese）.［汤岑书，褚学宁，孙习武，等.基于几何与公差信息的加工特征识别方法［J］.计算机集成制造系统，2010，16（2）：256－262.］

［8］ LIU Yusheng，GAO Shuming，WU Zhaotong，et al.A representation method of 3Dtolerance semantics based on mathematical definition［J］.China Mechanical Engineering，2003，14（3）：241－245（in Chinese）.［刘玉生，高曙明，吴昭同，等.一种基于数学定义的三维公差语义表示方法［J］.中国机械工程，2003，14（3）：241－245.］

［9］ ZHANG Weimin，CHEN Can，LI Pengzhong，et al.Tolerance modeling in actual working condition based on Jacobian－Torsor theory［J］.Computer Integrated Manufacturing Systems，2011，17（1）：77－83（in Chinese）.［张为民，陈 灿，李鹏忠，等.基于雅可比旋量法的实际工况公差建模［J］.计算机集成制造系统，2011，17（1）：77－83.］

［10］ BAADER F，CALVANESE D，MCGUINNES 段 ，et al.The description logic handbook：theory，implementation and applications［M］.Cambridge，UK：Cambridge University Press，2007.

［11］ HORROCKS I，PATEL－SCHNEIDER 段 ，HARMELEN F V.From SHIQ and RDF to OWL：the making of a Web ontology language［J］.Journal of Web Semantics，2003，1（1）：7－26.

［12］ CHANG Liang，SHI Zhongzhi，QIU Lirong，et al.A tableau decision algorithm for dynamic description logic［J］.Chinese Journal of Computers，2008，31（6）：896－909（in Chinese）.［常 亮，史忠植，邱莉榕，等.动态描述逻辑的Tableau判定算法［J］.计算机学报，2008，31（6）：896－909.］

［13］ ZHONG Yanru，QIN Yuchu，HUANG Meifa et al.A Tolerance Representation Model Based on Feature Surfaces and Spatial Relations［J］.Journal of Mechanical Engineering，2013，49（11）：161－170.［钟艳如，覃裕初，黄美发等.基于特征表面和空间关系的公差表示模型［J］.机械工程学报，2013，49（11）：161－170.］

［14］ HAARSLEV V，LUTZ C，MOLLER R.A description logic with concrete domains and a role－forming predicate operator［J］.Journal of Logic and Computation，1999，9（3）：351－384.

［15］ SRINIVASAN V.A geometrical product specification language based on a classification of symmetry groups［J］.Computer－Aided Design，1999，31（11）：659－668.

［16］ MATHEW 段 ，RAO R O P.A novel method of using API to generate liaison relationships from an assembly［J］.Journal of Software Engineering ＆ Applications，2010，3（2）：167－175.

［17］ MATHEW 段 ，RAO R O P.A CAD system for extraction of mating features in an assembly［J］.Assembly Automation，2010，30（2）：142－146.