退化试验下数控系统可靠性快速贝叶斯评定方法研究

李 彬，刘学江

（天津职业技术师范大学机械工程学院，天津 300222）

0 引言

目前，国产数控系统市场占有率低的重要原因之一是其可靠度相对偏低［1-3］。数控系统可靠性评估是一项耗财、耗时的工作。要实现数控系统可靠性快速评估，可从以下几方面展开：一是研究快速获取样本失效数据的试验方法；二是研究由较少的样本失效数据完成可靠性评估的方法；三是研究如何充分利用试验过程中包含的可靠性信息。

在可靠性评估工作中对试验信息的利用，可只利用一维信息，即时间；也可利用二维信息，即时间、失效模式或退化量［4-7］。

数控系统可能存在多种失效模式，即数控系统失效是多种失效模式竞争的结果。已有相关学者建立了竞争失效场合ALT的竞争失效模型和极大似然估计（MLE）方法。但基于MLE的统计方法，需要较大的样本量才能获得优良的估计性质。Bunea［8］，张志华［9］等研 究 了 竞 争 失 效场合 ALT 的Bayes估计方法。潭源源采用Dirichlet分布作为先验分布，研究了指数分布下竞争失效场合恒定单应力ALT的非完整数据的Bayes分析方法［10］。

数控系统主要是由元器件、印刷电路板、电连接器、液晶屏和绝缘材料等组成的，而这些组件在工作过程中存在性能退化、性能退化存在加速性的现象已经得到了研究者的证实［11-13］。因此，将通过设计退化试验方案，研究数控系统的可靠性快速评估方法。

1 数控系统双应力步加退化试验

现场跟踪试验故障数据来源于生产一线，其优点是在理想情况下能真实反映数控系统实际的工作状态或使用情况，缺点是时间较长、故障记录与分析受制于操作者水平。需要说明的是：可靠性是指产品在规定的条件下和规定的时间内，完成规定功能的概率。试验方法的不同虽然会引起可靠性指标的细微差别，但可靠性评估的方法和原理是相同的。因此，有必要在失效机理不变的前提下，开展温-湿双应力步加退化试验，缩短试验周期，降低试验费用。温-湿双应力步加退化试验下，数控系统快速贝叶斯评估方案如图1所示。

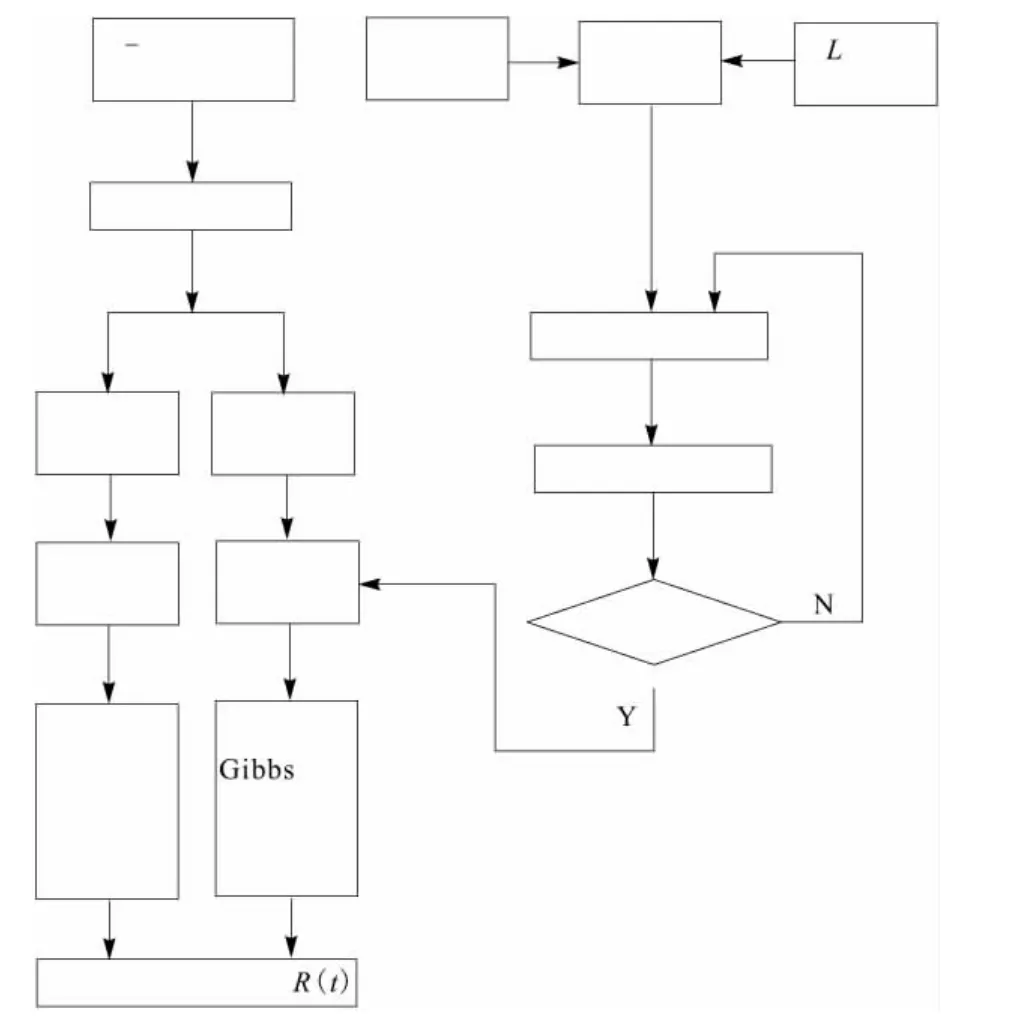
图1 数控系统快速贝叶斯评估方案

基于前期的FMECA分析可知，温度和湿度是影响数控系统可靠性的主要环境因素。因此，拟采用温-湿双应力对数控系统进行双应力步加退化试验。

对进行温-湿双应力步加退化试验的数控系统来讲，其故障往往是由于系统中某个部件或组件出现故障导致的，且这种故障通常是可修复的。数控系统发生故障后经过修复又重新投入工作，因此，可以用随机点过程来描述其故障数据。一般认为数控系统经过维修后，其可靠性又回到最初的水平，即故障间隔时间独立同分布，一般用齐次泊松过程描述；若认为数控系统经维修后，其可靠度等于故障前瞬间的可靠度，可用非齐次泊松过程描述。

对于可修复的数控系统，考虑到成本高，维修时并非完全维修，引入带位置参数的Weibull过程，强度函数可写为：

温-湿双应力步加试验下的加速方程采用Peck模型：

将随机过程与加速模型结合起来，则式（1）可变形为：

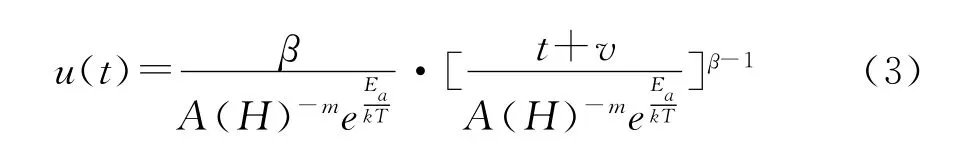
由于位置参数反映数控系统的初始状态，即使使用条件不同，其值也都是相等的。因此，位置参数不随应力条件的变化而变化。

对温-湿双应力联合作用下的完整数据、截尾数据混合的情况，采用多元混合数据回归分析方法。针对三参数Weibull分布情况，通过对数变换转化为极值分布，再进行多元混合数据回归分析的处理。

设y为服从极值分布的随机变量，其分布函数为：

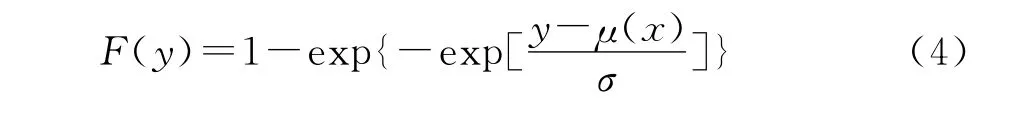
μ（x）为位置参数；σ为尺度参数。若μ（x）与x=（x1，x2，…，xr）T之间存在线性关系，则回归方程可表示为：

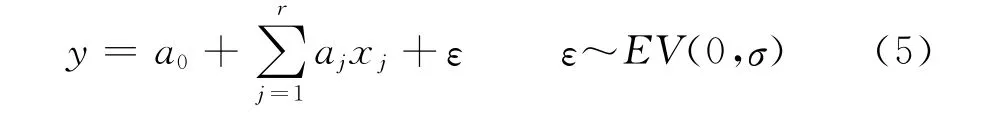
2 基于竞争失效模型的可靠性评估

针对数控系统失效模式并不单一的问题，建立竞争失效模型。针对竞争失效场合加速退化试验数据可能存在的完整数据、截尾数据和失效模式未确定数据这几种类型，Bayes分析的基本思路是：首先选择先验分布形式，确定先验分布表达式，对完整数据和截尾数据进行Bayes分析，得到后验分布表达式；然后以最近一次得到的后验分布作为先验分布，逐一对失效模式未确定数据点进行Bayes估计，得到后验分布及其表达式；最后，通过加速模型外推正常应力水平下的参数评估值。

针对联合后验分布很难采用数值积分得到后验统计的问题，采用Gibbs抽样方法计算后验统计，进而求出参数的估计值。其基本思想是从满条件分布中的迭代进行抽样，当迭代次数足够大时，就可得到来自联合后验分布的样本，进而也得到了来自边缘分布的样本。Gibbs抽样的关键在于如何从各个满条件分布抽样，当满条件分布不是标准分布函数时，对其抽样存在一定的困难，可采用标准取舍抽样得到满条件分布抽样值。

在温-湿双应力步加退化试验过程中，既存在突发性失效，也存在退化失效。对突发性失效采用上面提到的加速试验数据分析方法即可。对于退化失效，基于随机过程和温-湿双应力加速模型建立加速退化模型，确定失效阈值，则数控系统的失效时间为性能退化量首次到达失效阈值的时间T，即将退化量分布模型转化为T的分布，再与突发性失效数据组合建立竞争失效模型。

3 建立加速退化模型

B-S分布是概率物理分析中一个重要的疲劳失效模型，目前对该模型的加速应力分析主要基于寿命数据，此处用加速退化数据进行数控系统可靠性统计推断。数控系统在周期负载作用下特征量逐渐退化，一个负载周期可认为是一个时间单位，第i个负载周期内引起的特征量退化微小增量di是一个随机变量，其分布受负载影响。假设该随机变量值均为μd，方差为，则经n个负载周期后，数控系统的积累退化量xn=di。根据中心极限定理，当n很大时，有随机变量（di-nμd／）的分布收敛于标准正态分布，则到t时刻，退化量x（t）的均值函数为：

当退化失效阈值为l时，数控系统t时刻的失效概率为：

由以上分析可知，高应力水平在单位时间内引起的退化增量要大，即受应力影响，当加速应力为温 -湿双应力时，有μd=a（H）-me，B-S分布的加速退化方程为：

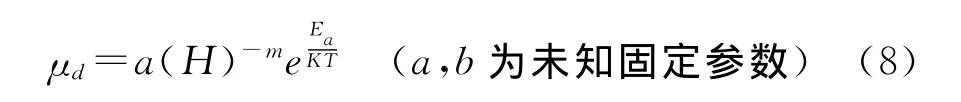
在温-湿双应力步加试验下，数控系统既存在突发失效也存在退化失效，则需考虑突发失效与退化过程相关时的竞争失效问题。不失一般性，设数控系统性能随着时间的增加而逐渐退化，性能退化量记为x（t），它是时间连续的随机变量，退化失效阈值为l，即当x（t）≥l时产品发生退化失效；另外，数控系统还具有多个突发失效模式，突发失效可能受产品退化量的影响，一般情况下，某一时刻退化量越大，突发失效出现的可能性也越大。

显然，t时刻退化量x的大小是一个随机变量，设其分布函数为G（x，t），相应的密度函数为g（x，t）。数控系统发生退化失效的时间记为Td，根据退化型失效的失效判据，仅考虑退化时其在t时刻的失效概率为：

｛G（x，t）；t＞0｝是一个带有时变参数的分布族，设其未知时变参数的分布族为：

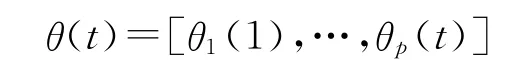
设突发失效时间为Tt，突发失效在某一时刻出现的概率受退化量x的影响，因此，突发失效时间Tt的危险函数可表示为λt（t｜x）。

则其条件生存函数及条件失效分布函数分别为：

数控系统失效为突发失效与退化失效的结果，根据以上各式，t时刻其可靠度为：

4 结束语

经过Jeffreys，Robbins，Savage等学者的努力，Bayes方法在理论和方法上得到不断完善。在国外，Bayes学派已发展为一个非常有影响的统计学派。Bayes方法在美国国防科技领域以及Bayes方法在我国武器系统的成功应用，说明在可靠性研究中应用Bayes方法具有成功的范例，并且也适宜向数控系统可靠性快速评估领域进行推广。

［1］遇立基.关于数控系统产业化发展和市场培育的建议［J］.世界制造与装备市场，2006，（4）：37-39.

［2］李本忍，李家霁.对我国数控系统可靠性的一些看法［J］.中国机械工程，1998，9（5）：11-13.

［3］贾亚洲.数控系统可靠性国内外现状及对策［J］.中国制造业信息化，2006，（6）：51-53.

［4］Chen Z H，Zheng H R.Lifetime distribution based degradation analysis［J］.IEEE Transactions on Reliability，2005，54（1）：3-10.

［5］峁诗松，汤银才，王玲玲.加速寿命试验［M］.北京：高等教育出版社，2008.

［6］姚增起.系统退化和系统可靠性研究［D］.北京：中国科学院自动化研究所，1988.

［7］潘 骏，刘红杰，陈文华，等.基于步进加速退化试验的航天电连接器接触可靠性评估［J］.中国机械工程，2011，22（10）：1197-1120.

［8］Bunea C，Mazzuchi T A.Bayesian accelerated life testing under competing failure modes［C］.Proceeding of Annual Reliability and Maintainability Symposium，2005.152-157.

［9］张志华，峁诗松.指数分布场合下竞争失效产品加速寿命试验的Bayes估计［J］.应用概率统计，1998，14（1）：2073-2100.

［10］潭源源，张春华，陈 循.基于Dirichlet先验分布的的加速寿命实验的Bayes分析［J］.宇航学报，2010，31（6）：1678-1684.

［11］吴 军，邵新宇，邓 超，等.基于性能劣化的可靠性预测与系统开发［J］.计算机集成制造系统，2011，17（1）：191-197.

［12］邹心遥，姚若河.小样本统计理论及IC可靠性评估［J］.控制与决策，2008，23（3）：241-245，250.

［13］贾占强，蔡金燕，梁玉英，等.基于综合环境加速寿命试验的电子装备故障预测研究［J］.电子学报，2009，36（6）：1277-1282.