城市典型生命线系统耦联多维测度方法研究
2013-08-26索玮岚
索玮岚 陈 锐
(中国科学院科技政策与管理科学研究所,北京100190)
城市生命线是维系城市功能的基础性工程,包括交通、供水、供热、电力、燃气、通讯等系统[1-2],其具有公共性高[3-4]、耦联性强[5-6]、脆弱性显著[7-8]等特点。在城市生命线诸多系统中,以供热、电力、燃气(简称热电气)系统为代表的城市典型生命线又构成了城市运行的必要条件[9-10]。虽然城市典型生命线各系统独立运营,但其在空间布施、功能交互等方面具有的系统耦联性使得某一系统的异常往往会诱发其他系统的不良连锁效应,导致公众的生命和财产损失[5,7]。城市典型生命线系统耦联测度不同于一般的测度问题,其具有很强的复杂性。一方面,城市典型生命线在设施布局、运行功能等多个维度存在系统耦联性[11-14],且这种耦联性通常具有传导效应[15-16];另一方面,城市典型生命线各维度耦联机理的不同导致其耦联性具有方向和强弱的差异,而且各维度耦联信息获取的手段和表现形式也各有不同[13-14]。因此,如何采用有效的测度方法解决城市典型生命线系统耦联测度问题是一个重要的课题,不仅有助于相关部门识别各系统之间的复杂耦联关系、还可以为优化城市典型生命线的布局与运行提供指导和支持。
目前,国内外关于城市生命线系统耦联测度方法的研究尚处于探索阶段。其中,Ouyang等[17]定义了耦联系数来量化城市生命线的系统耦联性,并借助仿真方法模拟出系统耦联度;张明媛等[18]使用0-1信息来量化城市生命线的系统耦联性,并采用基于脆性理论的方法计算了系统耦联度;Ge等[19]使用0-1信息来量化城市生命线的空间地理耦联性,并研发了基于GIS和Petri网技术的仿真器用以模拟系统耦联度;Johansson和Hassel[20]使用城市生命线节点之间连接线路的数量来刻画系统耦联性,并采用基于网络理论的建模方法计算了系统耦联度;Zhang和Peeta[21]采用0-9分来量化城市生命线的系统耦联性,并采用基于可计算一般均衡理论的建模方法计算了系统耦联度。然而,上述测度方法在应用过程中存在如下不足之处:①大多采用0-1信息来描述系统耦联性的有无,信息粒度会比较粗糙,还需要针对系统耦联性的方向及强弱给出更为全面、精确的描述;②没有考虑城市典型生命线系统耦联诱发的传导效应,可能会影响测度结果的准确性;③没有考虑耦联机理差异会造成耦联信息形式的不同,对各种形式耦联信息的处理和集结问题尚未涉及。因此,需要研究新的测度方法来解决城市典型生命线系统耦联测度问题。
鉴于此,本文首先从结构性、功能性和阶段性维度入手进行城市典型生命线系统耦联机理分析;然后,提出一种基于主客观信息的城市典型生命线系统耦联多维测度方法。该方法利用二元语义表示模型将语言短语形式的功能性和阶段性维度耦联信息转化为二元语义形式,并通过对决策试验和评价实验室(DEMATEL)法进行扩展,实现对数值形式的结构性维度耦联信息与二元语义形式的功能性和阶段性维度耦联信息的处理和集结,进而确定各系统的中心耦联度和关系耦联度,便于相关部门明晰各系统耦联的强弱及类型。本文提出的测度方法克服了现有测度方法的局限性,不仅同时考虑了耦联信息的方向和强弱以及耦联传导效应,还充分考虑了耦联信息形式的差异,并在信息处理和集结过程中有效地避免了信息损失。
1 城市典型生命线系统耦联机理分析
城市典型生命线系统耦联情境可用G={A(G),R(G)}表示,其中,A(G)={Ai|i=1,2,...n;n≥2}为城市典型生命线系统集合,R(G)={(Ai,Aj)|Ai,Aj∈A(G),i≠j,i,j=1,2,...,n}为城市典型生命线系统耦联关系集合。各系统之间耦联关系的衍生原因各异,而且耦联的方向和强弱也各有不同。在城市典型生命线系统耦联示意图(见图1)中,“●”、“▲”和“■”分别表示城市典型生命线系统A1、A2和A3的节点,对应供热系统的热力站、电力系统的变电站或燃气系统的门站等,“-”表示各系统节点控制的管线,“→”和“ ”分别表示不同系统节点之间的直接和间接耦联关系,箭头指明耦联方向,线的粗细反映耦联强弱。基于已有文献[11-14]的研究成果,本文将从各系统之间耦联关系衍生的原因入手,分别从结构性、功能性和阶段性三个维度进行城市典型生命线系统耦联机理分析。
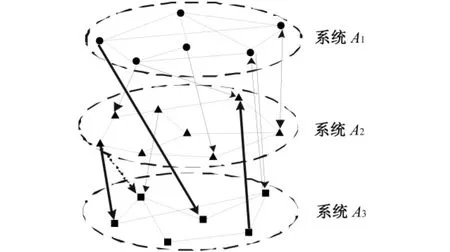
图1 城市典型生命线系统耦联示意图Fig.1 Illustration of system coupling of urban typical lifelines
1.1 结构性耦联
结构性耦联指由于城市典型生命线各系统相关设施(如节点、管线等)在空间上毗邻或交织而产生的互相影响关系。例如,在地下管线密集的城市中心区,供热与燃气管线一起铺设在通行的综合地沟内,任一系统管线的破坏都会干扰相邻系统的正常运行。记R1(G)={(Ai,Aj)|Ai,Aj∈A(G),i≠j,i,j=1,2,...,n}为城市典型生命线系统结构性耦联关系集合,可通过GIS技术采集、统计和汇总城市典型生命线设施布局的客观地理参照特征来获取耦联信息,其通常表现为数值形式,且有R1(G)⊂R(G)。各系统之间的结构性耦联为双向对等关系,故有R1(Ai,Aj)=R1(Aj,Ai),i≠j,i,j=1,2,...n。这里不考虑系统自身的结构性耦联,即 R1(Ai,Ai)∈φ,i=1,2,...,n。
1.2 功能性耦联
功能性耦联指常态下由于城市典型生命线之间的功能交互(如一个系统的输出为其他系统的输入)或依赖(如某个系统的运行需要其他系统提供必要的能源支撑)而产生的互相影响关系。例如,燃气系统输出的天然气是供热系统的主要原料,其稳定供给在一定程度上也保障了供热系统的正常运行;供热系统相关设备的运转离不开电力系统的支撑,安全可靠的供电有利于供热系统的稳定运行。记 R2(G)={(Ai,Aj)|Ai,Aj∈A(G),i≠j,i,j=1,2,...,n}为城市典型生命线系统功能性耦联关系集合,可通过专家的主观判断来获取耦联信息,通常表现为语言短语形式,且有R2(G)⊂R(G)。各系统之间功能性耦联的方向和强弱各有不同,故有 R2(Ai,Aj)≠R2(Aj,Ai),i≠j,i,j=1,2,...,n。这里不考虑系统自身的功能性耦联,即 R2(Ai,Ai)∈φ,i=1,2,...,n。
1.3 阶段性耦联
阶段性耦联指由于突发破坏性事件(如地震、洪涝等自然灾害或施工违章、检修不当等人为事故)导致城市典型生命线在某个特定时期内持续的互相影响关系。例如,在北方采暖季,由于施工违章造成的供热管道破坏会影响周边居民的生活取暖,在维修期间居民会较多使用电暖设备,导致用电量的大幅增加从而给电力系统带来运行压力。记 R3(G)={(Ai,Aj)|Ai,Aj∈A(G),i≠j,i,j=1,2,...,n}为城市典型生命线系统阶段性耦联关系集合,可通过专家的主观判断来获取耦联信息,通常表现为语言短语形式,且有R3(G)⊂R(G)。各系统之间阶段性耦联的方向和强弱各异,故有 R3(Ai,Aj)≠R3(Aj,Ai),i≠j,i,j=1,2,...,n。这里不考虑系统自身的阶段性耦联,即 R3(Ai,Ai)∈φ,i=1,2,...,n。
综上,城市典型生命线在结构性、功能性和阶段性各维度的系统耦联性由设施空间毗邻、功能交互或依赖、突发破坏性事件等原因直接导致。然而现实中,由于城市典型生命线各系统管线的网络化布局,往往会诱发上述耦联性的传导效应[15-16],即衍生出系统之间的间接耦联。同时,耦联机理的差异使得耦联信息形式各有不同,如结构性耦联信息表现为数值形式,而功能性和阶段性耦联信息则表现为语言短语形式。在进行城市典型生命线系统耦联测度时,需要综合考虑系统之间的直接耦联和间接耦联以及耦联信息形式的差异。
2 基于主客观信息的城市典型生命线系统耦联多维测度方法
结合上述城市典型生命线系统耦联机理分析,给出一种基于主客观信息的系统耦联多维测度方法。首先,给出系统耦联测度问题描述;然后,给出系统耦联多维测度方法的原理与步骤。
2.1 问题描述
为便于分析,采用下列符号描述城市典型生命线系统耦联测度问题所涉及的集合和量。
A={A1,A2,...,An}:城市典型生命线系统集合(n≥2),其中,Ai为第 i个系统,i∈{1,2,...,n};
E={E1,E2,...,Em}:专家集合(m≥2),其中,Ek为第 k个专家,k∈{1,2,...,m};
S={S0,S1,...,Sg}:语言短语评价集合,其中,Su为第 u 个语言短语,u∈{0,1,...g};
Y=[yij]n×n:结构性耦联矩阵,其中,yij为通过 GIS 技术获取的反映系统Ai和Aj之间设施空间毗邻个数的耦联信息,i,j=1,2,...,n;
Zk=[zkij]n×n:功能性耦联矩阵,其中,zkij为专家 Ek针对常态下系统Ai对Aj的功能交互或依赖程度给出的耦联信息,zkij∈S,k=1,2,...,m,i,j=1,2,...,n;
Bk=[bkij]n×n:阶段性耦联矩阵,其中,bkij为专家 Ek针对突发破坏性事件衍生的系统Ai对Aj影响程度给出的耦联信息,bkij∈S,k=1,2,...,m,i,j=1,2,...,n;

本文要解决的问题是根据已知的结构性耦联矩阵Y=[yij]n×n,功能性耦联矩阵 Zk=[zkij]n×n,阶段性耦联矩阵Bk=[bkij]n×n和耦联维度权重向量 W,如何通过某种测度方法确定各系统的耦联度,进而识别城市典型生命线各系统之间的复杂耦联关系。
2.2 测度方法的原理与步骤
为了解决上述问题,本文给出一种基于主客观信息的城市典型生命线系统耦联多维测度方法,其原理与步骤描述如下。



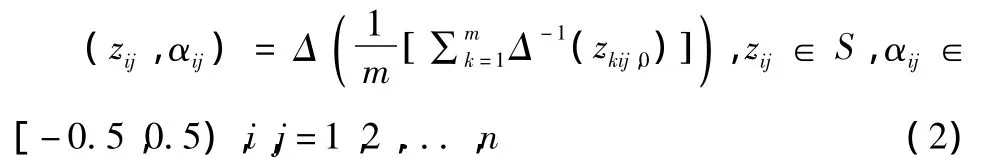




依据上述两个性质可得到系统间接耦联矩阵D=[dij]n×n,i,j=1,2,...,n,其计算公式为:

在此基础上,依据公式(9)可得到系统综合耦联矩阵T=[tij]n×n,其中,tij表示系统 Ai对 Aj的直接耦联与间接耦联程度的总和,即综合耦联程度,其计算公式为:

基于矩阵T确定各系统的中心耦联度hi和关系耦联度ri,其计算公式分别为
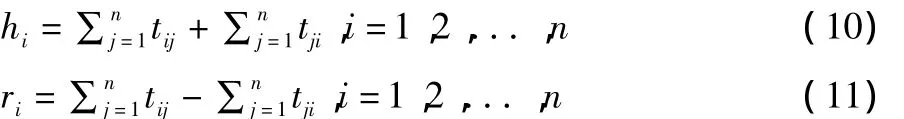
这里,中心耦联度hi表明系统Ai在城市典型生命线系统耦联中所起作用的大小,关系耦联度ri表明系统Ai的耦联类型。若ri>0,则表明Ai通过耦联性影响其他系统,为原因型耦联系统;若ri<0,则表明Ai受其他系统的耦联性影响,为结果型耦联系统。由此,相关部门可以根据hi和ri确定系统耦联的强弱和类型,并以此为依据采取针对性的策略优化城市典型生命线的布局与运行。
3 实例分析
某样区(简称C区)地处北京市南郊平原地带,近年来在城市规划与建设方面取得了迅猛发展。但随着聚居人口及工业生产规模的不断扩大,辖区内城市典型生命线的运行面临着诸多压力。为缓解当前压力并优化城市典型生命线的布局与运行,相关部门邀请了来自城市管理、系统工程等领域和热、电、气三大行业的15位专家,采用本文给出的方法对辖区内热、电、气(A1,A2,A3)之间的系统耦联进行测度。语言短语评价集合S={S0:No(没有耦联),S1:VL(非常弱的耦联),S2:L(弱耦联),S3:H(强耦联),S4:VH(非常强的耦联)}。耦联维度权重向量由组织者直接给出,W=(1/3,1/3,1/3)T。
首先,通过GIS技术采集、统计和汇总辖区内热电气设施布局的地理参照特征(如图2所示)。进而,根据图2可构建结构性耦联矩阵,即


图2 C区内热电气设施布局图Fig.2 Equipment placement of heating,electricity and gas systems in C area
其次,通过发放调查问卷获取15位专家给出的功能性和阶段性耦联信息(由于篇幅有限,这里不再罗列原始问卷信息),并依据公式(1)-(3)分别得到功能性和阶段性维度耦联群矩阵,即

然后,根据公式(4)-(6),分别得到结构性、功能性和阶段性各维度的耦联规范化矩阵,即

进一步地,根据公式(7)-(9),分别得到系统直接耦联矩阵、系统间接耦联矩阵和系统综合耦联矩阵,即

在此基础上,根据公式(10)-(11),分别计算出热电气各系统的中心耦联度和关系耦联度,结果如表1所示。从中可以看出,热电气各系统的中心耦联度排序为:A2≻A3≻A1,其中,供热系统A1为结果型耦联系统,电力、燃气系统A2和A3为原因型耦联系统。
依据表1中的系统耦联测度结果可知,电力系统A2在系统耦联中发挥了显著作用,因此在开展辖区内城市典型生命线布局与运行的优化工作时,应该重点加强电力系统的合理规划与网络改造。同时,相关部门可以结合系统耦联类型制定针对性的联调联动策略来提高辖区内城市典型生命线运行的全局优化效率,通过对原因型耦联系统的优化管理来良性促进结果型耦联系统的稳定运行。具体地,一方面,可以通过辖区内电网地缆化的实现来提高供电质量和可靠性,从而为供热系统各类设备的运转提供更加稳定的电力保障;另一方面,可以采用先进的管网优化设计模型在辖区内构建多气源、网络拓扑式燃气管网来保障燃气高效传输,进而为供热系统提供更充沛的能源供给。此外,还可以借助多平台、多传感器、多模态的遥感技术和计算机网络技术等构建热电气联调联动网络体系,实现对热电气系统运行态势的监测、分析、评估、模拟、预测与预警等,提高城市典型生命线应对风险的响应速度和效能。

表1 热电气各系统中心耦联度和关系耦联度的计算结果Tab.1 Computation results of prominence coupling degrees and relation coupling degrees of heating,electricity and gas systems
4 结论
系统耦联测度在城市典型生命线运行与管理过程中发挥着重要的作用。本文首先从机理分析入手,指出设施空间毗邻、功能交互或依赖、突发破坏性事件等原因造成城市典型生命线各系统在结构性、功能性和阶段性维度存在耦联性,且这种耦联性具有传导效应,并进一步指出各维度耦联机理的差异导致其耦联方向和强弱以及耦联信息形式各有不同;然后提出一种基于主客观信息的城市典型生命线系统耦联多维测度方法。本文提出的方法不仅同时考虑了系统耦联的方向和强弱以及耦联传导效应,还充分考虑了耦联信息形式的差异,并具有简单易操作、实用性强、无信息损失等特点,能够为相关部门识别城市典型生命线各系统之间的复杂耦联关系以及优化城市典型生命线的布局与运行提供有效的决策分析支持。此外,由于系统耦联性引发的传导效应往往导致城市典型生命线运行的风险性剧增,因此研究考虑系统耦联性的城市典型生命线综合风险评估方法将是进一步需要开展的工作。
(编辑:张 英)
References)
[1]Beavers J E.Advancing Mitigation Technologies and Disaster Response for Lifeline Systems[M].Reston,Virginia:ASCE Publications,2003.
[2]李宏男,柳春光.生命线工程系统减灾研究趋势与展望[J].大连理工大学学报,2005,45(6):931-936.[Li Hongnan,Liu Chunguang.Trends and Prospects for Research on Disaster Mitigation in Lifeline Engineering System[J].Journal of DaLian University of Technology,2005,45(6):931 -936.]
[3]尤建新,陈桂香,陈强.城市生命线系统的非工程防灾减灾[J].自然灾害学报,2006,15(5):194-198.[You Jianxin,Chen Guixiang, Chen Qiang. Non-structural Disaster Prevention and Reduction Measures of Urban Lifeline Systems[J].Journal of Natural Disasters,2006,15(5):194 -198.]
[4]刘惠敏.大型基础设施对地缘区人居环境的影响研究[J].中国人口·资源与环境,2011,21(11):139-145.[Liu Huimin.Effect Degree Modeling of Large-Scale Infrastructure to Geo-regional HumanSettlements [J]. China Population, Resources and Environment,2011,21(11):139 - 145.]
[5]Ouyang M,Dueñas-Osorio L.An Approach to Design Interface Topologies Across Interdependent Urban Infrastructure Systems[J].Reliability Engineering and System Safety,2011,96(11):1462-1473.
[6]Min H S J,Beyeler W,Brown T,et al.Toward Modeling and Simulation of Critical National Infrastructure Interdependencies[J].Iie Transactions,2007,39(1):57 -71.
[7]Torres-Vera M A,Canas J A.A lifeline Vulnerability Study in Barcelona,Spain [J].Reliability Engineering and System Safety,2003,80(2):205-210.
[8]Wang SL, HongL, ChenX G. VulnerabilityAnalysisof Interdependent Infrastructure Systems:A Methodological Framework[J].Physica A:Statistical Mechanics and its Applications,2012,391(11):3323-3335.
[9]Poljanšek K,Bono F,Gutiérrez E.Seismic Risk Assessment of Interdependent Critical Infrastructure Systems:The Case of European Gas And Electricity Networks[J].Earthquake Engineering &Structural Dynamics,2012,41(1):61-79.
[10]陈卓淳,姚遂.中国电力系统低碳转型的路径探析[J].中国人口·资源与环境,2012,22(2):62-68.[Chen Zhuochun,Yao Sui.Exploring Transition Pathways for a Decarbonized Electricity System in China-Based on the Socio-Technical Transition Approach[J].China Population,Resources and Environment,2012,22(2):62 -68.]
[11]姚保华,谢礼立,袁一凡.生命线系统相互作用及其分类[J].世界地震工程,2001,17(4):48-52.[Yao Baohua,Xie Lili,Yuan Yifan.Lifeline System Interaction and Its Classification [J].World Information on Earthquake Engineering,2001,17(4):48-52.]
[12]温瑞智,陶夏新,谢礼立.生命线系统的震害耦联[J].自然灾害学报,2000,9(2):105-110.[Wen Ruizhi,Tao Xiaxin,Xie Lili.Earthquake Damage Analysis of Coupling Lifeline Systems[J].Journal of Natural Disasters,2000,9(2):105 -110.]
[13]Rinaldi S M,Peerenboom J P,Kelley T K.Identifying,Understanding,and Analyzing Critical Infrastructure Interdependencies[J].IEEE Control Systems Magazine,2001,21(6):11 -25.
[14]Lee E E,Mitchell J E,Wallace W A.Restoration of Services in Interdependent Infrastructure Systems:A Network Flows Approach[J].IEEE Transactions on Systems,Man,and Cybernetics,Part C:Applications and Reviews,2007,37(6):1303 -1317.
[15]Benoit R.A Method for the Study of Cascading Effects Within Lifeline Networks [J]. International Journal of Critical Infrastructures,2004,1(1):86 -99.
[16]Dueñas-Osorio L,Vemuru S M.Cascading Failures in Complex Infrastructure Systems[J].Structural Safety,2009,31(2):157 -167.
[17]Ouyang M,Hong L,Mao Z J,et al.A Methodological Approach to Analyze Vulnerability ofInterdependentInfrastructures [J].Simulation Modelling Practice and Theory,2009,12(5):817 -828.
[18]张明媛,袁永博,李宏男.基于脆性理论的灾害作用下生命线系统耦联分析[J].防灾减灾工程学报,2009,29(4):462-466.[Zhang Mingyuan,Yuan Yongbo,Li Hongnan.Analysis of the Coupling of Lifeline Systems Based on Brittleness Theory Under Disaster[J]. JournalofDisasterPrevention and Mitigation Engineering,2009,29(4):462 -466.]
[19]Ge Y,Xing X T,Cheng Q M.Simulation and Analysis of Infrastructure Interdependencies Using a Petri Net Simulator in a Geographical Information System [J].International Journal of Applied Earth Observation and Geoinformation,2010,12(6):419-430.
[20]Johansson J,Hassel H.An Approach for Modeling Interdependent Infrastructures in the Context of Vulnerability Analysis [J].Reliability Engineering and System Safety,2010,95(12):1335-1344.
[21]Zhang P C,Peeta S.A Generalized Modeling Framework to Analyze Interdependencies Among Infrastructure Systems [J].Transportation Research,Part B:Methodological,2011,45(3):553-579.
[22]Herrera F,Martínez L.A 2-tuple Fuzzy Linguistic Representation Model for Computing with Words[J].IEEE Transactions on Fuzzy Systems,2000,8(6):746 -752.
[23]Gabus A,Fontela E.World Problems,an Invitation to Further thought within the Framework of DEMATEL[R].Switzerland Geneva:Battelle Geneva Research Centre,1972.
[24]Papoulis A,Pillai S U.Probability,Random Variables,and Stochastic Processes[M].New York:McGraw-Hill,2002.
