目标散布已知情况下鱼雷发现概率计算方法

于雪泳，李本昌，黄文斌

(海军潜艇学院，山东 青岛 266042)

0 引言

在目标位置散布概率密度已知的情况下，计算某种搜索行动发现目标的概率，对于搜索决策的优化具有十分重要的意义。

求解声自导鱼雷机动搜索发现目标的概率，是这类问题的一个典型实例。

1 问题的描述

目标散布概率密度已知情况下，声自导鱼雷机动搜索发现目标概率的计算，需要明确已知条件和要求解的问题。其中已知条件包括目标散布概率密度、声自导鱼雷探测手段和声自导鱼雷搜索弹道。

1.1 目标散布概率密度

目标散布概率密度表征了目标位置点在二维空间中的分布情况，在鱼雷攻击过程中，目标散布概率密度是动态的，即目标散布概率密度是时间的函数。在潜艇自行跟踪、解算目标运动要素和引导兵力通报目标信息情况下，可以求得目标散布概率密度近似符合二维正态分布，即平面直角坐标系(x，y)处存在目标的概率p(x，y)的表达式为

式中:σx为x轴方向的标准差，σx是时间的函数，即σx=σx(t);σy为y轴方向的标准差，σy是时间的函数，即σy=σy(t);r为协方差，r是时间的函数，即r=r(t)。

1.2 声自导鱼雷探测手段

声自导鱼雷通过声呐设备探测目标，为方便问题的求解，将声自导鱼雷探测能力用发现目标距离d和鱼雷搜索有效扇面角±α表示。当目标处于鱼雷搜索有效扇面之内且距离小于d时，即认为鱼雷发现目标，如图1所示。

1.3 声自导鱼雷搜索弹道

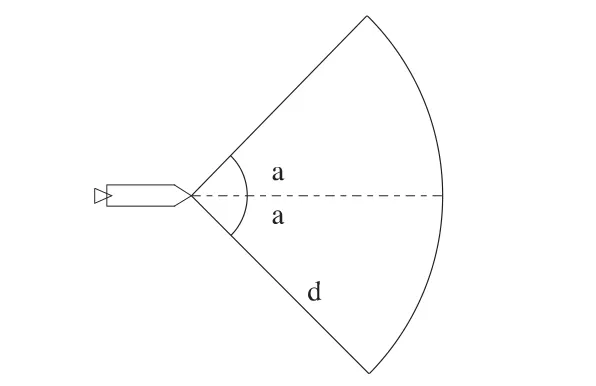
图1 鱼雷探测能力示意图Fig.1 Map of torpedo detection capacity

鱼雷机动搜索弹道是鱼雷机动过程中，按时间顺序形成的鱼雷位置点的数据序列。一般情况下，鱼雷搜索弹道不能用一个确定的函数来表达，而用鱼雷弹道仿真程序中的数值方式来描述。即

当t=t1时，x=x1，y=y1;当t=t2时，x=x2，y=y2。

1.4 要求解的问题

一般情况下，要考察鱼雷的机动搜索过程内或从开始搜索到某时刻范围内，即t［0，T］的时间范围内，鱼雷搜索到目标的概率P。

2 问题的解决思路

因已知目标散布概率密度是时间的函数，且可以用确定的函数表达，鱼雷机动搜索弹道也可以确定，要求鱼雷在时间［0，T］范围内发现目标的概率。可以考虑鱼雷在某时间段［t，t+Δt］内用鱼雷有效作用范围所经过的区域作为积分区间，用目标散布概率密度在t时刻的数值作为被积函数，用数值积分的方法求出［t，t+Δt］内鱼雷发现目标的概率。当Δt→0时，求得的发现概率为［t，t+Δt］时间段内鱼雷发现目标的概率dP(t)。对dP(t)在区间［0，T］进行积分计算，即为［0，T］时间段内鱼雷机动搜索发现目标的概率。即

在计算dP(t)的过程中，因被积函数 (即目标散布概率密度)表达式十分复杂，积分区间具有不规则性，很难用数学表达式进行描述，所以用求解积分表达式的方法进行计算是十分困难的。鉴于此，可以用计算机仿真和数值积分的方法，进行积分过程的计算。

3 问题的求解过程

要用数值积分的方法求得声自导鱼雷机动搜索［0，T］时间段内发现目标的概率，需要在合适的坐标系内，描绘鱼雷机动搜索的相对弹道，然后确定积分区域，进行数值积分计算。

3.1 鱼雷相对弹道

为便于发现概率数值积分的计算，在鱼雷机动搜索仿真程序中，引进相对弹道的概念。相对弹道是相对绝对弹道而言的。

绝对弹道就是鱼雷在机动搜索过程中，其位置点所形成的弹道。

相对弹道是鱼雷机动搜索过程中，其位置点与此时刻目标散布中心点之差所构成的数据序列形成的弹道，即

式中:x'(t)，y'(t)为鱼雷 t时刻的相对位置点;x(t)，y(t)为鱼雷t时刻的绝对位置点;X(t)，Y(t)为目标t时刻的绝对位置点。

3.2 Δt的确定

在用数值积分法计算［t，t+Δt］鱼雷发现目标概率的过程中，是以鱼雷有效作用范围所经过的区域作为积分区间，以目标散布概率密度在t时刻的数值作为被积函数的。

在数学意义上，Δt可以取无限小，计算所得的发现概率p(t)为t时刻鱼雷发现目标的即时概率。但用数值积分方法，Δt如果取得太小，就会增大计算量，影响计算速度;如果Δt取得太大，用t时刻的目标概率密度作为被积函数就会有较大误差。所以，为兼顾计算速度和计算精度，应适当选择Δt的大小。在鱼雷机动搜索过程中，由于鱼雷和目标的速度均不太高，且目标散布概率密度随时间变化不很剧烈，在实际计算过程中，取Δt=1 s就可得到较高的计算精度，且不影响计算速度。

3.3 ［t，t+Δt］内积分区域的确定

为求得［t，t+ Δt］内的数值积分，必先确定［t，t+Δt］内的积分区域。这个积分区域是鱼雷在t时刻与(t+Δt)时刻所经历的搜索区域的增量。

为便于说明和计算，设以任意时刻目标散布中心点为原点，在一定距离范围 (本例中以10 km×10 km)上标绘鱼雷相对位置点及目标散布密度图。在t时刻，鱼雷位置点及目标散布密度如图2所示。(t+Δt)时刻，鱼雷搜索范围以及搜索范围增量如图3所示。图3中“铲”形区域就是［t，t+Δt］内的积分区域。

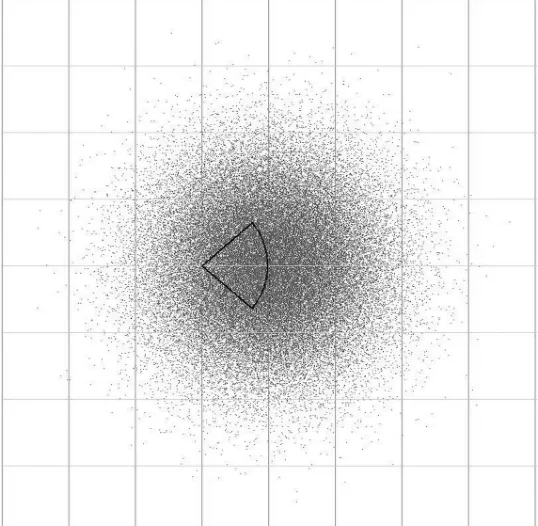
图2 t时刻鱼雷相对位置图Fig.2 Relative position of torpedo at t

图3 (t+Δt)时刻鱼雷相对位置图Fig.3 Relative position of torpedo at t+Δt

3.4 ［t，t+Δt］内的数值积分

因［t，t+Δt］内积分区域的形状具有不规则性，所以采用“图形相与”的方法进行积分计算。

所谓“图形相与”，就是以图3中的“铲”形区域所代表的图形像素，与图3所表示的范围中的对应像素处目标散布概率密度值进行“与”计算，获得［t，t+Δt］内鱼雷发现目标的概率。目标概率密度图与积分区间相“与”的效果如图4所示。

图4 积分区间和被积函数图Fig.4 Map of integral interval and integrand

图4中以色彩代表目标概率密度的数值，图形中央的“铲”形区域就是［t，t+Δt］内积分区域。图5是数值积分的立体图，目标散布概率密度呈“山丘”形状，积分区域范围内的体积，就是［t，t+Δt］内鱼雷发现目标的概率。

图5 数值积分立体图Fig.5 Three-dimension map of integral numerical integration

3.5 ［0，T］内鱼雷发现目标的概率

按3.1～3.4节的步骤，用程序的方法计算［0，Δt］，［Δt，2Δt］，［2Δt，3Δt］，…［T－Δt，T］时间段内鱼雷发现目标的概率，然后进行累加，即得到鱼雷在［0，T］时间内发现目标的概率。

4 结语

目标散布概率密度已知情况下，声自导鱼雷机动搜索发现目标概率的计算方法，可以作为规划鱼雷机动搜索弹道的手段，也可以用于鱼雷弹道的设计。这种计算方法亦可扩展应用到其他领域，如海上目标搜寻、海底沉船搜寻等，计算多种搜索方案发现目标的概率，选择发现目标概率最高的方案，以此来优化搜索行动。

［1］孟庆玉.鱼雷作战效能分析［M］.北京:国防工业出版社，2003.

［2］徐培德.武器系统分析［M］.长沙:国防科技大学出版社，2001.

［3］同济大学数学教研室.高等数学［M］.北京:高等教育出版社，1991.

［4］杨振明.概率论［M］.北京:科学出版社，1999.

［5］沈永欢.实用数学手册［M］.北京:科学出版社，2004.

［6］朱清新.离散和连续空间中的最优搜索理论［M］.北京:科学出版社，2006.

［7］周斌.基于全局概率密度搜索的快速目标跟踪［J］.电子与信息学报，2010(11):2680－2685.ZHOU Bin.Fast object tracking with global kernel density seeking［J］.Journal of Electronics ＆ Information Technology，2010(11):2680－2685.