潜艇悬停运动模糊控制
2013-08-26熊瑛,颜俐,许建
熊 瑛,颜 俐,许 建
(1.中南民族大学,湖北 武汉 430074;2.中国舰船研究设计中心,湖北 武汉 430064)
0 引言
到目前为止,几乎所有的潜艇都安装了自动操舵系统。与水面舰船不同,潜艇上的自动操舵系统不仅要控制航向,而且要控制深度和纵倾。由于大多数潜艇的自动舵都采用PID舵,而常规的PID自动舵是基于潜艇运动的数学模型设计的,其模型越精确,响应就越好。而潜艇运动系统是一个大惯性、非线性、环境干扰复杂的系统,难以用一个精确的数学模型来描述。即便是目前世界上普遍采用的用于潜艇仿真模拟的标准六自由度运动方程,与潜艇的真实运动也存在着一定的差异,而且方程中的水动力系数的获得也非常困难。模糊控制正是一种特别适用于那些难以用精确数学模型描述而主要依赖于人工经验的系统。目前,人们已经将模糊控制应用到水面船舶操纵控制中,但仅仅限于航向模糊控制,用于潜艇悬停控制的模糊控制器还很少涉及。本文将根据潜艇悬停控制的特点,提出潜艇悬停运动模糊控制的方法,为水下悬停的自动操纵控制提供了初步的技术基础。
1 潜艇悬停模糊控制器的设计
1.1 潜艇水下悬停运动的系统模型
悬停是潜艇水下重要停泊方式之一,是指潜艇水下航行状态停车后,经准确均衡,利用专用压载水舱的注、排水,实现潜艇无航速下深度控制的操艇方式。严格意义下的悬停是潜艇对于海底相对静止的一种运动状态,而通常所说的悬停是指一般意义的悬停,是指潜艇螺旋桨的停转,保持与海水的相对静止,主要任务是保持悬停深度和动平衡。潜艇进行悬停可有效降低潜艇噪声,提高隐蔽性,增大目标探测距离;减少用电量,延长充电间隔时间,增加水下潜航时间;悬停操纵时潜艇的机动性较好[1-6]。
潜艇水下悬停运动的系统模型如图1所示,该模型有3个初始干扰输入,分别为艇体压缩、初始不均衡量和海水密度变化,这些干扰加在悬停运动模型上,使运动模型的运动状态发生改变,通过把深度偏差和深度偏差变化率输入到悬停模糊控制器,得到相应的控制量,从而启动悬停水舱进行注排水操作,直到实际深度与指定深度一致为止。
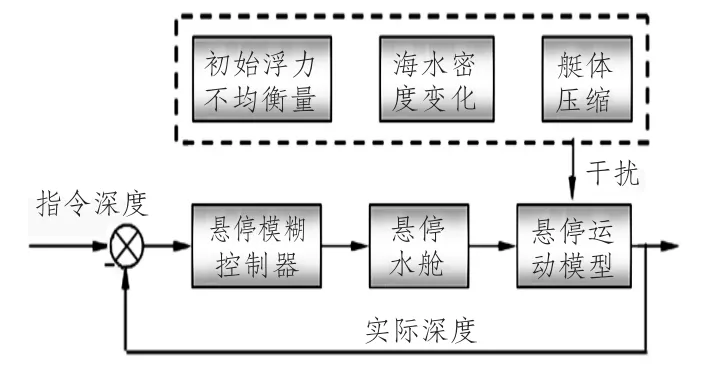
图1 潜艇水下悬停运动的系统模型Fig.1 System model of submarine hovering
1.2 悬停模糊控制器的结构
模糊控制系统的组成与一般的计算机控制系统相似,唯一不同之处是控制装置由模糊控制器来实现。一般来说,模糊控制器主要由模糊化、知识库、模糊推理、反模糊化这4个主要的功能模块组成[7-11]。模糊控制器结构如图2所示。
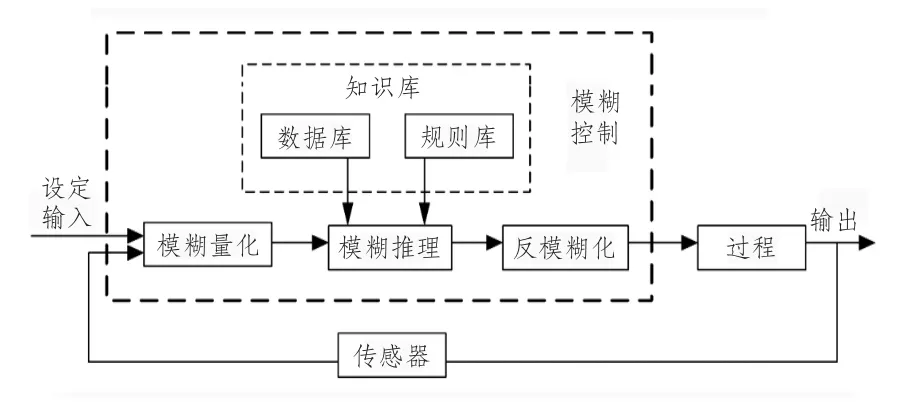
图2 模糊控制器结构图Fig.2 Fuzzy controller structure
因为模糊控制器的输入输出都是非模糊量,而其内部却建立在语言型的模糊控制率上,由条件满足的程度用模糊推理推出模糊输出的大小。所以为了进行模糊推理必须将非模糊量转化为模糊值,即模糊化。由于模糊推理的输出是模糊值,还必须将模糊输出转化为非模糊集,即反模糊化。模糊控制器的模糊化、模糊推理及反模糊化共同建立在知识库的基础上。知识库由数据库和规则库2部分组成。数据库存放所有输入、输出变量的全部模糊子集的隶属度矢量值或隶属度函数。规则库是基于专家知识或手动操作熟练人员长期积累的经验,它以“If-Then”的语言形式表示,构成模糊控制规则。模糊控制规则和隶属函数及推理方法共同决定模糊控制器的传递特性。
1)模糊化
对于一个实际的被控过程,模糊控制器的输入总有一个最大变化范围,这个范围称作外部输入论域,而在定义模糊推理所采用的语言变量 (即模糊子集)时,还要规定一个内部输入论域。模糊化单元的任务就是要实现这种论域的转换,同时还要为语言变量赋值,即模糊化。
在潜艇悬停运动模糊控制器中,模糊化的具体过程如下:
①首先将潜艇深度偏差e和深度偏差变化率ec作为输入量,将注排水量作为输出量;然后将这些输入输出量作为模糊控制器的输入输出语言变量。
②在潜艇悬停运动时,设定深度偏差e的基本论域为[-5,5],m;深度偏差变化率ec基本论域为[-1,1],m/s;注排水量 u基本论域为[-2000,2000],L。
③将已经变化到论域范围的输入输出量进行模糊处理,使精确的输入输出量变成模糊量,并用相应的模糊集合来表示。
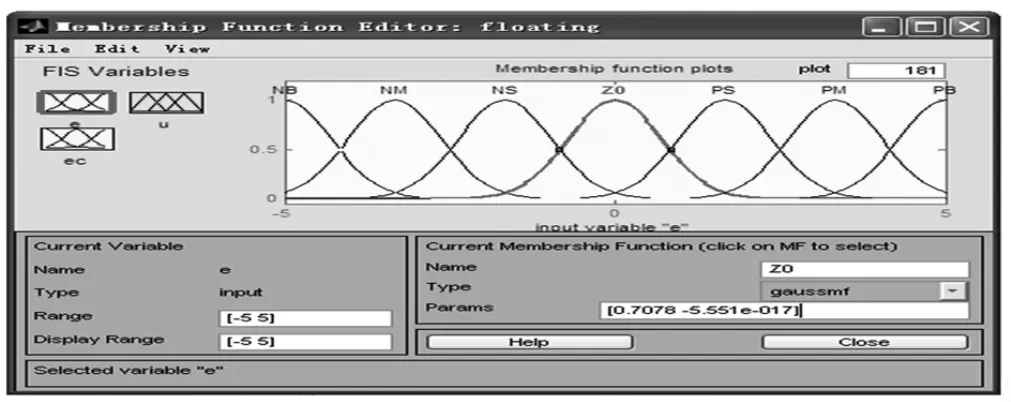
图3 输入e的隶属度函数Fig.3 Membership function of input e
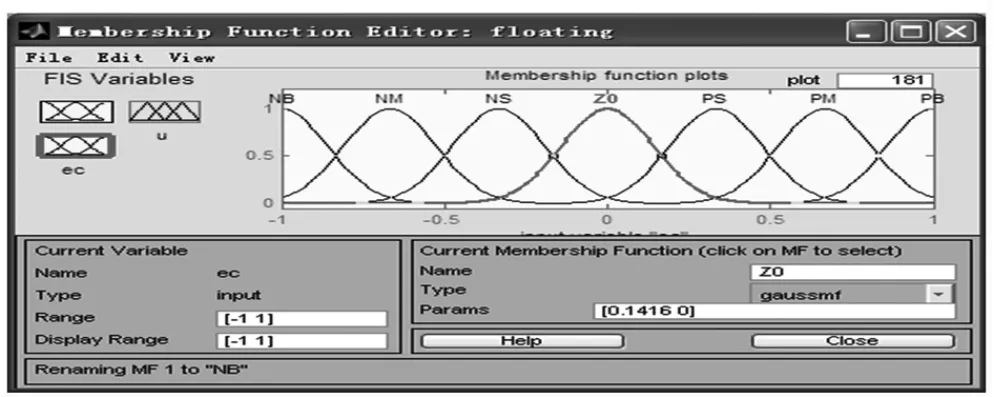
图4 输入ec的隶属度函数Fig.4 Membership function of input ec
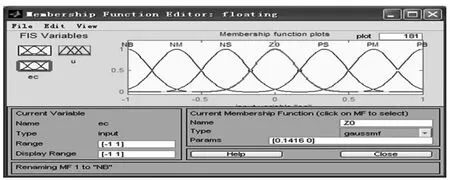
图5 输出u的隶属度函数Fig.5 Membership function of output u
输入、输出的隶属度函数曲线如图3~图5所示。在潜艇悬停运动模糊控制中,各语言变量的语言值均取为“负大”(NB),“负中”(NM),“负小”(NS),“零”(ZO),“正小”(PS),“正中”(PM),“正大”(PB)共7种。根据上述原则,隶属度函数选用高斯型函数,宽型隶属函数反映模糊集合具有低分辨率特性,误差控制的灵敏度较低,控制特性比较平缓,所以选取较宽的隶属度函数。相邻的隶属度函数之间有部分重叠,间隔的没有交叉越界。
2)知识库
知识库包含了具体应用领域中的知识和要求的控制目标,它通常由数据库和模糊控制规则库2部分组成。数据库主要包括各语言变量的隶属度函数、尺度变换因子以及模糊空间的分级数等。规则库包括了用语言变量表示的一系列控制规则。它们反应了控制专家的经验和知识。规则库中存放着全部模糊控制规则,在模糊逻辑推理时为模糊推理机提供控制规则。语言变量的模糊子集划分越细,规则条数就越多。若能保证专家知识的准确度,那么规则条数越多,规则库的准确度就越高。基于图6的性质,可以得到如表1所示的模糊控制器控制规则。
图6描述了潜艇悬停过程的典型阶跃响应。刚开始时,即在a点附近,深度偏差e很大,而深度偏差变化率ec很小,这时主要是为了消除深度偏差,因此需要加大注水量使潜艇快速变深以减小偏差。所以在a点附近的规则为:如果深度偏差e是PB且ec是ZO或NS,则注排水量为NM。
在b点附近,深度偏差e很小,而偏差变化率ec比较大,这时要防止系统产生超调甚至振荡,需要一个正小的控制信号以避免实际深度超调过大。因此,在b点附近的规则为:如果深度偏差e是ZO且ec是NB,则注排水量为PS。
在点c和d附近的控制行为分别与点a和b附近的相似。利用这样的思路可以总结出悬停控制器的模糊规则:当e较大时,应当采取加大注排水量,为了快速消除深度偏差,此时深度偏差e在控制器中占主导地位;当e中等大小时,为防止较大超调,应适当减小注排水量以免产生较大的超调;当e较小而ec较大时,偏差很小而主要任务是防止大的超调或是振荡,此时ec占主导地位,应进行反向注排水。

图6 悬停控制过程的典型阶跃响应Fig.6 The classic step response of hovering control
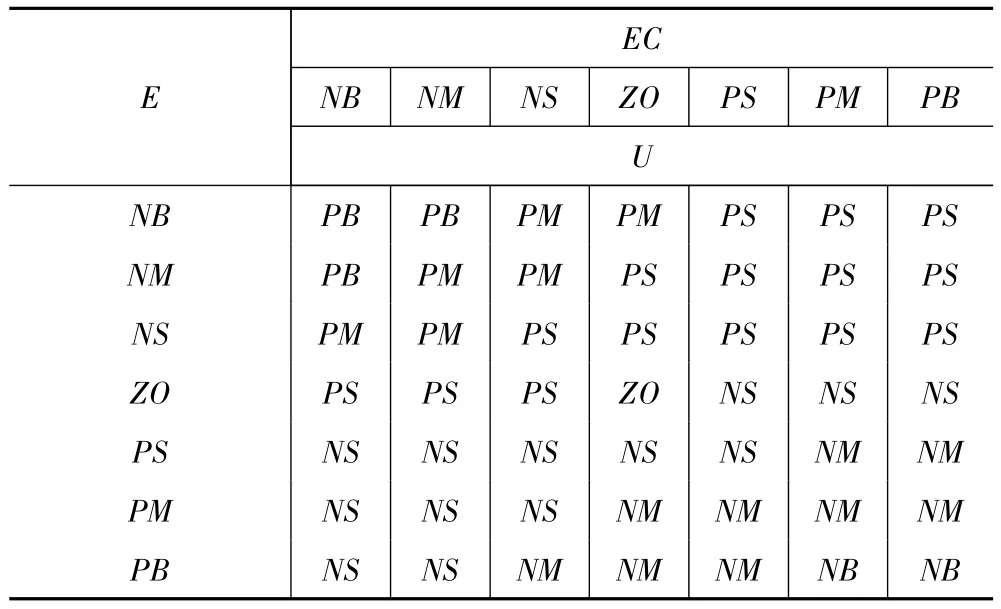
表1 控制规则Tab.1 Control rule
3)模糊推理
模糊推理是模糊控制器的核心,它具有模拟人的基于模糊概念的推理能力。该推理过程是基于模糊逻辑中的蕴含关系及推理规则来进行的。按控制量的计算方法可分为以下2类:
①在线计算方法
这种方法是在系统控制过程中按控制规则,由被测过程量在线计算出响应的控制量。
②查表计算法
这种方法是根据模糊控制规则事先离线计算出过程量在各种情况下的一组控制量,形成模糊控制表。在整个控制过程中,控制量的计算就转化为直接查找被测过程量的控制表。
在悬停控制器中,根据输入变量深度偏差和深度偏差变化率,经过控制规则表1来推导出输出变量排注水量。
利用Matlab模糊工具箱可以看到各语言变量的模糊推理特性曲面。从图7可以看,出e,ec和u的模糊推理输出特性曲面过渡平滑,没有突变。由此可知,悬停控制器的模糊控制规则选择合理。
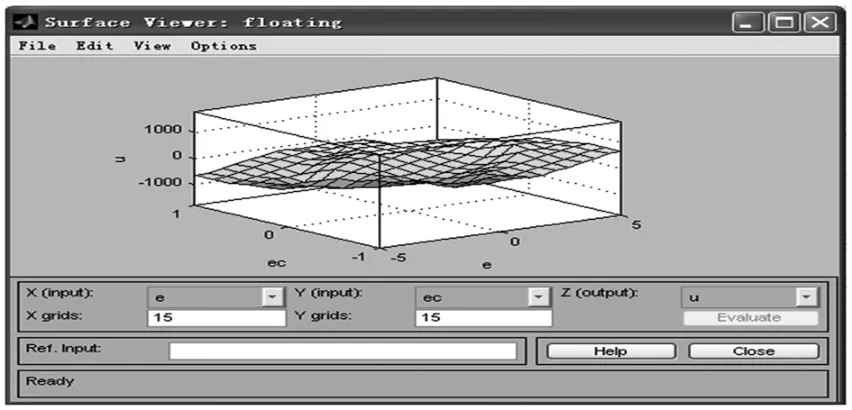
图7 e,ec和u的模糊推理输出特性曲线Fig.7 Fuzzy reasoning curve of e,ec and u
4)反模糊化
通过模糊推理得到的是模糊量,而对于实际的控制必须为非模糊量即清晰量,因此需要将模糊量转换成清晰量,并将表示在论域范围内的清晰量经尺度变换变成实际的控制量。将模糊的控制量经清晰化计算变换成表示在论域范围内的清晰量,通常有最大隶属度法、中位数判决法和面积中心法几种方法。
上述3种方法各有优缺点,最大隶属度法简单易行、使用方便、实时性好,但是利用的信息很少;中位数判决法利用信息太多,计算量很大;面积中心法不仅有公式可循,利用信息较多,实际应用比较广泛,所以本论文采用面积中心法进行模糊决策。
2 自抗扰跟踪微分器的设计
悬停模糊控制器选用二维的模糊控制器,控制器的输入有深度偏差e和深度偏差变化率ec。深度偏差变化率是一个微分信号,而潜艇的深度偏差变化率不能直接通过传感器得到,只能通过深度偏差微分得到数字量,因此要得到微分量还需要加入微分器。在经典调节理论中,采取直接微分的方式得到深度的一阶微分量,也是常用的处理方法之一。但经典微分器在微分被随机信号污染时就会出现放大污染噪声,从而使出来的微分信号产生毛刺和抖动。通过数学推导可以得到,输出信号y(t)是输入信号v(t)的微分信号叠加上放大了1/T倍的噪声信号,由于时间常数T很小,噪声放大很严重,有时完全可以淹没微分信号,所以经典微分环节会产生对噪声的严重放大效应。因此,在微分处理过程中要避免将一个状态变量微分产生另一个状态变量。
从图8可以看出,经典微分器输出的微分信号抖动非常明显甚至失真,最速非线性跟踪微分器[12]输出的微分信号非常平滑,由于上述原因,本文将采用最速非线性跟踪微分器得到深度的微分信号,从而在很大程度上提高模糊控制器的控制效果。
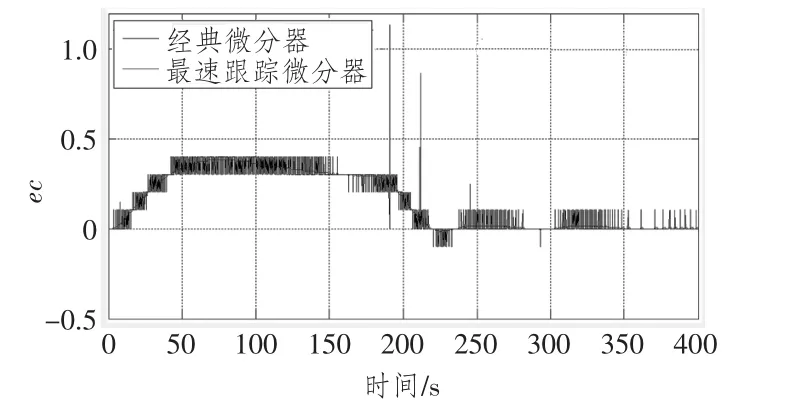
图8 两种微分器的信号比较Fig.8 Signal comparison of two differentiators
最速控制综合函数为 fhan(x1,x2,r,h),其表达式如下:
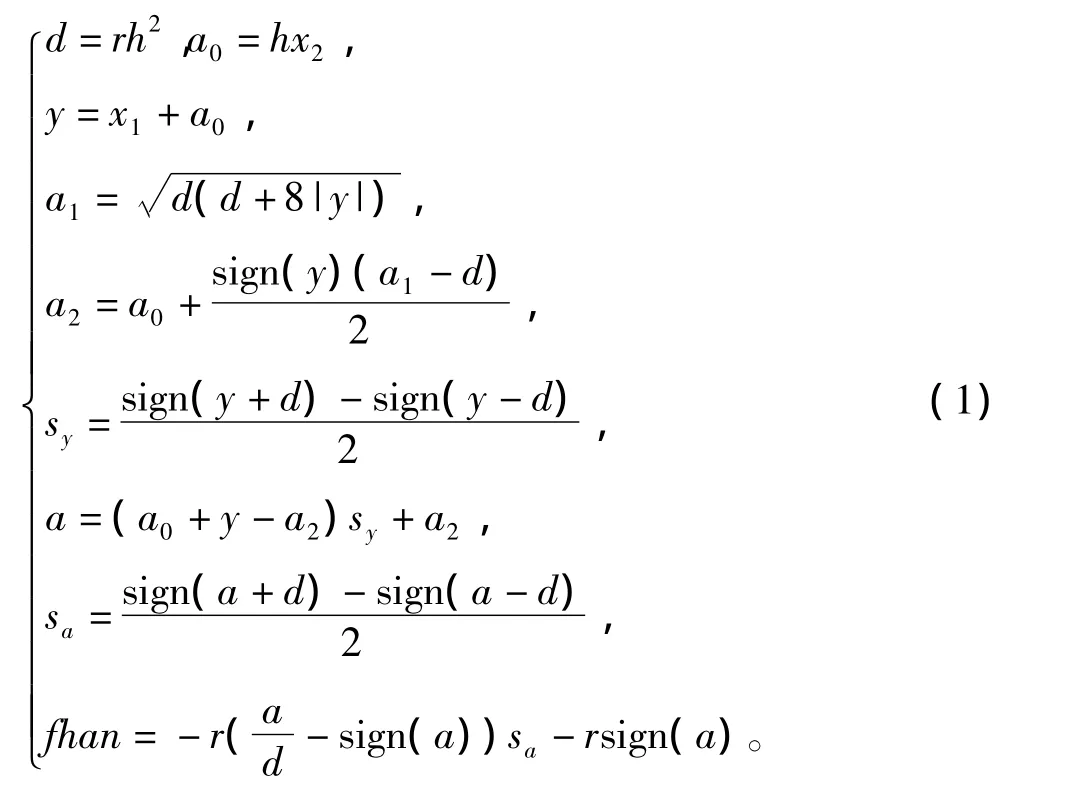
设二阶离散系统为
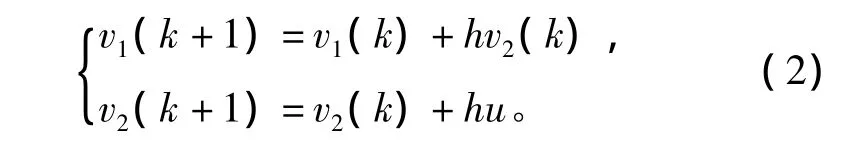
利用最速综合函数 fhan(x1,x2,r,h)建立的离散最速反馈系统为
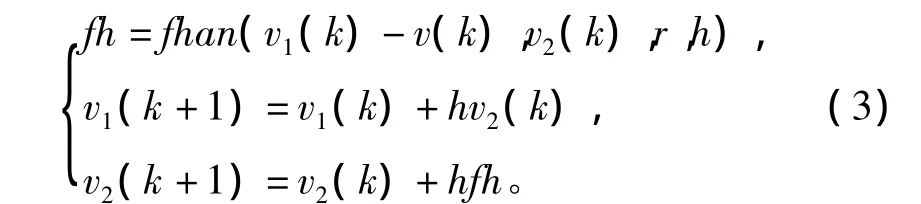
系统(3)是很好的数值微分器,称作“快速离散跟踪微分器”。将函数fhan(x1,x2,r,h)中的步长 h改成与系统步长独立的参数h0,把它用于信号处理将有很多特殊的功能。这时把参数r称作“快速因子”,而把参数h0称作“滤波因子”,此时跟踪微分器变为
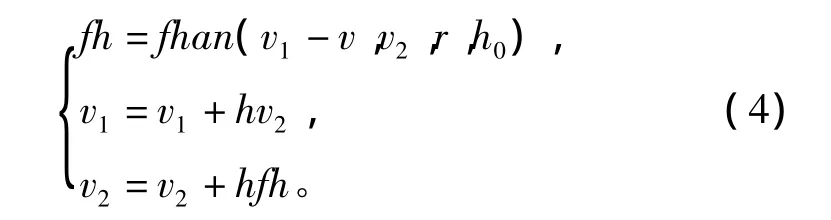
输入信号v(t)时,v1(t)跟踪输入信号,v2(t)是v1(t)的微分信号,当作输入信号v(t)的微分近似。
自抗扰跟踪微分器就是一个信号处理环节,实现了对输入信号过渡过程的安排及微分信号的提取。自抗扰跟踪微分器给出了闭环系统一种可以实现的动态性能指标,这种给定对于被控对象来说不再是一种稳态的期望值,而是一种可实时跟踪的曲线。同时,在输入信号存在外界扰动时,自抗扰跟踪微分器还可以实现滤波的作用。
3 系统仿真验证
利用Simulink仿真模块建立潜艇水下定深悬停模糊系统模型。
其中ADRCTD模块由二阶离散跟踪微分器的s函数完成,Hover模块由潜艇水下悬停运动数学模型的s函数完成。系统仿真连接如图9所示。
选取2种典型的工况进行仿真,证明模糊控制在理论上的可行性。仿真结果如图10~图13所示。

图9 悬停仿真图Fig.9 Simulation of hovering
1)干扰为正梯度条件下,初始不均衡量为艇重300 L,初始不平衡力矩对应的移水量为200 L,初始偏差为2 m。
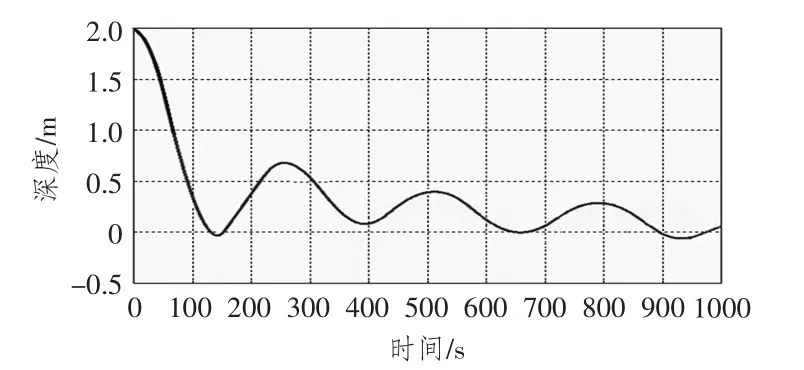
图10 深度变化曲线Fig.10 Curve of depth variation
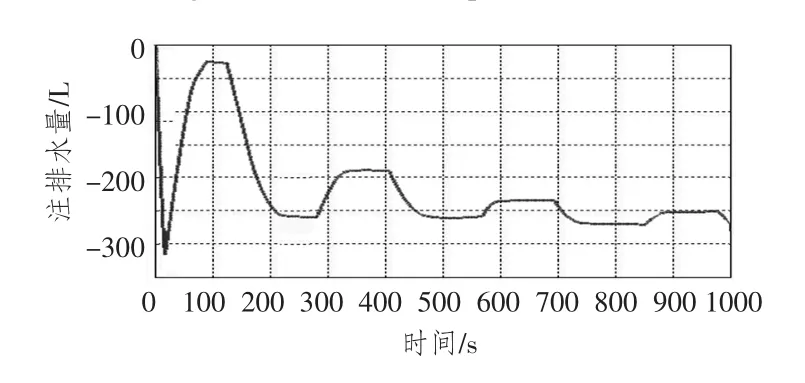
图11 排注水曲线Fig.11 Curve of drainage and injection
2)干扰为负梯度条件下,初始不均衡量为艇重300 L,初始不平衡力矩对应的移水量为200 L,初始偏差为2 m。

图12 深度变化曲线Fig.12 Curve of depth variation
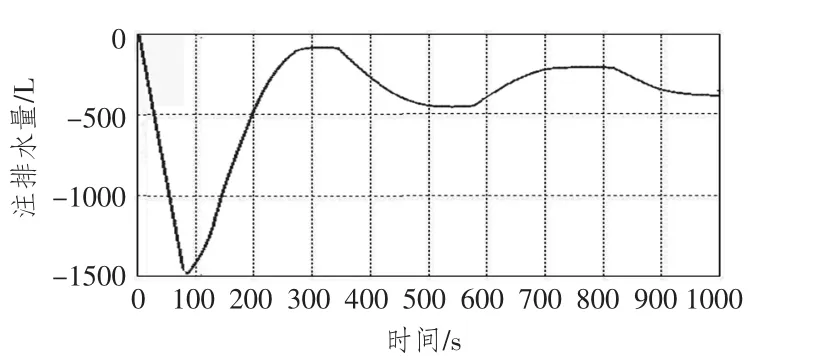
图13 排注水曲线Fig.13 Curve of drainage and injection
4 结语
通过仿真可知,在潜艇定深悬停模糊控制中,深度变化不超过4 m,稳定后能在指定深度附近波动,符合控制要求。
海水密度正梯度变化层进行悬停操纵相对容易,因为密度变化引起的浮力变化可以平衡艇体压缩引起的浮力变化,潜艇能很快达到新的平衡状态,悬停期间注排水次数不多,注排水量不大。而在海水密度为负梯度变化层,由于艇体压缩加剧了潜艇的运动,因此在进行悬停操纵时,必须增加注排水次数,并且在深度稳定控制期间还要进行连续注排水控制,以抵消负梯度带来的干扰力影响。
采用潜艇定深悬停模糊控制方法,悬停泵排注水可实现自动控制,从而使排注水曲线表现为光滑曲线,其次控制的灵敏度有所提高,可实时根据艇体姿态改变注排水量,同时也减小了艇员操艇强度。
[1]施生达,戴余良.潜器水下悬停运动数学模型[R].武汉:海军工程大学,2006.
[2]施生达.潜器操纵性[M].北京:国防工业出版社,1995.
[3]赵小军,林莉,李明,等.基于模糊控制的潜器悬停系统[J].舰船科学技术,2007,29(4):114 -116.ZHAO Xiao-jun,LIN Li,LI Ming,et al.Hovering system based on fuzzy control[J].Ship Science and Technology,2007,29(4),114 -116.
[4]龙建军,吴百海,肖体兵.小型潜器悬停控制的建模与辨识[J].机床与液压,2008,36(8):201 -203.
[5]潘国良.潜器水下悬停运动的操纵控制研究[D].南京:东南大学,2005.
[6]潘国良.潜器悬停及其发展综述[R].中国造船工程学会2006年船舶通讯导航学术会议,2006.
[7]朱彤.PID——模糊控制的应用探讨[J].电气传动自动化,2002,24(3):11 -13.
[8]楼顺天.基于MATLAB的系统分析与设计——模糊系统[M].西安:西安电子科技大学出版社,2001.
[9]何平,王鸿绪.模糊控制器的设计及应用[M].北京:科学出版社,1997.
[10]王立新.模糊系统与模糊控制[M].北京:清华大学出版社,2003.
[11]宋彦国,张呈林.一种基于模糊控制的直升机姿态控制器设计方法[J].南京航空航天大学学报,2003,35(3):259-263.
[12]黄一,张文革.自抗扰控制器的发展[J].控制理论与应用,2002,19(4):485 -492.HUANG Yi,ZHANG Wen-ge.Development of active disturbance rejection controller[J].Control Theory &Applications,2002,19(4):485 -492.
