粘性土坝漫顶溃坝数值模型研究

姚 朗

(三峡大学科技学院，湖北宜昌 443002)

0 引言

水库大坝的修建为人类带来了巨大的经济效益和社会效益，如防洪、发电、灌溉等，然而一旦溃坝将产生巨大的危害。尤其从1958年大跃进开始到20世纪70年代中期，我国各地掀起建坝高潮，高坝大库不断出现，但与此同时，也出现了一部分“三边”工程，导致现今存在大量病险库坝。根据水利部门的水库统计，截止2002年，病险水库占水库总数的30%～40%，数量仍然较大［1］。有些水库位于城市和人口密集地区河流的上游，特别是小型水库分布广，遍布全国各地，尤其是铁路沿线交叉河流上游的小型水库。国内外已经进行了一系列土石坝漫顶溃坝机理研究的现场或室内试验［2-4］，本文建立基于溃坝机理的数值模拟，为建立溃坝灾害预警体制提供了前提条件。

1 溃口发展模拟

1.1 溃口连续冲刷扩展

水流在漫顶之后，由于水流的连续冲刷，首先在坝体下游坡面中线处产生矩形冲槽，输沙公式选择的合理性将大大影响下游坡面冲槽冲刷变化计算的准确性。

采用 Smart［5］输沙公式计算坝体冲刷率 qb，即:

其中，qb为单宽输沙体积，m2s;φ为无量纲的输沙率;g为重力加速度;s为泥沙密度与水密度的比值;d为平均粒径，mm。

根据计算出的单宽输沙体积及坝顶溃口与下游坡面冲槽的形状关系，计算Δt时间内坝体下游坡面冲槽连续冲刷深度ΔD2、溃口底部宽度变化ΔBm及溃口顶部宽度变化ΔBn(见图1，图2)。

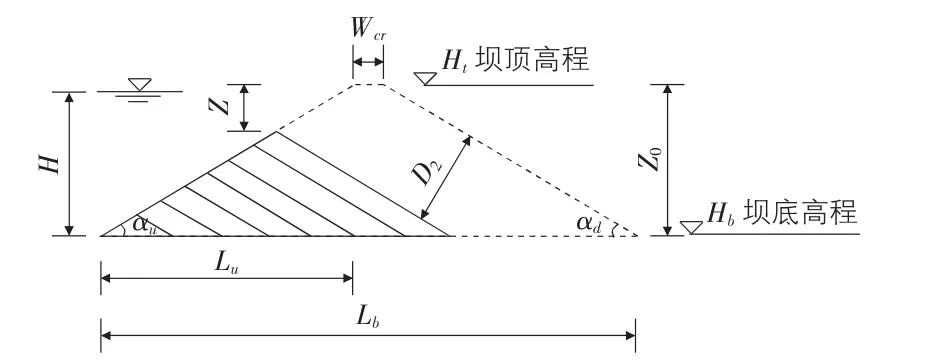
图1 溃口及冲槽示意图

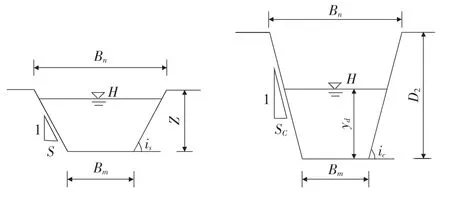
图2 坝顶溃口与坝体下游坡面冲槽图

1.2 溃口边坡间断坍塌扩展

在溃口不断加深加宽的同时，由于水流和坝体土体性质的影响，溃口边坡将可能失去稳定，发生间断性坍塌。选择合适的方法判断粘性土坝溃口边坡的稳定性，并模拟溃口边坡间断坍塌，将进一步精确溃口的发展变化过程，使计算流量更加准确。溃口边坡失稳坍塌与河岸坍塌具有一定相似性，均与水流及土体自身性质有关。借鉴Darby［6］粘性河岸稳定分析模型的原理，针对粘性土坝溃口边坡的特殊性加以改进，分析溃口边坡稳定，模拟溃口边坡间断性坍塌扩展，更加提高了模拟粘性坝体的溃口边坡间歇性坍塌现象的准确性。

考虑破坏土体上的各个作用力，采用安全系数进行判定分析溃口边坡的稳定性(见图3)，安全系数的计算公式如下:

其中，Fs为安全系数;FD为破坏面的滑动力，N/m2;FR为破坏面的滑动阻力，N/m2。

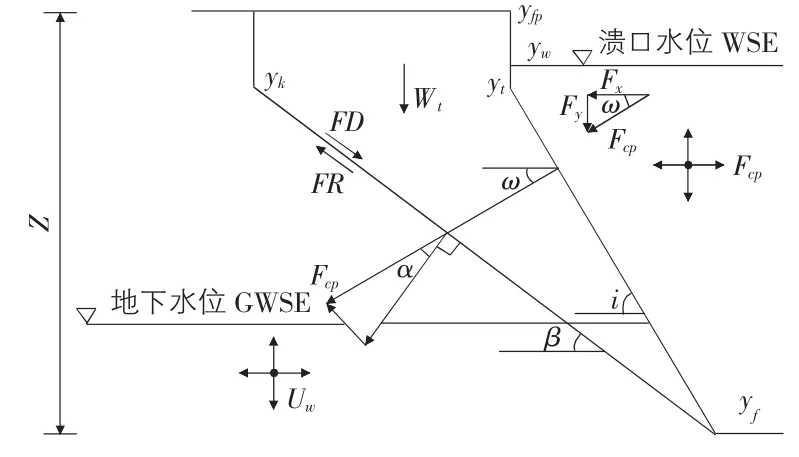
图3 垂直水流方向溃口边坡稳定分析

2 溃坝流量过程数值模拟

2.1 溃坝流量

室内试验与现场观测研究成果表明，漫顶溃坝初期，溃口出流可以用宽顶堰公式进行模拟。模型假设初始溃口形状为矩形，则溃口流量Qb为:

其中，Hc为溃口底部高度，m。随着溃口的发展，由于溃口边坡土体坍塌，溃口断面由矩形变为梯形，则溃口流量Qb为:

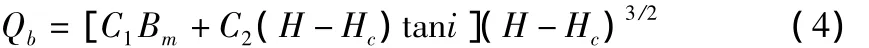
坝顶溃口以外部分，由于漫顶导致的部分流量Q0为:

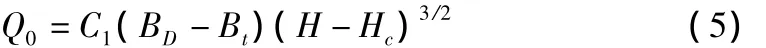
其中，C1，C2分别为矩形，三角形流量修正系数。

2.2 坝顶溃口流量修正

2.2.1 坝下游冲槽水流深度

由于溃口冲槽长度较短，冲槽的坡度较陡，可将冲槽中的水流简化为准稳态均匀流。运用曼宁公式计算冲槽中的流量为:

其中，A为断面过水面积，m2;P为湿周，m;n为糙率。

当溃坝初期溃口为矩形时，由于冲槽中的水深较浅，近似假定水力半径等于水深，则可得到冲槽中的水深yn如下:

其中，B0为溃口宽度，m。

图4 数值模型计算步骤

溃口在进一步冲刷之后，不断加深加宽，并且溃口边坡发生坍塌，之后，冲槽断面由矩形变为梯形，采用Newton-Raphson迭代法［7］计算水深 yn。

尾水对水流的淹没影响系数计算如下:

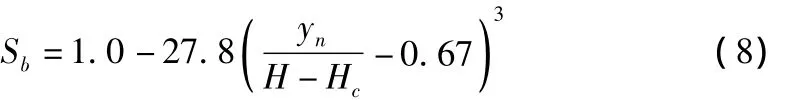
修正溃口流量如下:

其中，Sb为淹没影响系数。

2.2.2 水库水位变化

水库中的水量近似估计为:

其中，V为库容，m3;As(H)为水库的水面面积，m2;H为水面高程，m。应用质量守恒定律来计算入库流量、溃口流量、溢洪道出流量、坝顶漫流和水库蓄水特征值的影响所引起的水库水位高程(H)的变化。在一个时间步长内的质量守恒表达式为:

3 数值模型计算步骤

本文粘性土坝漫顶溃坝数值模型采用迭代计算方法求解，根据以上粘性土坝漫顶溃坝的计算理论编制程序，计算得出其溃口流量过程及上游水位过程。具体计算步骤如图4所示。

4 实例验证

板桥水库［8］是20世纪50年代初期，在淮河流域治理中最早兴建的一批综合利用的大型水利工程之一，1975年8月8日溃决。

图5 坝前水位变化曲线

计算结果显示:坝前水位过程(如图5所示)与实测情况符合较好;比较溃坝流量过程(如图6所示)，由于在数值模型中假设下游坡面冲槽发展到坝顶上游边缘之前，溃口底部高程为坝顶高程不变，使前期溃坝流量比实测值偏小，但从其中的两个关键要素(洪峰流量及出现时间)可以得到，最大溃坝流量为77 799 m3/s，与实测流量值的偏差仅为0.3%，小于5%，计算结果比较合理，计算最大溃口流量在溃坝发生后约169 min出现，计算的峰值流量到达时间比实测值略早，是由于在数值模型计算中假设在计算初始时刻已经存在初始冲槽造成的;溃口顶宽最大值为376.0 m，与实测溃口顶宽的偏差为1.1%，小于5%，底宽最大值为210.0 m，与实测溃口形状相符(如表1所示)。表明此粘性土坝漫顶溃坝数值模型能合理模拟其溃口变化过程及溃口流量过程。

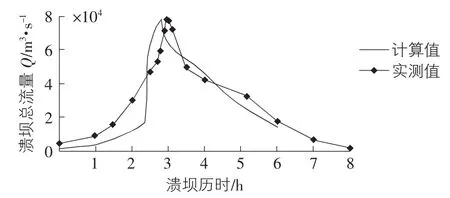
图6 溃坝流量过程曲线

表1 板桥溃坝观测值与计算值比较表

5 结语

在BREACH和BEED溃坝数值模型基础上加以改进，建立粘性土坝漫顶溃坝数值模型，计算结果较好，为建立溃坝灾害预警体制提供了可靠的前提条件。但由于粘性土坝漫顶溃坝过程复杂，仍然存在一些问题有待进一步研究，主要有以下几个方面:1)在溃口发展模拟中，假设下游坡面冲槽发展到坝顶上游边缘之后，溃口底部才开始下降，使溃口前期的流量略小，实际在前期冲刷时溃口底高已经有所下降，如何模拟这种下降过程还需要进一步研究。2)近期粘性土坝漫顶溃坝现场及室内试验中揭示了粘性均质坝“陡坎式”移动溃坝机理，并进行了粘性土均质坝“陡坎”移动速度试验研究陡坎移动速度的影响因素，将此机理运用于数值模型中将使溃口发展更加准确。3)进一步将植被覆盖体对水流的影响考虑到粘性土坝漫顶溃坝数值模型中，更加准确地模拟坝体下游坡面存在植被的大坝漫顶溃坝过程。

［1］吴中如.中国大坝的安全和管理［J］.中国工程科学，2000，2(6):36-39.

［2］周克发，李 雷.我国已溃决大坝调查及其生命损失规律初探［J］.大坝与安全，2006(5):14-18.

［3］朱勇辉，廖鸿志，吴中如.土坝溃决模型及其发展［J］.水力发电学报，2003(2):31-38.

［4］朱勇辉，廖鸿志，吴中如.国外土坝溃坝模拟综述［J］.长江科学院院报，2003(2):26-29.

［5］SMART G.M.Sediment Transport Formula for Steep Channels［J］.Journal of Hydraulic Engineering，1984(110):267-276.

［6］DARBY S.E.Development and Testing of Riverbank-stability Analysis［J］.Journal of Hydraulic Engineering，1996(122):443-454.

［7］MATHEWS JOHN H.，D.FINK KURTIS.Numerical Methods Using MATLAB Fourth Edition［M］.BEIJING:Publishing House of Electronics Industry，2005.

［8］汝乃华.大坝事故与安全·土石坝［M］.北京:中国水利水电出版社，2001.