静电场边值问题的一个教学案例

崔 翔

(华北电力大学电气与电子工程学院，北京 102206)

“电磁场”课程是高等学校电气工程及其自动化等本科专业学生必修的一门重要基础课程。电磁场仿真软件包已经成为学生毕业后解决工程电磁场问题的主要工具。因此，在“电磁场”课程的教学过程中，培养学生对工程电磁场问题的数学抽象及其边值问题的正确描述的能力，已经成为很多教师的共识［1］。现在，随着笔记本电脑在学生中的广泛普及，越来越多的教师开始尝试鼓励学生应用电磁场仿真软件包分析典型的工程电磁场问题，以提高学生学习“电磁场”课程的兴趣，加深对基本概念和基本理论的理解。

笔者在“电磁场”课程讨论课上使用过一个静电场边值问题的教学案例，课堂讨论表明，通过这个教学案例，可以全面地训练学生对静电场边值问题的数学抽象及其正确描述的能力。

1 教学案例

图1为一个三相电力汇流排的截面示意图［2］，场域Ω的结构对于图中的虚线Ss对称。设其在纵向方向无限长，汇流排内介质为空气且无空间电荷，汇流排外框S0接地，三个矩形截面导体与工频三相对称电压源联接，其相电压分别为

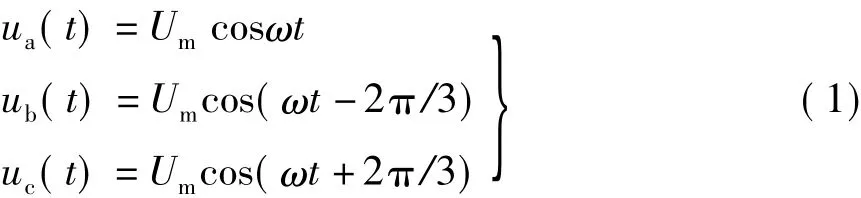
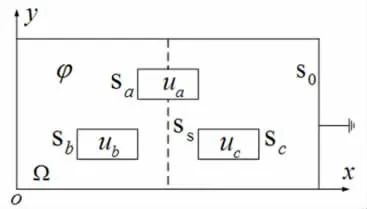
图1 三相电力汇流排的截面图

试分别讨论如下五种情况下对应的静电场边值问题，并要求计算代价尽可能低(如在相同计算精度下计算规模尽量小等):①ωt+π/2;②ωt=π;③ωt任意;④导体Sa电位悬浮且其上单位长总电荷为0;⑤导体Sa电位悬浮且其上单位长总电荷为Q0。

显然，图1是一个电准静态场问题，即导体施加电压源后其上电荷产生的库仑电场远远大于磁场变化产生的感生电场。所以，电位函数在场域中满足的边值问题与静电场边值问题相似。对于案例前三个问题，电位函数在任意时刻t满足的边值问题为

如果不考虑计算代价尽可能低的要求，案例前三个问题并无本质区别。然而，我们不妨向学生提问，能否利用图1所示场域Ω结构上的对称性来降低上文②的计算代价?并为此展开讨论。

2 电位给定导体问题

［讨论1］:在 t=π/2ω 时刻，即 ωt=π/2相位时，ua=0，ub=-uc=0.866Um，如图 2(a)所示。此时，电位函数关于虚线Ss呈奇对称分布，即在图2(a)Ω域中任意一点的电位与虚线Ss对称点的电位大小相等，极性相反。如图上两个对称方框所示，而虚线Ss上的电位为0。因此，只要分析虚线Ss左侧或右侧一半场域Ω0.5的静电场边值问题就可以了，另一半场域内的电位函数可以直接通过奇对称性质获得。至此，图2(a)全场域就可以简化为图2(b)半场域的静电场边值问题，并取虚线Ss为第一类边界且电位为0。式(2)可以改写为

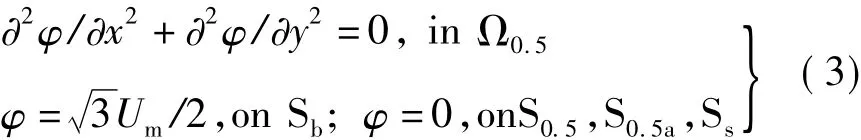
图2(c)给出了通过半场域计算后获得的全场域的电位分布图。显然，图2(b)半场域的静电场边值问题的计算代价要比图2(a)全场域的计算代价低得多。

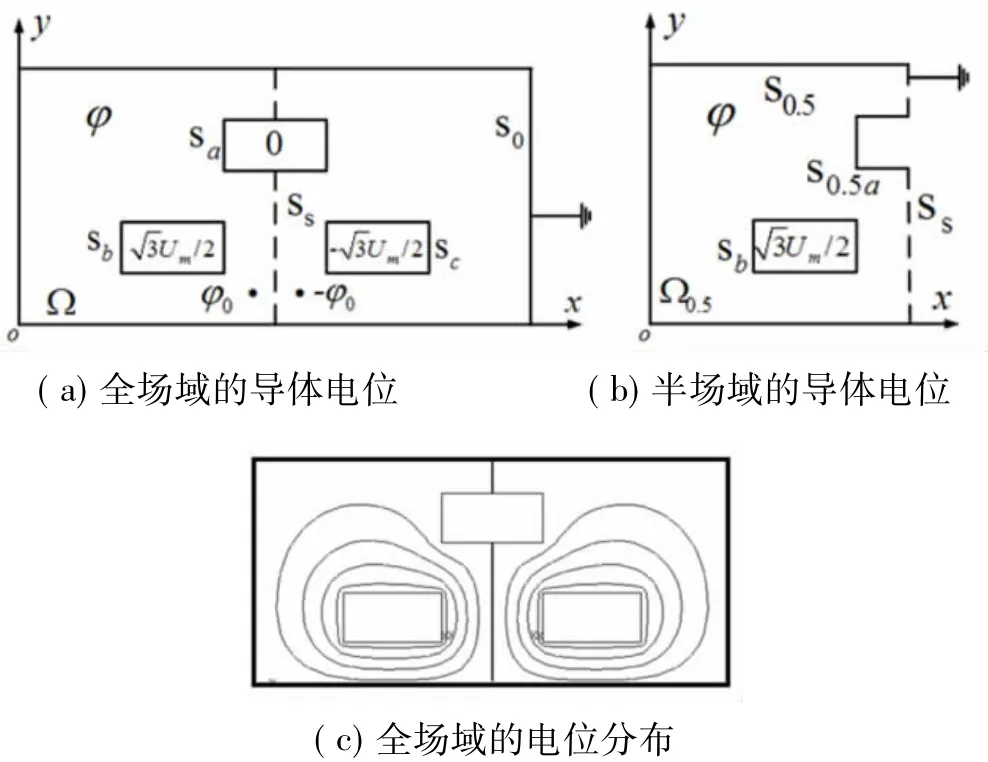
图2 ωt=π/2时三相电力汇流排的电位分布

［讨论2］:在t=π/ω时刻，即为ωt=π相位时，ua=-Um，ub=uc=0.5Um，如图 3(a)所示。此时，电位函数关于图3(a)虚线Ss呈偶对称分布，即在图上Ω域内任意一点的电位与虚线Ss对称点的电位大小相等、极性相同，如图3(a)两个对称点方框所示，而在虚线Ss上电位函数的法向偏导数为0。因此，只要分析虚线Ss左侧或右侧一半场域Ω0.5的静电场边值问题就可以了，另一半场域内的电位函数可以直接通过偶对称性质获得。

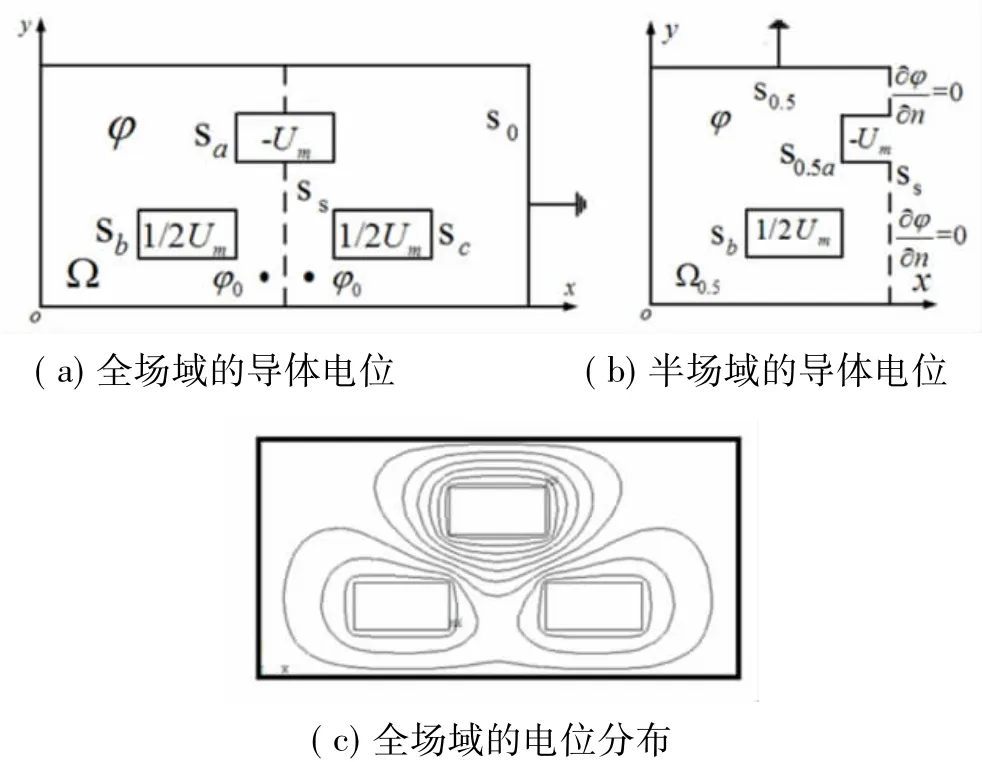
图3 ωt=π时三相电力汇流排的电位分布

至此，图3(a)全场域就可以简化为图3(b)半场域，并取虚线Ss为第二类边界且电位函数的法向偏导数为0。式(2)可以改写为

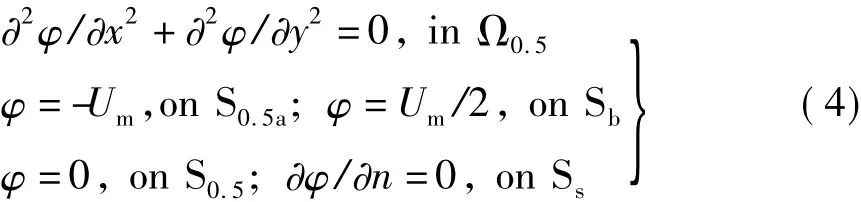
图3(c)给出了通过半场域计算后获得的全场域的电位分布图。显然，图3(b)半场域的静电场边值问题的计算代价要比图3(c)全场域的计算代价低得多。

［讨论3］:对于任意时刻t，即任意相位ωt时，全场域的电位分布关于虚线Ss既非奇对称分布也非偶对称分布。不妨继续向学生提问，能否仍然利用场域Ω结构上的对称性来降低静电场边值问题的计算代价?答案是肯定的，即利用叠加定理将全场域的电位函数分解为关于虚线Ss奇对称分布场和偶对称分布场的叠加。分解过程为如下三步。

(1)将图1电位函数分解为图4(a)和图4(b)所示关于虚线Ss奇对称分布场和偶对称分布场，且A、B和C三相导体的电位分别满足

由上式，得

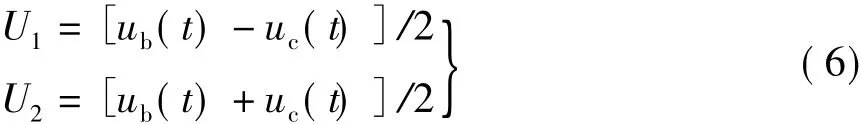
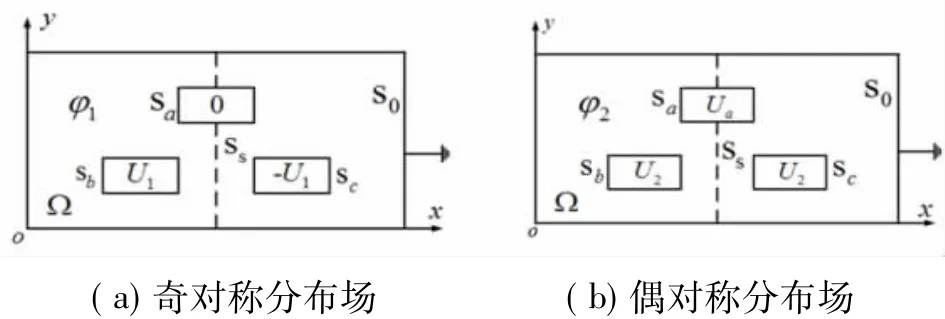
图4 全场域电位分布的分解

(2)基于［讨论1］和［讨论2］，图4(a)和图4(b)可以分别归结为图5(a)和图5(b)对应半场域的静电场边值问题，求解电位函数φ1和φ2的边值问题分别为

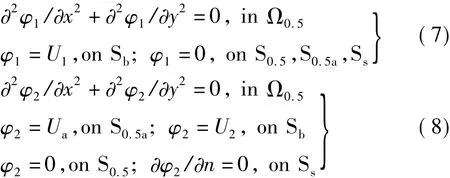
(3)为了求解式(7)和式(8)，由叠加定理得到图1左、右半场域的电位分布分别为

图5(c)给出了ωt=π/3时，通过求解上述两个半场域静电场边值问题获得的图1全场域的电位分布图。

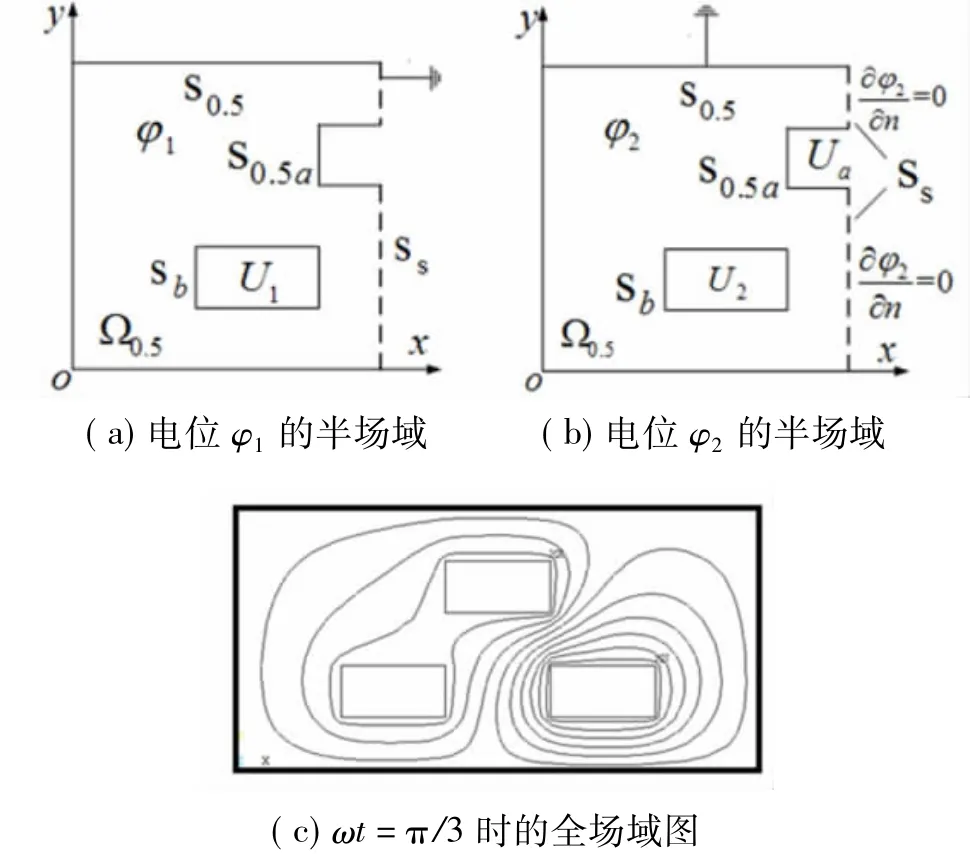
图5 半场域的电位分布

3 电位悬浮导体问题

通过讨论上述三个问题，学生对静电场边值问题的数学抽象及其正确描述有了较深入的理解。为了进一步巩固和加深学生的理解，不妨继续讨论电位悬浮导体问题，如当图1导体Sa电位悬浮且其上单位长总电荷为Q0时的静电场边值问题。如图6所示，导体Sa上的电位不再是已知值而是未知值，设为φa。此时，静电场边值问题可以写为［3］

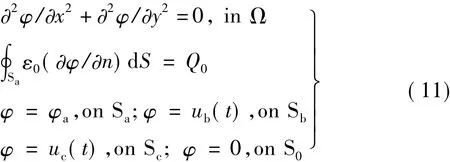
式中，在导体Sa边界积分式中电位函数的法向偏导数为场域外法线方向。

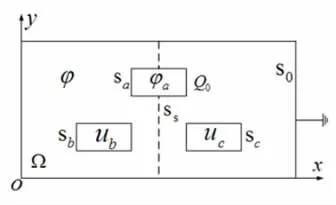
图6 含电位悬浮导体的场域

基于有限元方法，既可以采用电荷守恒法或最小能量法等直接方法求解式(11)，也可以采用虚拟介质法(仅适用于Q0=0的情况)或部分电容法等间接方法求解式(11)［3］。然而，对于一般商业电磁场仿真软件包而言，通常不具备直接求解式(11)的功能。因此，需要与学生讨论的问题是，如何应用商业电磁场仿真软件包求解式(11)?下面，对虚拟介质法和部分电容法进行讨论。

［讨论4］:虚拟介质法仅适用于电位悬浮导体上的总电荷Q0=0的情况。具体方法是:先用相对介电常数远远高于1(如εr≥1000)的虚拟电介质替代图6中的电位悬浮导体Sa，如图7所示的阴影区域Ωa;再求解静电场边值问题。

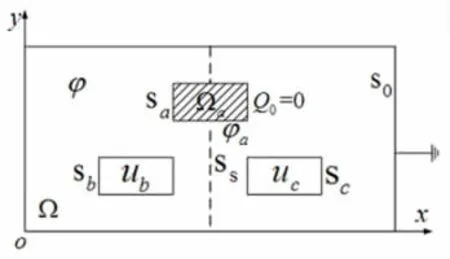
图7 虚拟介质法的示意图

在替代电位悬浮导体的虚拟电介质中，由电介质的极化性质可知:①其内部任意一点的极化电荷密度为零，虽然其边界上存在不同极性的极化面电荷但总量为零，所以虚拟电介质上的总电荷为0;②其内部任意一点的电位移矢量为有限矢量，由于虚拟电介质的相对介电常数远远高于1，导致其内部任意一点的电场强度趋于零，使其内部任意两点的电位差也趋于零，所以虚拟电介质可以近似为电位等位体;③由其边界上电场线的折射定律可知，空气侧的电场线几乎垂直于虚拟电介质表面，其表面近似为电位等位面。上述三点表明，虚拟电介质与总电荷为0的电位悬浮导体的性质相似，因此，式(11)可以改写为

式中，φ+和φ－分别是虚拟电介质边界Sa外侧和内侧的电位函数。应用商业电磁场仿真软件包求解式(12)，虚拟电介质内的节点电位可以作为电位悬浮导体Sa的电位φa。

需要向学生说明的是，相对介电常数εr远远高于1(如εr≥1000)的电介质在实际中是不存在的。虚拟介质法只是数学意义上的等效方法而非物理意义上的等效方法，这也是该方法名称中“虚拟”一词的内在含义。

［讨论5］:部分电容法既适用于总电荷Q0=0也适用于Q0≠0的电位悬浮导体情况。具体方法是:先利用电磁场仿真软件包计算多导体系统的部分电容，并建立等效电路;再由等效电路计算总电荷为Q0时电位悬浮导体的电位φa，将电位悬浮导体转换为电位给定导体的静电场边值问题;最后再次利用电磁场仿真软件包计算电位给定导体的静电场边值问题。

图8(a)和图8(b)分别给出了图6所示多导体系统的部分电容及其等效电路。利用电磁场仿真软件包计算导体系统的部分电容 C10、C20、C11和 C22。由图8(b)等效电路，得电位悬浮导体Sa(节点a)的总电荷为

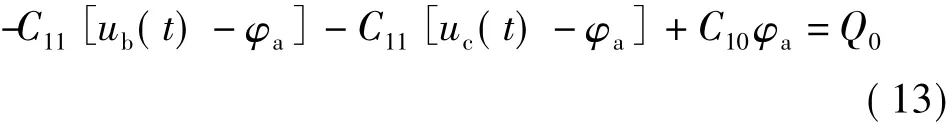
求解上式，得电位悬浮导体Sa的电位为

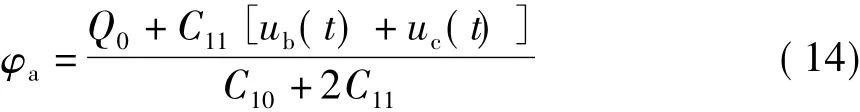
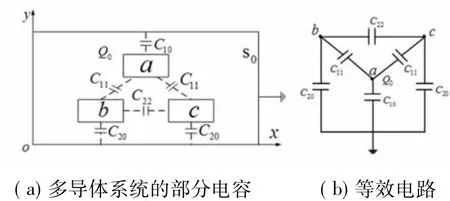
图8 多导体系统的部分电容及其等效电路

至此，图6对应的静电场边值问题式(11)可以改写为

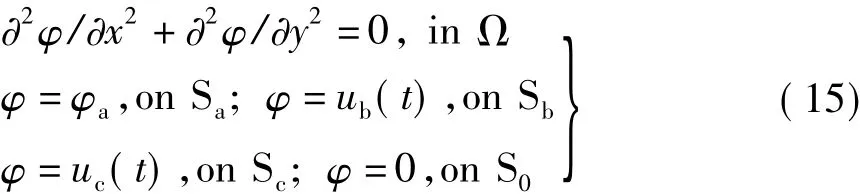
综合上述讨论可以看出，虚拟介质法简单易行且只需要一次电场计算，但不适用于Q0≠0的电位悬浮导体情况;部分电容法虽然有更好的适用性，但需要对多导体系统部分电容的额外计算，计算代价相对较高。

讨论至此，我们不妨再次向学生提问，能否利用图6所示场域结构上的对称性来降低式(11)的计算代价?并继续展开课堂讨论。

［讨论6］:类似［讨论3］仍可以使用叠加定理，将图6全场域的电位分布分解为图4(a)奇对称分布场和图4(b)偶对称分布场的叠加。

对于图4(a)奇对称分布场，需要提醒学生的是，由于导体Sa的电位为0，虽然其上可能存在感应电荷，但由于电场关于虚线Ss呈奇对称分布，导体Sa虚线左侧与右侧的感应电荷大小相等、极性相反，使导体Sa上总的感应电荷为0。因此，无论图6电位悬浮导体Sa是否带电荷，其半场域的静电场边值问题与式(7)相同，不再赘述。

对于图4(b)偶对称分布场，即图9(a)所示电位悬浮导体Sa的情况，可以简化为图9(b)进行分析，其半场域的静电场边值问题为

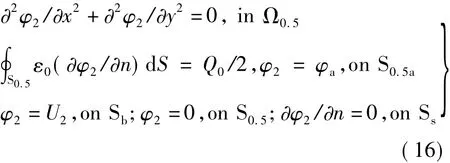
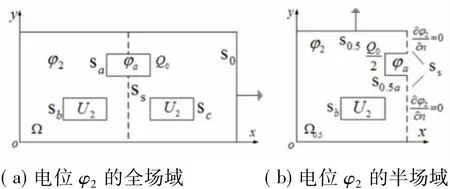
图9 关于虚线Ss偶对称分布的场域

当电位悬浮导体Sa上总电荷为0(Q0=0)时，重画图9(b)为图10(a)。可以采用虚拟介质法求解，如图10(b)所示，其静电场边值问题为

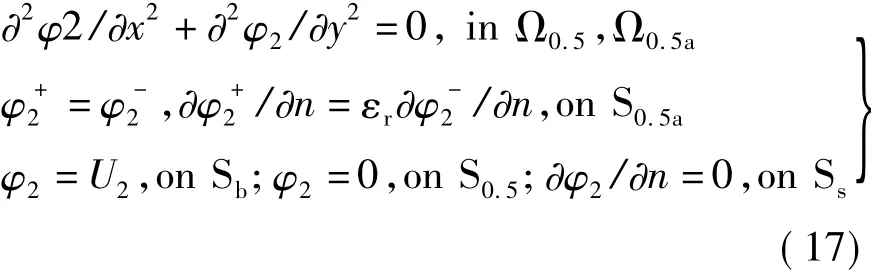
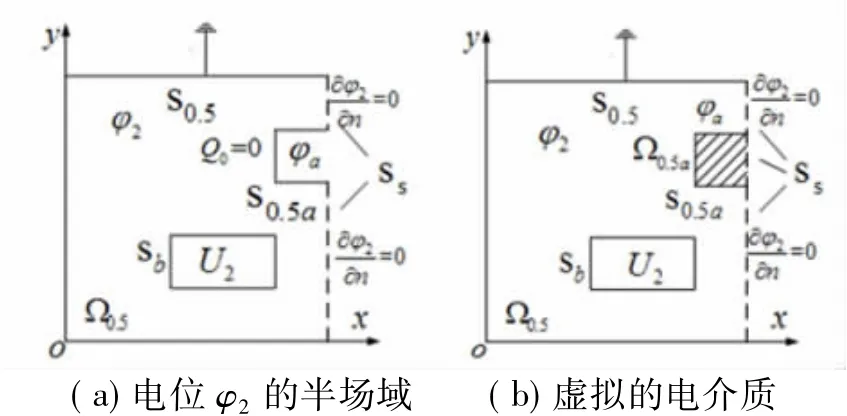
图10 虚拟介质法示意图

当电位悬浮导体Sa上总电荷为任意值时，可采用部分电容法求解。由图8(b)等效电路，图9(b)的等效电路如图11所示。电位悬浮导体Sa(节点a)的电荷为

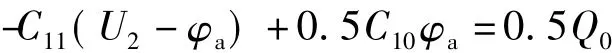
求解上式，得图9(b)悬浮导体Sa的电位为

因此，图9(b)的静电场边值问题便转换为图12所示的静电场边值问题，即

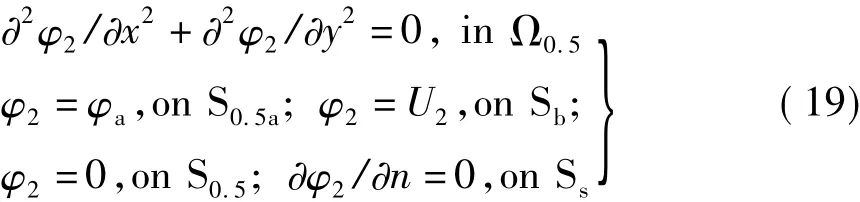
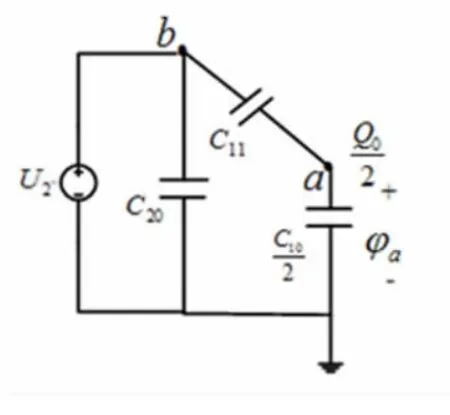
图11 等效电路

图12 电位φa已知

最后，可以由式(9)和式(10)分别获得电位悬浮导体情况下，图6左半场域和右半场域的电位分布图。

4 结语

对工程电磁场问题进行数学抽象并建立其边值问题，是应用电磁场仿真软件包解决工程电磁场问题的前提。在电磁场课程教学过程中，培养学生对工程电磁场问题的数学抽象及其边值问题的正确描述能力，已经成为很多任课教师的共识。本文提供的基于三相电力汇流排的静电场边值问题的教学案例，可以全面地描述三类不同边界条件的静电场边值问题。通过对电位悬浮导体问题的讨论，还可以扩展介质极化、多导体部分电容等概念的应用。

［1］ 教育部高等学校电子电气基础课程教学指导分委员会，“电子电气基础课程教学基本要求”［M］，北京，高等教育出版社，2011年4月

［2］ K.J.Binns，P.J.Lawrenson，Analysis and Computation of E-lectric and Magnetic Field Problems，Oxford，Pergamon Press，1973

［3］ 崔翔，应用有限元方法计算含有电位悬浮导体的电场分布，［M］.保定，“华北电力学院学报”，Vol.22，No.2，1995