变压器等效电路获取的教学方法
2013-08-23谢宝昌
谢宝昌
(上海交通大学电子信息与电气工程学院,上海 200240)
变压器是“电机学”的重要内容之一。对变压器等效电路获取方法的认识有助于正确理解变压器基本原理,也有助于交流感应电机的教学。传统的获取方法是基于变压器内部电磁关系和绕组折算原理获得 T 型等效电路[1,2],学生往往不能理解绕组折算思想而使教学效果大打折扣。
本文提出了一种新的获取等效电路的教学方法,先通过物理过程分析获取电路和磁路耦合模型,然后通过深入分析漏磁路和主磁路中磁通、磁势和磁导关系并引入主磁路铁耗电流分量和磁化电流分量,逐步用电路元件等效替代漏电势源和激磁电流源,而完全电磁耦合部分则用理想变压器替代,最后利用理想变压器的变换特性获得T型等效电路。
1 变压器的物理模型
本文以双绕组变压器为例阐述其等效电路获取的教学过程,该过程也适用于其它类型变压器。
为了让学生理解等效电路获取过程,首先必须解释清楚物理模型,包括参考方向的确定和内部电磁耦合过程。双绕组变压器的参考方向是这样确定的:按照电动机惯例规定端口电压与电流,即电能输入变压器,内部绕组电流与磁场满足右手螺旋关系,磁场与感应电势也满足右手螺旋关系,根据一次侧和二次侧绕组绕向,所有物理量的正方向如图1所示。图中一次侧与二次侧漏磁通仅是与自身绕组匝链的等效漏磁通,即绕组自身漏磁链与匝数之比。
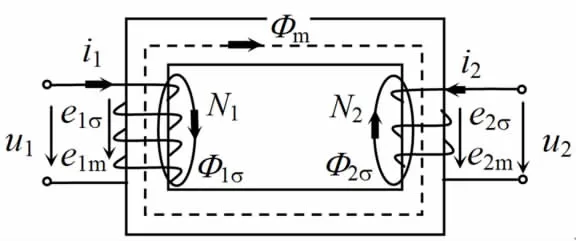
图1 双绕组变压器物理模型
我们在解释内部电磁过程中,必须强调变压器工作频率下电路参数应采用集中参数而不考虑高频或类似雷电波过程的分布参数,这样绕组电阻和电感定义和分离成为可能。同时我们必须强调变压器内部漏磁路和主磁路分开的分析方法即将线性与非线性部分分开。对于漏磁路磁通必须强调是绕组自身全匝链的等效漏磁通。
2 变压器的物理过程
变压器一次侧施加交流电压u1后,变压器内部各物理量都是随时间交变的函数,首先产生一次侧绕组电流i1、主磁场磁通Φm和漏磁场磁通Φ1σ。主磁通Φm不仅与一次侧绕组而且与二次侧绕组耦合并分别感应出主电势e1m和e2m,两者之比等于绕组匝比N1:N2,即变压器变比k。漏磁通Φ1σ只与一次侧绕组耦合并感应出漏电势e1σ。
如果二次侧绕组开路,那么二次侧电流为零,二次侧主电势e2m与端电压u2相平衡。一旦二次侧绕组形成闭合回路,那么二次侧将出现负载电流i2,其产生的磁场将阻碍主磁通Φm的变化,进而一次侧绕组电流i1增大,以维持一次侧交流电压平衡所需的感应电势。与此同时,二次侧负载电流i2将产生与自身耦合的漏磁场磁通Φ2σ并感应出漏电势e2σ。
漏磁通路径主要沿铁芯外的空气隙或油路闭合。磁路线性,漏磁场与绕组电流呈正比,因此可以用漏电感等效绕组相应的漏磁链。
主磁场沿铁芯闭合,将引起铁芯磁滞现象和产生涡流,两者都对主磁通产生影响,即铁芯内的主磁通不仅受一次侧绕组磁势F1=N1i1和二次侧绕组磁势F2=N2i2的影响,还受铁芯磁滞与涡流引起的磁势Fc的影响。
3 变压器的数学模型
我们根据物理模型,可以获得一次侧绕组和二次侧绕组的电压方程与主磁路磁势Fi和F2平衡方程:
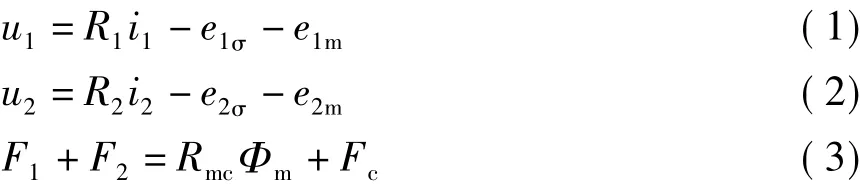
这里,绕组电流i通过绕组电阻会产生压降R1i1和R2i2。
由此获得变压器一次侧和二次侧绕组等效电磁耦合模型,如图2所示。图2(a)和图2(b)分别为一次侧和二次侧电压方程(1)和(2)对应的电路模型。图2(c)是方程(3)对应的简化磁路模型。其中主磁路铁芯磁阻Rmc,一次侧和二次侧绕组漏磁路磁阻分别为Rm1σ和Rm2σ。图中电源正负号表示相应正方向。
因为电流与磁势耦合,磁通与电势耦合,所以图2称为电磁耦合模型。
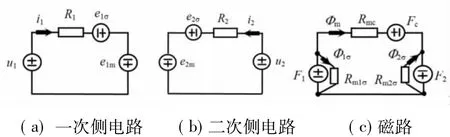
图2双绕组变压器等效电磁耦合模型
由一次侧漏磁路得到漏磁通Φ1σ、漏磁链ψ1σ与电流i1的关系为
Φ1σ=F1/Rm1σ= Λ1σN1i1,ψ1σ= Λ1σN12i1=L1σi1式中,Λ1σ为一次侧漏磁导。
同样地,得到二次侧漏磁通 Φ2σ、漏磁链 ψ2σ与电流i2的关系为
Φ2σ= Λ2σN2i2,ψ2σ=L2σi2
式中,Λ2σ为二次侧漏磁导。
由此可见,漏磁路磁场产生的漏电势在电磁耦合模型中可以用与绕组电阻串联的漏电感表示。
对于主磁路磁势,引入产生磁滞与涡流的等效电流iFe,称其为铁耗电流分量,使得Fc=N1iFe。同时引入产生主磁通的等效磁化电流iμ,使得主磁路磁通磁位降等于N1iμ。于是,由磁势平衡得到各电流之间的关系

其中,激磁电流im等于等效磁化电流与铁耗电流分量之和,它本质上是一次侧和二次侧绕组合成磁势产生的主磁路磁势在一次侧绕组上的电流分量:

一次侧绕组电流i1与负载电流i2相关部分称为负载电流分量,用i1L表示,它们满足关系:

一次侧与二次侧绕组主电势e1m和e2m满足

一次侧与二次侧绕组主电势和负载电流之间关系,即方程(6)和(7)相当于理想变压器模型,于是得到基于理想变压器的等效电路,如图3所示。其中方程(4)的激磁电流im用电流源表示。

图3 基于理想变压器和电流源的等效电路
与漏磁路分析相仿,主磁路磁化电流iμ、主磁通Φm和主磁路磁阻Rmc关系可以表示为等效磁化电感的形式:
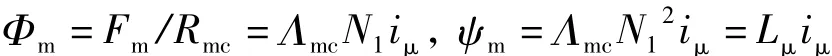
值得注意的是如果主磁路非线性,磁化电感也是非线性的,但变压器正常运行时可以近似认为不变。磁化电流的变化正好满足
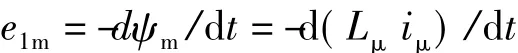
由此说明,磁化电流支路可以用磁化电感与一次侧主电势e1m并联表示。
维持变压器铁芯损耗不变,用等效铁耗电阻表示铁耗电流分量。则铁耗电流分量为
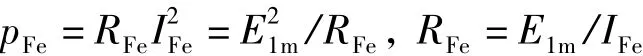
式中,RFe为等效铁耗电阻,IFe为等效铁耗电流有效值,E1m为一次侧绕组主磁场感应电功势有效值。
由此获得铁耗电流支路可以用铁耗电阻与一次侧主电势并联表示。
图3和方程(5)的激磁电流源用铁耗电流与磁化电流分量表示,正好用铁耗电阻和磁化电感并联的无源电路元件替代,得到图4所示的等效电路。
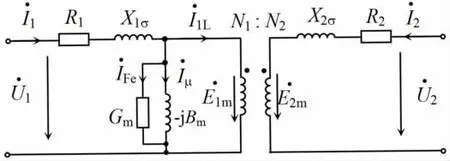
图4 基于理想变压器的等效电路
如果图4中所有电量都是以同一角频率ω正弦规律变化的,那么可以表示成相量的形式。其中电感用电抗表示:X1σ= ωL1σ,X2σ= ωL2σ;激磁支路的并联铁耗电阻和磁化电感分别用激磁电导Gm=1/RFe,激磁电纳Bm=1/ωLμ来表示。基于理想变压器的相量等效电路如图5所示。
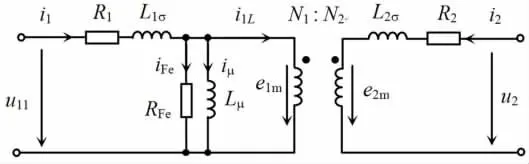
图5 基于理想变压器的相量等效电路
最后,将图4中的理想变压器消除,可以得到折算到一次侧或二次侧的T型等效电路。利用理想变压器的阻抗变换特性,将二次侧漏阻抗Z2=R2+jX2乘以变比平方折算到一次侧=+=k2Z2,将二次侧电压乘以变比折算到一次侧u'2=ku2,二次侧电流除以变比折算到一次侧=i2/k(其数值等于一次侧电流的负载分量但方向相反),变换后的等效电路如图6所示。
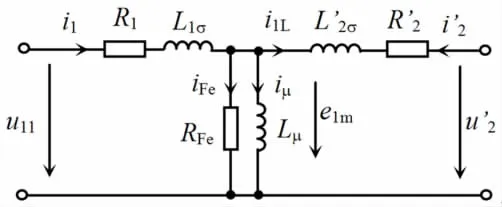
图6 变压器的T型等效电路
4 结语
本文提出的基于电磁耦合模型推导等效电路的教学方法避免了直接用电磁场方法带来教学上的困难,针对教学课时数紧张的现状,能起到事半功倍的教学效果。本文讲解绕组折算可以让学生直观地比较电磁场方法与电路和磁路相结合方法,其结果是一致的。这种教学也适合“电机学”课程中其它类型变压器的教学过程。
[1] 许实章,电机学[M],北京,机械工业出版社,1982年
[2] 周顺荣,电机学[M],北京,科学出版社,2007年
