基于宏程序的椭球面加工刀路算法

胡翔云，肖仁

(湖北职业技术学院，湖北孝感432000)

某厂电加工用的铜电极外形为椭圆柱上接一半椭球面 (如图1所示，其在xOy、xOz、yOz平面及平行于它们的平面上的截痕均为椭圆)，其中的半椭球面需要在数控机床上加工。该加工特征可以采用计算机自动编程，但当尺寸发生变化时，需要修改程序，不能满足不断变化的生产实际需要［1］。为此，工厂试图编制宏程序来实现加工。零件外形为规则的空间曲面，适宜于采用层切法加工［2］，根据加工用途的不同，可选用立铣刀、球刀、牛鼻刀等刀具切削。这里通过建立3种刀具加工椭球面的数学模型，求出刀心轨迹方程，并基于FANUC数控系统编制宏程序，方便工厂生产该类零件。

1 求刀心轨迹参数方程

为分析方便，这里先以球刀加工椭球面为例建立数学模型，然后给出立铣刀、牛鼻刀切削时刀心轨迹数学模型 (实际生产中，先用立铣刀开粗，然后用球刀或牛鼻刀进行半精加工和精加工)。

图1 使用球刀加工椭球表面

如图1所示为球刀加工椭球面的三视图，工件坐标系原点建立在半椭球的球心。设椭球在xOz平面上的椭圆截痕长半轴、短半轴分别为a、b，在yOz平面上的椭圆截痕长半轴、短半轴分别为c、b，则在xOy平面上的椭圆截痕长半轴、短半轴分别为a、c。刀头半径为r。

设球刀刀头在点M(其在俯视图、左视图中对应位置为M1、M2)处与椭球面相切，用一过点M的水平面截取椭球，它们的交线为虚线椭圆O2;用一过点M、且与yOz平面平行的平面截取椭球，则它们的交线为虚线椭圆O3。点M的z坐标为i，O3M2与水平面的夹角为θ(0°≤θ≤90°)，O2M1与x轴的夹角为 β (椭球转角)(0°≤β≤360°)。

为求刀心O的坐标xO、yO，先需求出虚线椭圆O2的长半轴e和短半轴f。

为求e之值，以主视图中椭圆为研究对象，解方程:

为求f之值，以左视图中椭圆为研究对象，解方程:

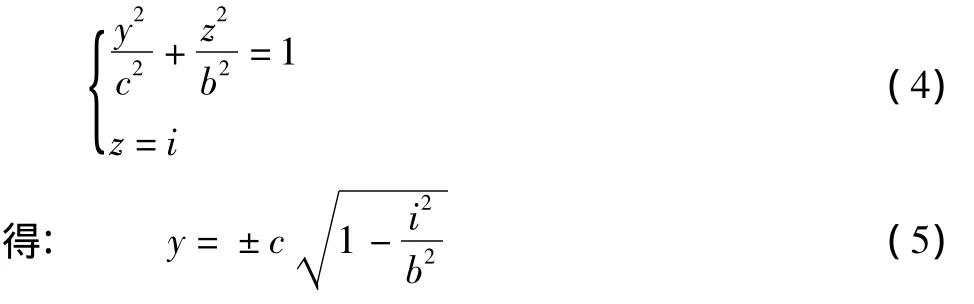
根据三视图中俯视图与左视图“宽相等”的原理［3］，得虚线椭圆O2的短半轴为:

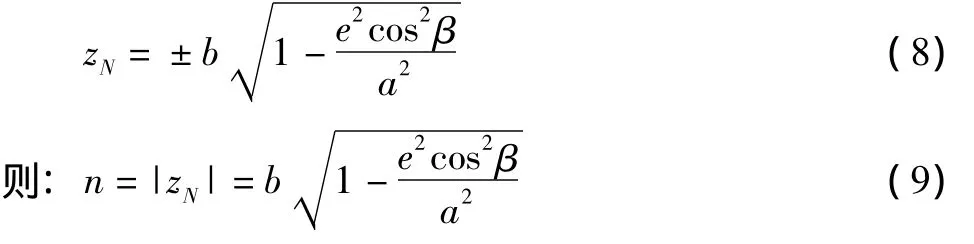
同样的方法可以求得:

在俯视图中，过点M1作虚线椭圆的切线ll'，设其斜率为kl，OM1的斜率设为kOM1。对虚线椭圆O2的方程求导，得:

代入xM1、yM1之值，则有:

因为OM1⊥ll'，故:

从而有:

所以有:

用类似的方法可求得刀心O的z坐标:

从而得到刀心O的运动轨迹参数方程:

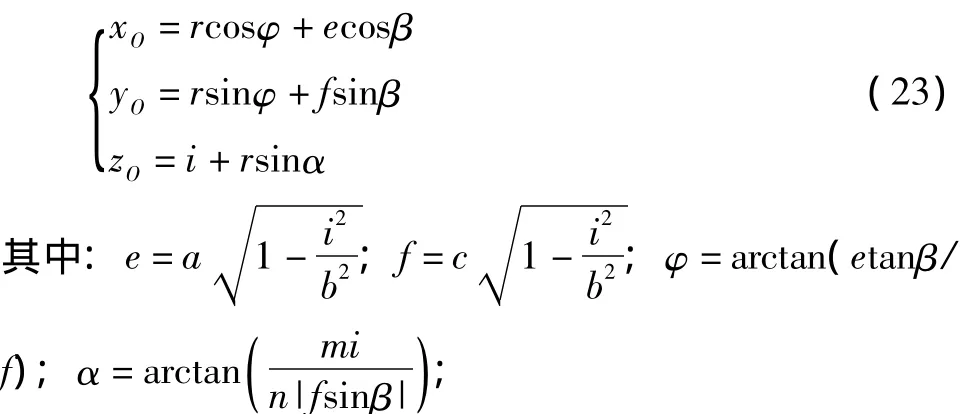
r为球刀半径;

i、β分别为高度变量和椭圆转角变量;

xO、yO、zO为刀心O的坐标。

由参数方程 (23)可知，采用球刀层切法加工椭球面时的刀心轨迹是空间曲线。使用球刀切削时，刀头始终与椭球面相切，因而加工精度高，但加工效率低，适用于半精加工及精加工。

数学模型中有两个变量，所以，需要采用两个嵌套的循环语句实现编程［5］。由于圆可认为是长轴与短轴相等的椭圆，故该模型同样适用于半球零件的加工。

当采用立铣刀切削椭球面时 (如图2所示)，刀心轨迹方程变为:

其中:e、f、φ、r、i、β的含义与式 (23)相同。

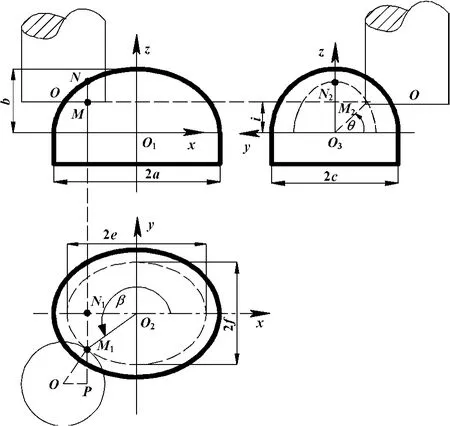
图2 使用立铣刀切削椭球面

使用立铣刀切削，切削效率高，但切痕残留高度大，适宜于椭球面的粗加工。

当采用牛鼻刀切削椭球面时，由于牛鼻刀有刀具半径R及刀刃圆角半径r两个参数 (如图3所示)，其刀心也在底部中心，其刀心轨迹O的方程为:

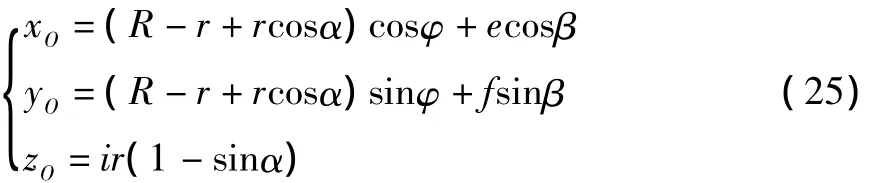
图3 使用牛鼻刀切削椭球面

在加工椭球面时，牛鼻刀刀面始终于椭球面相切，因而有与球刀一样的加工精度，且其强度和刚度比球刀更好，适用于椭球面的半精加工和精加工。

从参数方程 (23)、(24)、(25)可知:立铣刀、球刀、牛鼻刀加工椭球面时刀心轨迹坐标是高度变量i和水平面内的椭圆转角变量β的函数 (α、θ、φ、e、f中间变量均为i、β的函数)，因而可利用两个条件循环语句编制零件宏程序［4］。

2 编写宏

这里基于FUNAC Series 0i-Mate-MODEL D数控系统，以球刀加工椭球面为例编制宏。工件坐标系原点建立在椭球的对称中心 (如图1所示)。程序中各变量含义如表1所示。

表1 宏程序中各变量的定义

程序如下:

O9018

#PI=#3101;//用PI表示圆周率π

#11=0;//给高度变量i赋初值

WHILE［#11LE#2］DO1;//#2为椭球短半轴b

G00X［#1+#18］Y;#2+#18］;//球刀定位，#18为球刀刀头半径(由加工程序指定)，#1为椭球长半轴a

G01Z#6F50;//下刀

#4=#1*SQRT［1-#11*#11/;#2*#2］］;//计算e值

#5=#3*SQRT;1-#11*#11/;#2*#2］］;//计算f值

#10=0;//给转角变量β赋初值

WHILE;#10LE;2*PI］］DO2

#8=ATAN;#4*TAN［#10］/#5］;//计算 φ 之值

#6=#3*SQRT;1-#4*#4*COS;##10］*COS［##10］/;#2*#2］］

#7=#2*SQRT;1-#4*#4*COS;##10］*COS;##10］/;#1*#1］］

#9=ATAN;#6*#11/;#7*ABS［SIN;#10］］］］;//计算 α 之值

#14=#11+#18*SIN;#9］;//计算 zO，

#12=#18*COS;#8］+#4*COS;#10］;//计算 xO

#13=#18*SIN;#8］+#5*SIN;#10］;//计算 yO

G01X#12Y#13Z#14F120;//进行直线插补，使球刀切削点逼近椭圆弧

X#4Y0;//直线插补至高为i处椭圆的长轴处

#10=#10+PI/72;//确定转角步距，步距角为π/72(弧度)

END2;//结束转角循环

#11=#11+0．5;//提刀步距确定为 0．5 mm

END1;//结束提刀循环

G00Z10;

M99;

使用立铣刀、牛鼻刀切削时的编程方法与此相似，这里不再赘述。

3 应用实例

半椭球铜电极长半轴为100 mm，短半轴为60 mm，椭球宽40 mm。现对其进行精加工，使用球刀，刀头半径为8 mm。使用第一类自变量指定法［5］，则加工程序如下:

O1234

G54G00X0Y0Z50

M03S1500

G65P9018A100．0B60．0C40．0R8．0;//调 用 宏9018，并通过A、B、R对#1、#2、#18传递数据

G00Z50;

X0Y0;

M05;

M02;

由此可见，有了上面的宏程序，则编制椭球类、球类零件加工程序就非常容易 (只需用G65指令调用宏O9018，并给椭球长半轴、短半轴、椭球宽、球刀半径赋值就行了)，相当于给数控系统增加了一个固定循环指令。

4 结束语

通过层切法加工椭球面的工艺分析，分别建立了球刀、立铣刀、牛鼻刀切削椭球面时的刀心轨迹参数方程，并以此为依据，以球刀精加工为例，用两个嵌套的循环语句编写宏程序，实现该类零件程序的参数化。当零件尺寸变化时，只需给宏程序中有关变量赋值就能完成零件加工，大大缩短了编程时间。实际生产中，可用立铣刀开粗、用球刀或牛鼻刀半精加工和精加工，以提高加工效率和加工质量。

【1】王秋红，葛胜兰，陈德华．利用FANUC宏程序铣削半球零件的3种方法［J］．机床与液压，2011，39(16):81-84．

【2】赵晓燕，刘志刚．宏变量在数控加工中的应用［J］．现代制造工程，2010(8):121-122．

【3】赵大兴．现代工程图学［M］．武汉:湖北科学出版社，2008:68-69．

【4】王锋波，孙士彬．FANUC系统宏程序在抛物线类零件中的应用［J］．煤矿机械，2011(10):148-150．

【5】BEIJING-FANUC．FUNAC Series 0i-Mate-MODEL D 加工中心系统用手册．B-64304CM/01［M］，2010:263-266．