强烈地震作用下结构塑性位移刚塑性计算方法

杨永兴

(山西煤炭运销集团运城有限公司，山西运城 044000)

0 引言

结构的性能以及其在地震作用下的损伤程度与结构的位移有着直接的联系，当施加荷载使结构的某些部位产生塑性变形，经过多次重复后导致结构的塑性积累损伤破坏。结构在强烈地震的作用下进入塑性阶段，必须具备承受较大的塑性位移的能力，通过塑性变形来消耗地震的能量，以符合“大震不倒”的要求。因此，结构在强烈地震作用下的塑性分析十分必要。然而，结构的塑性分析是一个极其复杂的非线性过程。通常，结构被假定为弹塑性模型。本文研究表明地震越强烈，在结构总的位移中塑性位移所占的比例越大，弹性位移可以忽略，可以用刚塑性模型计算结构的位移。

1 弹塑性与刚塑性响应的比较

刚塑性模型常用来描述在静载作用下产生较大塑性变形的结构性能。通常认为利用刚塑性模型进行结构动力分析会不能研究共振。然而，本文研究表明微小的塑性变形也会破坏共振。对于单自由度体系，受到简谐动力荷载F sinθt的激励，若阻尼比ξ=0.05，F/Fy约为0.1时，如图1所示结构进入塑性阶段，位移幅值急剧下降，在强烈地震作用下结构不会产生共振现象，随着简谐力幅值与屈服力的比值增加，弹塑性计算的位移幅值趋近于刚塑性计算的幅值，因此在强烈地震作用下可以采用刚塑性模型来计算结构的塑性位移。

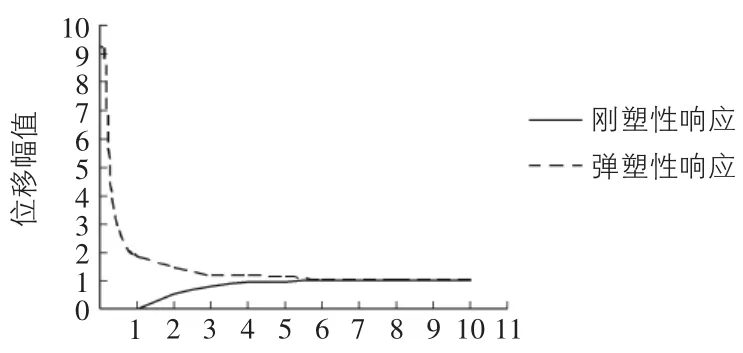
图1 刚塑性与弹塑性在谐激励下位移幅值

1.1 弹塑性运动方程

对于单自由度体系，当满足式(1)或式(2)体系处于弹性阶段，运动方程为式(3):

式中:x——相对地面的总位移，x=xe+xp;

xe——结构的相对弹性位移;

xp——结构的相对塑性位移;

ξ——结构的阻尼比;

Fy——结构的屈服极限。

式(3)与式(5)是按照理想弹塑性模型建立的运动方程，在弹性阶段能量主要靠粘滞阻尼来耗散，在塑性阶段主要靠塑性变形来耗散能量。

刚塑性模型建立的运动方程:

检查施工表面的干燥状况，均匀洒水进行保湿，待面层全部处理完成后采用专用喷涂机对表面进行均匀细致的喷涂一遍清洗剂，杜绝漏喷、多喷、堆积等现象；喷涂完成后表面用薄膜紧密的覆盖一层，用砖块、木方等重量物体压盖严实薄膜周边。

1.2 两种模型计算单自由度体系塑性位移差别分析

结构进入塑性阶段，弹塑性模型的振动方程和刚塑性模型的振动方程形式上是相同的，但是算得的最大塑性位移是有差别的。产生差别的原因主要是二者进入塑性阶段的初始条件不同，刚塑性模型的塑性运动总是从静止开始，而弹塑性模型的塑性运动总是从运动开始的，具有一定的初动能。二者的差别如式(9)所示。

其中，ξ为结构的阻尼比;ωd为结构的自振频率;ω为结构无阻尼自振频率;T为结构周期;Δt为荷载作用持续时间;x1为体系最大的负位移。

由式(11)可得:

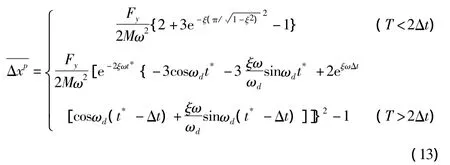
当阻尼比 ξ=0.05，当 Δt=0.12 s，式(12)为两种模型计算位移差别上限的最小值。当体系振动周期T≤0.6 s时，ξ=0.05时，式(12)可以近似写成式(14):

2 弹塑性模型与刚塑性模型响应

为了研究在地震作用下，利用刚塑性模型计算塑性位移的误差。结构的阻尼比为0.05，首先保持Fy/Mg=0.2不变，式中的Mg为结构的重力荷载代表值按规定计算。在地震的作用下，计算了在不同自振周期时，两种模型计算塑性位移差别情况(见表1)，结果如图2所示。不考虑结构的阻尼，当Fy/Mg固定，对地震的加速度按比例增大对结构的响应进行计算，所得结果如图3所示。

表1 选择的地震波

图2 表1地震作用下Δxp值的变化

3 刚塑性位移计算反应谱法

反应谱是单自由度体系对于某个实际地震地面运动的最大响应与体系的自振特性之间的函关系曲线，是描述地震动特性的重要工具，但从式(7)和式(8)可以看出，刚塑性模型的位移响应只与参数Fy/Mg的值有关而与结构其他特性无关，这样在给定的地震作用下，利用非线性时程法计算出体系的最大位移，建立最大位移与Fy/Mg关系曲线即刚塑性反应谱(如图4所示)。由于在计算刚塑性反应谱时所采用的地震波加速度的最大值amax不同，因此必须进行转化，把计算的位移谱的纵轴和横轴同时乘以系数β=1/amax。

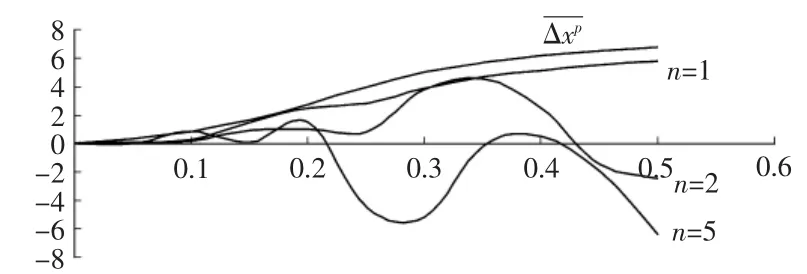
图3 TAFT地震波放大n倍Δxp值变化

图4 刚塑性反应谱

4 算例

某高速公路上的钢筋混凝土高架桥，位于设防烈度为8度设计基本地震加速度为0.3g的地区。上部结构的重力荷载为190 kN/m，由高9 m的圆形柱子支撑，桥的总跨度为39.6 m，柱子的直径为1.5 m，对于横向地震作用的计算可以把高架桥看作单自由度系统(见图5)。经计算可知，柱子的刚度K=9.6×103kN/m，侧向屈服力Fy=839.7 kN，结构的自重荷载为G=Mg=7 517 kN。

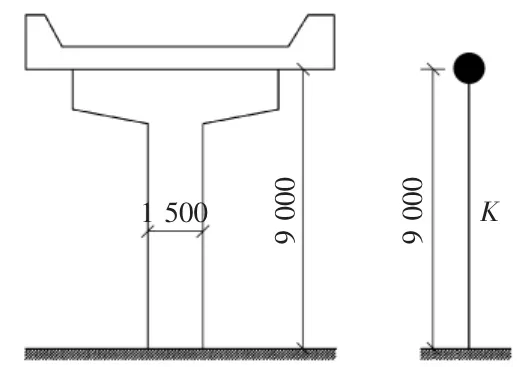
图5 结构断面与模型

由文献［8］可知在强烈地震作用下时程分析时地震加速度的最大值为 0.51g。Fy/Mg=0.11，α =1/0.51=1.96，ay=0.11 ×1.96=0.216，由刚塑性位移谱图4可得，结构的塑性位移为17/1.96=8.67 cm，结构的屈服位移为 Fy/K=839.7/96=8.74 cm，结构的弹塑性位移为17.41 cm。利用ANSYS有限元程序输入TAFT地震波弹塑性时程分析，计算结构的最大塑性位移为9.1 cm，最大弹塑性位移为17.96 cm。

结构利用本文的刚塑性位移谱法计算的结果与有限元弹塑性时程分析的结果最大塑性位移相差4.7%，最大弹塑性位移相差3.1%，在建筑结构分析计算中所允许的。

5 结语

1)在强烈地震作用下，可以用刚塑性模型来计算结构的响应，只要结构有微小的塑性变形就不会产生共振现象。

2)结构的自振周期越短，Fy/Mg值越小，地震加速度峰值越大，结构的位移响应越接近刚塑性响应。

3)结构的自振周期不超过0.6 s时，利用刚塑性模型与弹塑性模型计算的最大塑性位移差别不会超过式(14)计算结果，在实际工程中可以忽略由式(14)计算出的误差。

4)刚塑性模型计算结构的弹塑性位移与塑性位移过程简单，容易掌握，利用本文提出的刚塑性位移谱法计算结构在强烈地震作用下的最大塑性位移比弹塑性时程法计算结果偏小，但误差在10%以内，符合建筑结构计算设计要求。

［1］ A.Paglietti，M.C.Porcu.Rgid-plastic approximation to predict plastic motion under strong earthquakes.Earthquake Engineering and Structural Dynamics，2001(30):115-126.

［2］ Anil K.Chopra.结构动力学理论及其在地震工程中的应用［M］.谢礼立，吕大刚，译.北京:高等教育出版社，2007.

［3］ Lai SP，Biggs JM.Inelastic response for a seismic building design.Journal of Structural Division ASCE，1980(106):1259-1310.

［4］ 爱德华·L·威尔逊.结构静力与动力分析—强调地震工程学的物理方法［M］.北京金土木软件技术有限公司，中国建筑标准设计院，译.北京:中国建筑工业出版社，2006.