基于k/N 保障系统的连续施工设备配置优化分析

刘云 李敏

(1.陕西咸阳古建集团有限公司，陕西咸阳 712000;2.西安铁路职业技术学院，陕西西安 710014)

工程施工过程中设备系统能否正常工作决定了工程任务的完成效果，特别是在抢险过程中，施工设备往往需要连续工作，保障工作设备的正常工作就显得尤为重要，然而在实际工作过程中要求所有的设备同时正常工作难度会很大，准备备用设备就成为必然，一旦发生设备故障则可用备用设备替代，从而保证工作能连续完成。若备用设备数量足够多则工程必然可以顺利实施，但这一结果是以牺牲成本为前提的，其实在实际工作过程中这种情况完全没有必要，我们需要的是整个工作系统的工作状态正常，当组成工作系统的具体设备有个别失灵，只要事件不影响系统工作结果，就完全可以不必考虑，所以备用件的个数越少越好。

以某施工单位进行抢修作业为例，为能够短时间、高效率的完成任务，共安排5套设备同时作业，而实际只要其中3套设备能正常工作，就能保证整个抢修系统工作正常，这时这5套设备就构成了一个工作系统，其中的2套设备构成备用设备，我们将这种系统称为k/N系统。由于k/N系统具有高可靠性，在施工作业中，尤其是在使用一些高科技的设备工作中被越来越多的应用。

k/N系统理解起来很简单，但是最关键的问题是在一定概率要求的条件下，如何确定保障工程系统正常工作的设备的最小备用保有量，即设备保障量的最优值。由于设备工作的具体状况复杂多变，为了更清楚的研究问题，本文将按单阶段任务和多阶段任务两种情况来进行分析。

1 单阶段任务中的k/N系统设备保障量分析

假设某任务的完成方式为单阶段一次完成，所需时间为T，完成任务所需要的设备中的某种构件可以形成k/N系统，其中该构件的失效率为λ。这一系统在执行工作任务的时候，当有构件发生故障后，需要依据“备用设备消耗量最小”的原则，即只要不影响设备完成当前任务，就不需要进行故障部件的更换，此时只要工作部件的数量能够不小于k，那么就可以保证整个系统正常工作。但是当发生故障的部件过多，从而导致系统中能够正常工作的部件数量小于k时，整个系统就无法顺利工作了，此时则需要立刻更换设备，以便系统可以继续正常工作。

建立数学模型，要求备用设备的保障率不小于已经给定的概率P，从而求解出在单阶段任务状态下设备保障量的最优值S。

我们可以把这种情况下k/N的系统按照其在任务执行期间发生的失效过程分为两个不同的阶段:发生故障后对故障件进行修理的阶段和无法修理需要更换故障件的阶段，这两个阶段的变化过程如图1所示。

设t为两个阶段的分割时间点，在t时刻以前，系统中部件故障不更换，在t时刻以后，部件故障立刻用备用设备替换。也就是说，在0～t期间，系统中共有N－k－1个部件发生故障，在t～T期间，每有一个部件发生故障就立即更换，系统一直保持仅有k个部件工作的状态，那么，在t时刻，恰好出现N－k个部件故障。

图1 k/N系统阶段变化过程

设P(N，k，T，j)为在任务期间恰好消耗j个备用设备的概率，s为面向任务的设备储备量。

当j=0时，即任务期间没有更换备用设备，那么整个任务都处在不更换故障件阶段(t＞T)，在任务期间故障件的数量不大于N－k－1。此时:

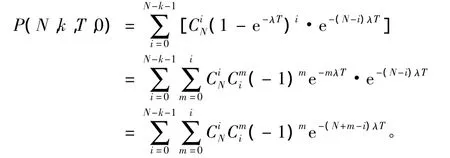
当j＞0时，即任务期间更换了j个备用设备，此整个任务必然包含了不更换故障件阶段和更换故障件阶段，则t≤T，设f(t)为间隔点的概率密度函数，此时:

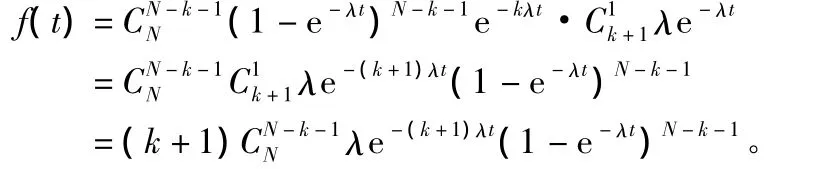
在更换故障件阶段共消耗j个备用设备的概率恰好等于由k个部件组成的串联系统在T－t时间内消耗j个备用设备的概率:

然后再用计算 P(N，k，T，j)。

其中，P(N，k，T，j)即为任务期间正好需要j个备用设备的概率，而P(j≤s)则表示单阶段任务期间备用设备需求量j≤s的概率。那么:

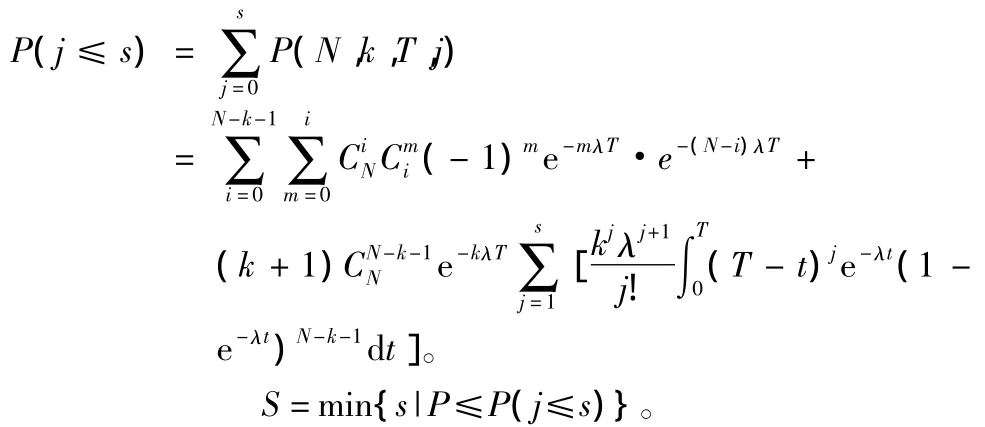
这里S就是所求的最优设备保障量。

2 多阶段任务中的k/N系统设备保障量分析

单阶段任务发生的状况一般比较简单，但大多数情况下任务的发生是由不同的工作阶段共同组成的，各阶段之间互相影响，也就是我们所称的多阶段任务。这种情况下，k/N系统结构中的N和k只会随着任务阶段的变化而变化，各阶段要求的工作部件数量也不同，也就是说这个k/N系统在各个阶段的任务中是不同的。

假设一个多阶段任务可以被分解为L个阶段性任务，其中各构件的配置数为N，各阶段任务的完成时间为Tl。该k/N系统会随着各阶段需完成的任务要求变化，设在第l(l=1，2，…，L)个任务中，起先有kl个可工作部件，任务要求工作期间至少要保证Kl个部件工作，此时系统为Kl中取kl系统。要求备用设备保障率不小于P，多阶段任务期间最优设备保障量为S。

令第l阶段备用设备消耗量为jl，该阶段结束时的可工作部件恰好是下阶段任务开始时的可工作部件数 kl+1，P(kl，Kl，Tl，jl)为任务期间备用设备消耗的概率。

通过分析可知，若kl≥Kl，则kl可取设备基本保障量Kl，每阶段问题可按单阶段情况来处理;若kl＜Kl，则要按照备用设备消耗量最小的原则先对整个系统进行整修，更换Kl－kl个故障件，然后再开始执行该阶段任务，此时系统可被看作是由Kl个部件组成的串联系统，如图2所示。

图2 多阶段任务执行示意图

在kl＜Kl的前提下，当本阶段任务准备的备用设备数jl≥Kl－kl时，系统可以被看作一个由Kl个部件组成的串联系统;然而当本阶段任务备用设备数jl＜Kl－kl时，表示用来替换Kl－kl个故障件的备用设备不够用，任务将无法继续执行。

根据上面的结果分情况讨论可得:

设系统在每个阶段任务开始时的可工作部件数量为k1，k2，…，kL，在该阶段任务结束时可工作部件数量为k*(k*≥KL)，且总备用设备消耗量恰好为 s的概率为 P(k1，k2，…，kL，k*，s)。则:

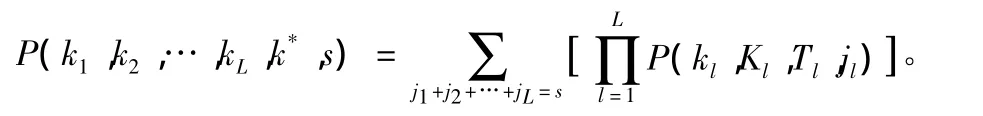
设P(s)为系统在此多阶段任务中恰好消耗s个备用设备的概率，则:

设P(j≤s)则表示多阶段任务期间备用设备需求量j≤s的概率。那么:

那么:

这里S就是所求的最优设备保障量。

3 应用实例

某施工抢修作业设备包含5个同类型的部件，部件的发生失效的概率为λ=0.001 h－1，部件发生失效的情况之间互不干扰。现在该设备要完成一个抢险任务，任务全程可分为3个阶段，在第1阶段，任务的工作时间为100 h，要求至少保证2个部件工作正常;第2阶段的工作时间为250 h，至少要有3个部件工作正常;第3阶段的工作时间为250 h，要求至少保证2个部件工作正常。需要在备用设备保障率不低于 0.90，0.95，0.99 的条件下，确定该部件的最优设备保障量。利用前面建立的数学模型，可以得到结果如表1所示。

表1 最优设备保障量核算结果

由此可知当需要工作顺利完成时，若备用设备的保障率要达到90%，只需提供一个备用设备即可。

［1］张亨佳.工程机械中的常见故障分析及维修［J］.沿海企业与科技，2005(5):32-36.

［2］王 强，黄 诚，高坤华，等.机械设备维修备用资源储备量的确定［J］.改装维修，2003(4):65-71.

［3］鲍敬源，王航宇.装备维修中备用资源需求率的预计方法［J］.海军工程大学学报，2003(4):101-108.

［4］包菊芳.备用资源储备定额研究［J］.物流技术，2002(7):3-7.