氢修饰石墨烯纳米带压电性质的第一性原理研究
2013-08-22刘源姚洁陈驰缪灵江建军
刘源 姚洁 陈驰 缪灵 江建军
(华中科技大学光学与电子信息学院,武汉 430074)
(2012年8月22日收到;2012年11月8日收到修改稿)
1 引言
材料的压电性质应用非常广泛,早在20世纪初,人们就已经开始对压电效应进行研究[1].1894年沃伊特指出,介质具有压电性的条件是其结构不具有对称中心.然而初期对于压电性质的理论研究大部分停留在宏观层面,对于压电性质的微观机理还不是很清楚.1994年,Philippot等[2]在研究石英类晶体性能与结构关系时发现,压电效应与结构内四面体扭转角δ有关.之后,随着计算技术的发展以及Vanderbilt等[3]极化理论的被普遍认可,人们已经可以通过理论计算的方式对材料的压电性能进行微观的分析.其中忻隽等[4]利用第一原理计算和实验表征手段进行研究后发现,压电张量是表征晶体偏离中心对称程度的序参量,偏离中心对称越远,压电张量的模也越大.
随着纳米材料的新兴,各种具有良好压电性能的纳米材料[5-7]也开始被人们广泛研究.2010年,Agrawal等[8]从理论上研究了ZnO纳米线中压电效应与纳米线尺寸之间的关系,并且指出这一尺寸效应的主要机理是纳米线自由表面的电荷重新排布而引起的局部极化.尤为有趣的是,Qi等[9]发现,边缘用氢钝化后BN纳米带同样具有一定的压电特性,其边缘的氢钝化作用使得该结构具有了一定的电偶极矩非平衡排布,同时,BN纳米带本身具有的不对称BN六元环,在拉伸作用下整体结构的正负电荷中心发生定向偏移,甚至使得结构电偶极矩发生偏转,从而使得该结构具有了较好的压电特性.
然而,被广泛研究的石墨烯结构却不具备这一性质,根本原因在于其结构的高度对称性.结构决定性质,C,C六元环的完全等价性,使得形变对其正负电荷中心位置的改变几乎为零.随着对石墨烯研究的深入,人们从最初研究其制备和基本的电子性质方面[10-12],开始转向对石墨烯的改性研究.比较典型的有纳米团簇的掺杂[13,14],SiO2衬底的掺杂[15,16],空位缺陷[17-19]以及原子、分子尺度的掺杂[20-22].而在石墨烯的原子分子尺度掺杂中,由于氢原子的独特性质与氢气的广泛应用,使得石墨烯的氢原子掺杂在石墨烯改性以及储氢等领域都有很广泛的研究[23-25].其中Subrahmanyam等[25]在2011年对石墨烯的储氢研究中发现,石墨烯能够吸附5 wt%的氢原子,并且这些氢原子能稳定地吸附在石墨烯的同一侧.以上结果从实验以及理论上说明,石墨烯上的氢原子掺杂是一种很有效的改性方式.
此前由于石墨烯的结构高度对称性,人们几乎没有进行石墨烯压电性质方面的研究.本文从氢原子掺杂着手,设计了一种氢原子间隔吸附于石墨烯纳米带上的结构,并研究其电极化性质.氢原子的间隔插入不仅导致石墨烯纳米带的初始电极化状态发生有趣的改变,更重要的是,有氢原子修饰和无氢原子修饰的C原子也变得不等价.本文通过第一性原理计算方法,对氢修饰后的石墨烯纳米带进行结构优化以及一定的拉伸作用,从电偶极矩密度的变化规律中探讨其压电性质.最后对石墨烯纳米带其他不同的氢修饰模式进行系统的研究,从电偶极矩密度方面研究其压电性质的可调性.
2 计算模型与方法
本文中讨论了氢修饰情况下不同宽度(1,2,3和4 nm)的锯齿型石墨烯纳米带(zigzag graphene nanoribbons,ZGNRs)结构,ZGNRs表面上的间隔位置吸附了H原子.图1所示为2 nm宽度下的结构模型,以下简称2 nm H-ZGNRs.虚线框内为计算的原胞单元,其中包含16个C原子,6个H原子.为消除相邻ZGNRs之间的相互作用影响,在所有计算的周期性结构中,设置z方向相邻ZGNRs片层间距离大于15˚A,在x方向片层两边保证10˚A以上的真空层.

图1 2 nm H-ZGNRs的原子结构,上图为俯视图,下图为侧视图
本文计算基于第一性原理密度泛函理论方法[26,27]的SIESTA软件包[28].在计算中,选取交换关联泛函为局域密度近似[29]中的CA-PZ[30]近似方法,芯电子采用模守恒赝势描述.基矢展开波函数截断能Ec为150 Ryd.在结构优化时,原子受力的收敛精度为0.05 eV/˚A,电荷密度矩阵的收敛标准为10-4.对于不同宽度的石墨烯纳米带结构模型,K点网格设置为1×8×1.
3 结果与讨论
3.1 H-ZGNRs中的不对称C-C结构
本文首先对氢原子掺杂的石墨烯纳米带HZGNRs,以及拉伸后的H-ZGNRs进行了结构优化.由于氢原子的间隔吸附掺杂,使得H-ZGNRs的相邻C原子间的相互作用发生改变.相比于未进行掺杂的ZGNRs,优化后的原子结构发生了很大的变化,如图3中插图所示.H-ZGNRs中的C原子起伏变大,并且沿x轴方向上呈锯齿状形态.随后我们为了探讨其结构稳定性,利用公式E=(EH-ZGNRs-EZGNRs-n·EH)/n计算了该结构的C—H单键结合能,其中n为C—H键的数目.计算单键结合能为-1.90 eV,表明H-ZGNRs中的C原子与H原子发生了较强的共价相互作用,该结构较为稳定.该结果与Subrahmanyam等[25]2011年的实验与理论研究结果相符合,他们指出,石墨烯表面最多能吸附原子个数比nH/nC=50%的H原子,且此时H原子的吸附能为-1.48—-2.77 eV/H atom.
接下来我们从H-ZGNRs中C-C六元环的电荷转移分析着手,研究H-ZGNRs结构的压电特性.如表1及图2所示,其中表1中列出的原子位置情况如图2中所示.表1中给出了H-ZGNRs中六元环不同原子的电荷,由于结构的周期性,C2与C6位置、C3与C5位置的电荷一样.另外,C2,C4,C6位置的电荷是C原子与H原子的电荷之和.
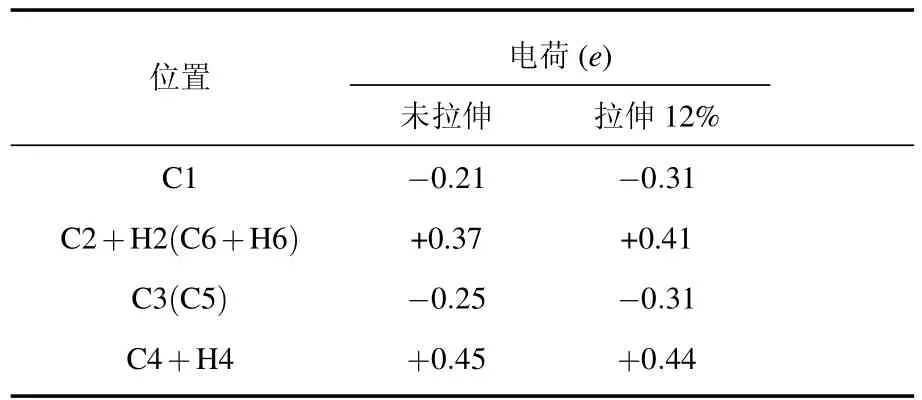
表1 H-ZGNRs六元环不同原子的电荷(对应位置见图2)
从表1中可以明显看出,由于H原子的间隔吸附,C六元环中发生了较大正负电荷转移,相邻C原子表现出电偶极矩.有H原子吸附的位置,C原子与H原子均失电子,形成一个正电荷中心,无H原子吸附的位置C得电子,形成一个负电荷中心(如图2所示).虽然相邻C-C原子不等价,然而未拉伸时,C-C六元环结构的形状并未发生较大改变,其整体正负电荷中心仍然重合,对外表现无宏观电极化.
进一步考虑拉伸带来的结构形变对其中电荷分布的影响.H-ZGNRs沿纳米带生长方向拉伸12%后,由于C—C键长与键角发生改变,引起了原子电荷大小发生了较小改变,但是整体的正负性没有变化.值得注意的是,如图2(b)所示,拉伸后六元环结构的形状对称性发生变化,三个正电位置所成三角形的中心向左偏移,而三个负电位置所成三角形的中心向右偏移,形成环中的电偶极矩,对外表现出明显宏观电极化.

图2 H-ZGNRs六元环结构 (a)无拉伸时情况;(b)拉伸后结构,上图均为俯视图,下图均为侧视图
3.2 2 nm H-ZGNRs电偶极矩密度
我们对H-ZGNRs沿纳米带生长的y方向进行不同形变大小的逐步拉伸(2%,4%,6%,8%,10%,12%),并进行结构优化,来研究其电偶极矩密度变化的规律.电偶极矩密度可以反映整体结构在某一方向上的电极化情况,具体计算公式为
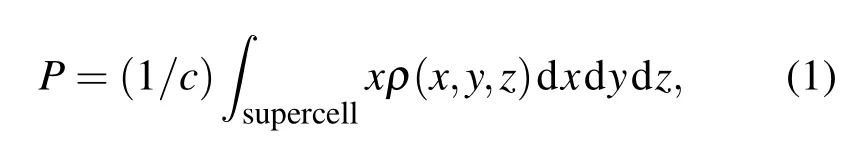
其中,ρ(x,y,z)表示结构整体包括正电荷以及负电荷的总电荷密度,c表示计算结构的晶格周期以及拉伸方向的长度(图1).图3所示为2 nm H-ZGNRs电偶极矩密度P在x方向的分量随拉伸百分比的变化.本文所研究结构的电偶极矩密度矢量在y,z方向均为0,所以下面所以涉及电偶极矩密度的分析均沿x方向.
由图3可知,在没有拉伸时,2 nm H-ZGNRs的电偶极矩密度大于0,为0.81 Debye/˚A.随着拉伸的比率越大,其电偶极矩密度呈单调递减的趋势,当拉伸量达到12%时,其电偶极矩密度从2%时的0.72 Debye/˚A变为0.35 Debye/˚A.这一规律和变化的比率与Qi等[9]研究的BN纳米带的规律类似.
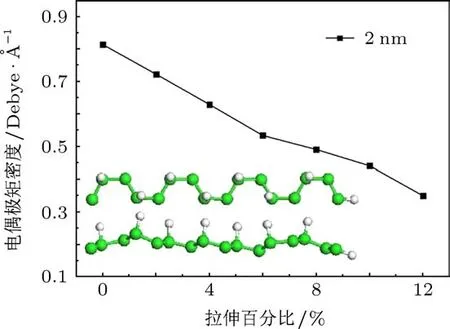
图3 2 nm H-ZGNRs电偶极矩密度P随拉伸百分比的变化规律(左下角插图为优化后的2 nm H-ZGNRs结构)
对于未掺杂的石墨烯纳米带,在没有拉伸时,整体结构不存在电极化现象,P=0.而图3所示2 nm H-ZGNRs结构在没有拉伸时,P>0,说明此时结构已经有x方向的电极化现象.我们首先来分析图1所示的氢修饰结构.在对石墨烯进行间隔性的加氢修饰后,使得靠近最左边边界的C原子有一列没有用氢修饰,而最右边边界的一列C原子却获得了氢的修饰.根据Pauling电负性理论[31,32],C原子的电负性χ(C)=2.55>χ(H)=2.2,电子会从H原子向C原子转移,那么H-ZGNRs结构整体的负电中心会略偏向左边,也就是说此时P>0.而对H-ZGNRs进行y方向的拉伸时,由3.1分析可知,H-ZGNRs结构中的不对称C-C六元环的负电中心会随着拉伸向右边偏移,拉伸量越大,不对称C-C六元环的负电中心向右边偏移越大,所以P值逐渐变小.由此说明,该种氢修饰情况下的石墨烯纳米带H-ZGNRs结构是具有压电性质的.
3.3 不同宽度的H-ZGNRs电偶极矩密度
为了更好地研究拉伸与氢原子修饰对HZGNRs结构压电性能的影响,我们对不同宽度(1,2,3,4 nm)的该种结构进行了一系列电偶极矩密度的研究,结果如图4所示.
由图4所示,在没有进行拉伸时,随着宽度的增加,电偶极矩密度P值逐渐增加.其中,1—4 nm H-ZGNRs结构的P值分别为 0.35,0.81,0.98和1.30 Debye/˚A.可见,随着宽度的增加,整体结构的电极化现象越明显.由3.2的分析可知,H-ZGNRs结构未拉伸时之所以P值不为0,是因为C,H原子电负性不同,以及整体结构的H原子掺杂方式所导致的.而H-ZGNRs结构的宽度越宽,结构中所包含的氢原子数量也就越多,从整体来看,H原子向C原子转移的电荷量也就越多.所以,未进行拉伸时,随着宽度增加,H-ZGNRs的电偶极矩密度P越大.

图4 不同宽度H-ZGNRs电偶极矩密度P随拉伸百分比产生的变化
另外,从图4中可以发现,H-ZGNRs结构宽度越宽,电偶极矩密度减小的趋势越大.其中1 nm H-ZGNRs结构从未拉伸时的0%到拉伸12%过程中的电偶极矩密度P值减小了53%,而其他宽度(2,3,4 nm)下的减小率分别为 57%,59%,62%.这是因为,宽度越宽,H-ZGNRs结构中所包含的不对称C-C六元环越多.那么同等拉伸作用下,不对称C-C六元环形变引起的正负电荷中心的偏移量越大,使得电偶极矩密度P值减小得越大.可见,宽度越宽,H-ZGNRs结构的压电性质越明显.这一结果与Qi等[9]在2012年Nano Letters发表文章中的计算结果非常类似.他们在文中计算了不同宽度(1,2,4,6 nm)边缘氢修饰BN纳米带拉伸前后的电偶极矩密度,同样,氢修饰BN纳米带宽度越宽,拉伸后电偶极矩密度变化越大.其中1 nm宽度情况下,结构从未拉伸的0%到拉伸12%过程中的电偶极矩密度P值增大了66.7%,而其他宽度(2,4,6 nm)下的增大率也随着宽度增加而逐步增大.这一结果也很好地印证了本文对不同宽度H-ZGNRs拉伸后电偶极矩密度变化规律的解释.
3.4 不同氢修饰情况下的H-ZGNRs
由图4发现,不同宽度的H-ZGNRs结构的初始电偶极矩密度呈有规律的变化.同时,Agrawal等[8]在2011年指出,ZnO纳米线自由表面的电荷重新排布而引起的局部极化,将会在很大程度上影响ZnO纳米线的压电性能.也就是说具有压电性质的微观结构,其局部的结构变化往往能有效地调控整体结构的压电性能.因此,接下来进一步探讨H-ZGNRs边缘的不同氢修饰情况下,其初始电偶极矩密度如何变化.在这里以2 nm H-ZGNRs结构为例,对其进行不同方式的氢修饰.如图5所示,A结构表示本文最初采用的修饰方式,B,C结构是在A结构的基础上,去掉了虚线部分的原子,D结构是在A结构基础上增加了虚线框内的H原子,而E结构是在D结构的基础上去掉了正方形虚线框位置上的H原子.随后对这5种模型进行结构优化以及电偶极矩密度的计算,电偶极矩密度的计算结果如图中右边所示.

图5 不同氢修饰模式下2 nm H-ZGNRs结构及其初始电偶极矩密度
图5中,B,C结构的初始电偶极矩密度分别为0.68和0.55 Debye/˚A.B,C结构去掉虚线部分原子之后,与A结构模型的氢修饰模式一样,只相当于在A结构基础上宽度变小了.那么根据3.3中分析的结果,宽度越窄,H-ZGNRs的初始电偶极矩密度P值越小.所以,图5中B,C结构的初始电偶极矩密度P都比结构A略小.另外,B,C结构的P值对比后发现,C结构的P值更小,而B,C结构所去掉的原子数目相同,说明边缘位置C原子的H原子吸附对整体结构电偶极矩密度的影响更大.
对于图5中的D结构,在A结构基础上其最左边一列C原子上吸附了一个H原子,此时P值变为了负数(-0.39 Debye/˚A).这是因为,做D结构所示的改变后,左边失电子的H原子变多,整体结构的电负中心向右边偏移,所以结构D的电偶极矩密度P由原来的正值变为了负值.
最后是图5中的E结构,其初始电偶极矩密度为0.10 Debye/˚A.其中E结构相比于D结构,正方形虚线框所示位置上H原子的失去,使得H-ZGNRs结构左边的H原子密度小于右边.于是,H原子失电子以后,整体结构的电负中心向左边偏移,所以此时P值为正数.同时,该结构整体H原子密度的不平衡,是由于内部C原子上吸附的H原子密度不平衡引起的,因此,其P值较小.
综上所述,H-ZGNRs结构中H原子修饰的方式不同,会导致整体结构的初始电偶极矩密度发生有规律的改变.其中,边缘C原子的H修饰对整体结构电偶极矩密度的影响,比内部C原子影响更大.因此,通过不同的氢修饰方法,可以对H-ZGNRs结构的初始电偶极矩密度进行有效的调控.
4 结论
采用基于密度泛函理论的第一性原理计算,从六元碳环中氢原子吸附的碳原子电荷转移着手,研究了间隔氢吸附锯齿型石墨烯纳米带的压电性质.氢原子的间隔吸附使得有氢原子吸附和无氢原子吸附的碳原子变得不等价,导致石墨烯纳米带的初始电极化状态发生改变.结果表明,间隔氢修饰的石墨烯纳米带具有一定的压电特性.随着宽度增加,拉伸形变产生的正负电荷中心偏移量越大,其电偶极矩密度也随之增大.另外,纳米带边缘的氢原子修饰不仅影响到整体结构的电偶极矩密度,而且能有效调控无拉伸时纳米带的初始电偶极矩密度大小.本文提出的特定氢修饰改性石墨烯纳米带具有压电性能,是一种将石墨烯材料应用于压电领域的有效途径.
[1]Brown C S,Taylor R,Thomas L A 1962 Proc.IEEE B 43 193
[2]Philippot E,Goiffon A,Ibanez A 1994 J.Solid State Chem.110 356
[3]King-Smith R D,Vanderbilt D 1993 Phys.Rev.B 47 1651
[4]Xin J,Zheng Y Q,Shi E W 2007 Appl.Phys.Lett.91 112902
[5]Majdoub M S,Sharma P,Cagin T 2008 Phys.Rev.B 77 125424
[6]Kholkin A,Amdursky N,Bdikin I,Gazit E,Rosenman G 2010 ACS Nano.4 610
[7]Qi Y,Kim J,Nguyen T D,Lisko B,Purohit P K,McAlpine M C 2011 Nano Lett.11 1331
[8]Agrawal R,Espinosa H D 2011 Nano Lett.11 786
[9]Qi J S,Qian X,Qi L,Feng J,Shi D,Li J 2012 Nano Lett.12 1224
[10]Morozov S V,Novoselov K S,Schedin F,Jiang D,Firsov A A,Geim A K 2005 Phys.Rev.B 72 201401
[11]Garcia-Sanchez D,van der Zande A M,Paulo A S,Lassagne B,McEuen P L,Bachtold A 2008 Nano Lett.8 1399
[12]Hu H X,Zhang Z H,Liu X H,Qiu M,Ding K H 2009 Acta Phys.Sin.58 7165(in Chinese)[胡海鑫,张振华,刘新海,邱明,丁开和2009物理学报58 7165]
[13]Santos J E,Peres N M R,dos Santos J,Neto A H C 2011 Phys.Rev.B 84 085430
[14]Wu J B,Qian Y,Guo X J,Cui X H,Miao L,Jiang J J 2012 Acta Phys.Sin.61 073601(in Chinese)[吴江滨,钱耀,郭小杰,崔先慧,缪灵,江建军2012物理学报61 073601]
[15]Miwa R H,Schmidt T M,Scopel W L,Fazzio A 2011 Appl.Phys.Lett.99 163108
[16]Kang Y J,Kang J,Chan K J 2008 Phys.Rev.B 78 115404
[17]Yan J Y,Zhang P,Sun B,Lu H Z,Wang Z G,Duan S Q,Zhao X G 2009 Phys.Rev.B 79 115403
[18]Lusk M T,Carr L D 2008 Phys.Rev.Lett.100 175503
[19]Wang Z Y,Hu H F,Gu L,Wang W,Jia J F 2011 Acta Phys.Sin.60 017102(in Chinese)[王志勇,胡慧芳,顾林,王巍,贾金凤2011物理学报60 017102]
[20]Denis P A 2010 Chem.Phys.Lett.492 251
[21]Akturk O U,Tomak M 2010 Appl.Phys.Lett.96 081914
[22]Lin Q,Chen Y X,Wu J B,Kong Z M 2011 Acta Phys.Sin.60 097103(in Chinese)[林琦,陈余行,吴建宝,孔宗敏2011物理学报 60 097103]
[23]Elias D C,Nair R R,Mohiuddin T M G 2009 Science 323 610
[24]Balog R,Jørgensen B,Nilsson L,Andersen M,Rienks E 2010 Nat.Mater.9 315
[25]Subrahmanyam K S,Kumar P,Maitra U,Govindaraj A,Hembram K P P S,Waghmare U V,Rao C N R 2011 Proc.Natl.Acad.Sci.108 2674
[26]Hohenberg P,Kohn W 1964 Phys.Rev.B 136 864
[27]Kohn W,Sham L J 1965 Phys.Rev.A 140 1133
[28]Portal D S,Ordej´on P,Artacho E,Soler J M 1997 J.Quantum.Chem.65 453
[29]Kohn W,Sham L J 1965 Phys.Rev.A 137 1697
[30]Perdew J P,Zunger A 1981 Phys.Rev.B 23 5048
[31]Pauling L 1932 J.Am.Chem.Soc.54 3570
[32]Allred A L 1961 J.Inorg.Nucl.Chem.17 215
