基于混合粒子群法的RLV上升段轨迹优化
2013-08-22张鼎逆
张鼎逆,刘 毅
(同济大学航空航天与力学学院,上海 200092)
可重复使用运载器(reusable launch vehicle,RLV)轨迹优化问题属于非线性、带有状态约束和控制约束的最优控制问题.与巡航段和再入段不同,大气环境、运动状态以及发动机推力的剧烈变化,使得RLV的上升轨迹呈高度非线性,且受到控制约束、路径约束和端点约束等条件的限制,增加了轨迹优化设计的难度[1-2].优化求解方法的设计是上升段轨迹优化的难点之一,求解的基本思路是用一个或多个有限维子问题来代替无限维的最优控制问题.传统的最速下降法、拟牛顿法和乘子罚函数法等方法被广泛用于最小热载,最大荷载等轨迹优化问题,但普遍存在对初始值敏感等局限性.近年来,序列二次规划法(sequential quadratic programming,SQP)和一些智能优化方法如遗传算法(genetic algorithm,GA)、粒子群算法(particle swarm optimization,PSO)等也越来越多被用来求解轨迹优化问题[3-4].智能算法具有很好的全局搜索性能,但是在局部最优值附近收敛缓慢[5-6].基于梯度的算法在局部搜索方面效率较高,可以获得高精度的解,然而此类方法很大程度上依赖于初始点的选取,可行域的结构和目标函数的类型,不合适的初始点往往导致迭代发散或收敛至局部最优.为了提升算法性能,可以将多种优化策略结合使用来弥补单独使用的不足.如为了避免智能算法结果的抖动现象,往往采用梯度算法做后续计算.这种组合技术通常被称为混合优化方法,并已成功应用于各类工程问题和研究中[7-9].美国德克萨斯大学的 K.Subbarao 和 B.M.Shippey[10]采用混合遗传算法求解了最短时间空间轨道转移问题,通过打靶法和遗传算法能够获得合适的解初值,但是遗传算法在处理空间轨迹问题时明显增加了问题的复杂度.英国南安普顿大学的 J.S.Alsumait等人[11]将GA、模式搜索和SQP的混合算法用于经济学优化问题,对多种方法的混合进行了一系列尝试.
文中根据轨迹优化问题的分析方法、动态系统的离散技术、智能算法与基于梯度算法的混合优化方案等理论,发展一种结合粒子群算法和序列二次规划法的混合优化方法,即HPSO法,并将其应用于RLV上升段的轨迹优化问题中.
1 上升段轨迹优化问题
1.1 飞行运动学方程
RLV上升段属于有动力的爬升飞行,上升过程的状态量和控制量直接决定了巡航和再入的高度和速度等轨迹状态,也间接影响了末端区域能量管理段和自动着陆段的能量控制和轨迹控制.因此,上升段在RLV任务飞行中有着重要的作用,有必要对其进行轨迹优化设计.针对机载空中发射起飞的RLV,假设地球坐标系静止,考虑纵向平面内的三自由度运动,上升段的轨迹模型如下[1]:
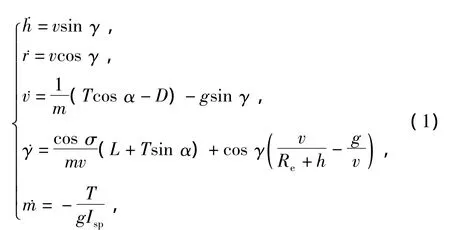
式中:状态向量 X=[h,r,v,γ,m]包括高度 h,航程r,速度 v,航迹角 γ 和质量 m;控制向量 U=[α,σ]包括迎角α,滚转角σ;Re为地球半径;L为升力;D为阻力;T为推力;g为重力加速度;Isp为发动机比冲.
1.2 发动机模型
采用火箭发动机和冲压发动机的组合作为推进系统,以便在不同的马赫数下达到最优推力状态.组合式发动机包括如下2种工作模态:①0≤M≤3,火箭发动机工作;②M>3,冲压发动机工作.
火箭发动机的比冲和推力如图1所示.

图1 火箭发动机比冲和推力
冲压模态下发动机的推力由空气流量˙mair和比冲 Isp决定,如下式[12]:

式中:下标32.5表示该物理量在高度32.5 km处的值;ρ为大气密度;vsound32.5为声速;v32.5为 RLV 速度.冲压发动机在32.5 km的空气流量和比冲如图2所示.


图2 冲压发动机空气流量与比冲
1.3 气动力模型
升力、阻力公式表示为如下标准形式:
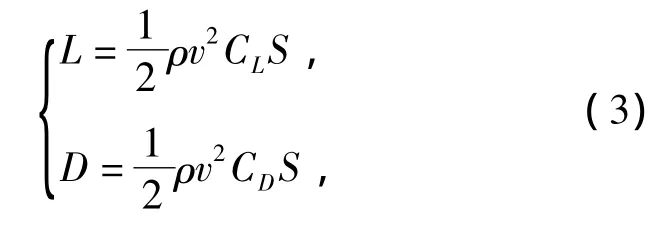
式中:CL为升力系数;CD为阻力系数;S为机翼参考面积.其中CL,CD与M和α的关系如图3所示.

图3 CL,CD与M和α的关系
1.4 约束条件

式中:RN为驻点曲率半径.
2 优化设计方法
本节对最优控制问题的离散预处理,多邻域改进PSO的求解步骤以及HPSO混合策略做简要概述.SQP是一种应用相对成熟的优化方法,其详细方法参考文献[13].
2.1 配点离散
考虑满足运动方程、端点和过程条件等约束的RLV轨迹优化问题为

上式可看作是对无限维状态量X(t)与控制量U(t)的非线性优化,属于泛函优化问题.由于粒子群算法和序列二次规划法的搜索空间是欧几里得空间,所以需要对X(t)和U(t)进行参数离散.文中采用直接配点法将轨迹优化问题转化为多维变量x的非线性NLP,即为

直接配点法是基于连续最优控制系统与离散最优控制系统的变换关系发展而来的,具有严格的数学理论推导[4].
2.2 多邻域改进PSO
传统PSO在处理高复杂度优化问题时存在着粒子信息共享缓慢,速度和位置更新容易超出界限等不足,因此,采用多邻域共享方案,时变惯性因子和粒子限速等策略对传统方法进行改进,可有效改善PSO的优化性能.
在n维搜索空间中,m个粒子组成一个群体,每个粒子pi具有位置xi和速度vi等属性,其中:xi=(xi1,xi2,…,xij,…,xin),vi=(vi1,vi2,…,vij,…,vin),1≤i≤m,1≤j≤n.
运用多邻域改进PSO计算非线性规划问题的初始值,算法步骤如下[14]:
1)初始化
2)邻域划分
将群体划分成多个邻域,邻域内的粒子共享此邻域信息,特定粒子传递全局信息至其他邻域,从而既保证了粒子搜索的独立性,也容易得到全局最优解.
3)适应度计算与处理
令pbest,i为第i个粒子的历史最优值;gbest为群体的历史最优值;plbest,l为第l个邻域的历史最优值.通过适应度函数计算各粒子的适应度值并进行最优值的统计与更新.
4)速度更新
按照如下公式计算速度:

式中:w为速度惯性因子;c1,c2,c3为学习因子,通常取c1=c2=c3=2;εrand为0和1之间的随机数.采用时变惯性因子,即迭代初期w取值较大,随着各粒子适应度的接近而逐渐减小:

式中:kmax为最大迭代次数;k为当前迭代次数.如果在最优点附近速度较大,粒子将飞离最优点,所以根据优化状态对w做进一步处理:

如果粒子的适应度值变优,速度将按照原有的惯性进行更新;若适应度值变差,降低粒子速度以提高局部搜索能力.
Ti为学习能力函数,用于判别粒子获取全局或邻域知识的能力,Ti的表示为
试验的荷载(p)-沉降(s)曲线如图3、图4所示。在较低的荷载范围内(200 kPa),地基基本处于弹性变形状态。
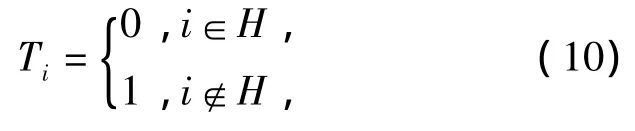
式中:H为可以获取全局知识的粒子集合.
5)位置更新
按照如下公式计算位置可以起到限速作用,并且不会丧失粒子的搜索能量:

对于超出位置限制的粒子,通过如下公式可以满足位置区间约束:
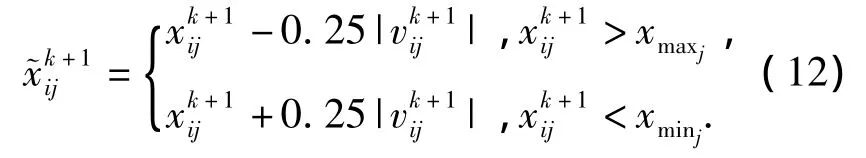
当粒子位于局部最优点附近时,速度的大幅衰减可导致其搜索能量的不足,采用变异率σ进行位置的随机更新,可使粒子重新获得搜索能力.速度判别函数与位置更新函数如下:

式中:σ∈[0,1];常数τ是最小速度限制,大小和问题的求解精度有关.
2.3 HPSO混合策略
HPSO混合算法的计算步骤如下:首先利用PSO的突变性搜索全局初始最优解,当不满足问题精度时,跳出局部极值点继续迭代计算;当达到PSO终止条件后,利用SQP的数值解析计算得到更优的最终值.PSO和SQP分别进行优化计算,不仅迭代结果优于PSO算法得到的初始解,而且提高了收敛速度和计算精度.HPSO的算法流程如图4所示.

图4 HPSO流程图
3 上升轨迹优化问题
3.1 最小燃料消耗问题
考虑DeltaIII运载火箭的上升段轨迹优化问题,目标函数为 max J=mf,状态向量 X=[r,v,m]包括位置r,速度v和质量m.控制向量 U=[ux,uy,uz]为推力矢量.运动方程、设计参数、动力参数和气动参数等详见文献[15].
经过多次计算,取离散配点数20,PSO群体规模20,邻域数3,最大最小惯性因子分别取0.7和0.1,位置变异率 0.01,迭代终止的误差阀值设为10-6.表1为各算法的计算时间和最优值比较.

表1 各次主要计算结果比较
HPSO法与文献[15]以及单独采用SQP的计算结果比较见图5.

图5 状态与控制变量曲线
由图5可见,HPSO的优化结果与文献[15]近乎重合,可以看出该算法的优化精度很高.而SQP在没有合适初始估计的情况下,结果相对较差.仿真结果表明,HPSO法优化的轨迹满足约束条件和目标函数要求,并且在计算精度和效率上较SQP有了较大提高.
3.2 RLV亚轨道上升问题
上升段的高度、速度和迎角等参数对巡航以及再入有很大影响,速度越高表示飞行动能越大,入轨所需动力越少;高度越高,则其飞行势能越大,入轨所需动力也越少;而迎角则是需要优化的参变量.如何最大程度增加上升段RLV的有效载荷,是总体设计和性能分析的重要研究点.除了通过改进动力装置和采用轻型材料2种途径以外,在起飞重量恒定的条件下还可通过减少燃料消耗来实现.
RLV上升段的初始与末端条件如下:h(t0)=9 km,v(t0)=238 m·s-1,γ(t0)=4°,h(tf)=32 km,v(tf)=2240 m·s-1,γ(tf)= -1°.
给出状态量与控制量的有效范围如下:-45°≤γ≤45°,-45°≤α≤45°,-45°≤σ≤45°.
设热流密度、动压和过载约束分别为420 kW·m-2,29 kPa 和2.5g.初始总重 m0=5000 kg,机翼参考面积S=12 m2,驻点曲率半径RN=0.25 m.海平面大气 密度 ρ0=1.225 kg·m-3,大 气常量 β =0.000137.
取离散配点数n=30,HPSO的群体规模100,迭代次数20000.计算的末端重量mf为3272.6 kg.轨迹上升时间为218.74 s,部分状态和控制曲线如图6所示.
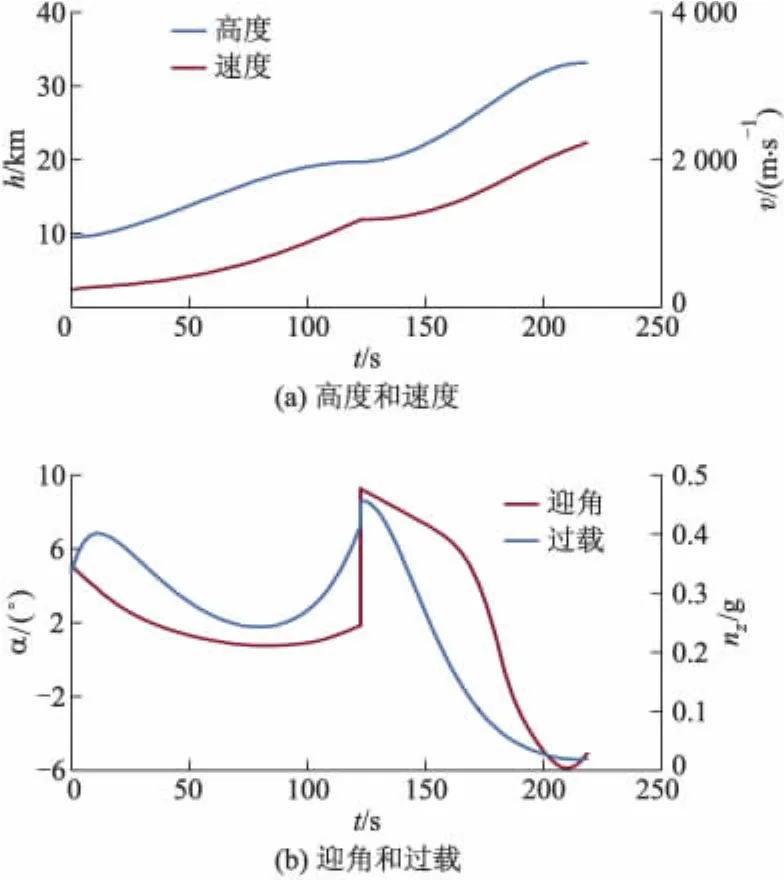
图6 上升轨迹曲线
由图6a高度曲线可见,火箭发动机工作位于9~16 km的高度范围内,随后进入冲压发动机的大推力状态,高度为16~32 km.上升末端高度空气稀薄,冲压推力处于较小值,此时不能产生足够的加速度,因此高度变化趋于平缓.由图6a速度曲线可见,由于忽略了动力转换的过渡段,火箭动力结束后速度曲线存在着一个拐点,拐点前后具有不同的加速度斜率.从高度和速度的曲线看出,到达末端高度时,速度为2240 m·s-1,高度为32 km,满足上升段末端条件.由图6b迎角控制曲线可见,发动机点火时迎角较大,随着飞行过程中高度增加,迎角逐渐减小以有利于RLV的姿态控制,从而可以平滑过渡到下一阶段.同时,控制迎角满足约束以防止上升率过大,否则容易影响RLV的操纵性和稳定性.由图6b过载曲线可见,升力L和阻力D随着迎角的增大而增加,法向过载也随之增大.两次点火位置对应的局部迎角相对最大,因此局部最大过载也发生在这两点.
4 结论
1)HPSO法不需要指定初始迭代点,SQP所需的合适初始估计由PSO优化阶段自动获得,因此克服了SQP对初始估计过分依赖的缺点,避免了对初值敏感而导致陷入局部极值.随着优化系统规模和复杂度的增加,HPSO算法的这个特点更是显而易见的.
2)HPSO法可以得到更优的数值解,并且能有效缩短计算时间,减少大尺度复杂优化问题的计算量.
3)对RLV上升段轨迹优化问题的计算表明文中的混合算法可以很好地解决工程优化问题.
References)
[1]Hirschel E H,Weiland C.Design of hypersonic flight vehicles:some lessons from the past and future challenges[J].CEAS Space Journal,2010,1(1/2/3/4):3-22.
[2]Williams P.Hermite-Legendre-Gauss-Lobatto direct transcription in trajectory optimization[J].Journal of Guidance, Control, andDynamics, 2009, 32(4):1392-1395.
[3]Huntington G T,Rao A V.Comparison of global and local collocation methods for optimal control[J].Journal of Guidance,Control,and Dynamics,2008,31(2):432-436.
[4]Jain S,Tsiotras P.Trajectory optimization using multiresolution techniques[J].Journal of Guidance,Control,and Dynamics,2008,31(5):1424 -1436.
[5]Wuerl A,Crain T,Braden E.Genetic algorithm and calculus of variations-based trajectory optimization technique[J].Journal of Spacecraft and Rockets,2003,40(6):882-888.
[6]Pontani M,Conway B A.Particle swarm optimization applied to space trajectories[J].Journal of Guidance,Control,and Dynamics,2010,33(5):1429 -1441.
[7]Fesanghary M,Mahdavi M,Minary-Jolandan M,et al.Hybridizing harmony search algorithm with sequential quadratic programming for engineering optimization problems[J].Computer Methods in Applied Mechanics and Engineering,2008,197(33/…/40):3080-3091.
[8]Sentinella M R,Casalino L.Cooperative evolutionary algorithm for space trajectory optimization[J].Celestial Mechanics& Dynamical Astronomy,2009,105(1/2/3):211-227.
[9]Vavrina M A,Howell K C.Global low-thrust trajectory optimization through hybridization of a genetic algorithm and a direct method[C]∥Proceedings of AIAA/AAS Astrodynamics Specialist Conference and Exhibit.Reston:American Institute ofAeronauticsand Astronautics Inc.,2008,article number:2008 -6614.
[10]Subbarao K,Shippey B M.Hybrid genetic algorithm collocation method for trajectory optimization[J].Journal of Guidance,Control,and Dynamics,2009,32(4):1396-1403.
[11]Alsumait J S,Sykulski J K,Al-Othman A K.A hybrid GA-PS-SQP method to solve power system valve-point economic dispatch problems[J].Applied Energy,2010,87(5):1773-1781.
[12]Prasanna H M,Ghose D,Bhat M S,et al.Interpolationaware trajectory optimization for a hypersonic vehicle using nonlinear programming[C]∥Proceedings of Collection of Technical Papers-AIAA Guidance,Navigation,and Control Conference.Reston:American Institute of Aeronautics and Astronautics Inc.,2005:2160 -2171.
[13]谢 政,李建平,陈 挚.非线性最优化理论与方法[M].北京:高等教育出版社,2010.
[14]杨雪榕,梁加红,陈 凌,等.多邻域改进粒子群算法[J].系统工程与电子技术,2010,32(11):2453-2458.Yang Xuerong,Liang Jiahong,Chen Ling,et al.Multineighborhood improved particle swarm optimization algorithm[J].Systems Engineering and Electronics,2010,32(11):2453-2458.(in Chinese)
[15]Benson D.A Gauss pseudospectral transcription for optimal control[D].Cambridge:Massachusetts Institute of Technology,2005.
