平面桁架内力求解的“奇怪”现象分析

程燕平，王春香

(哈尔滨工业大学航天科学与力学系，哈尔滨150001)

理论力学是高等工科重要的技术基础课，也是工程文化素质培养的重要内容之一，学生对课程基本理论、基本方法及基本概念是否真正理解掌握，直接影响他们的逻辑思维能力和解决工程实际问题的能力.

1 教学中遇到的问题

对学过理论力学的人，可谓众所周知，平面任意力系有三个独立的平衡方程，因在所有理论力学教材[1－5]中，均给出这样的结论[6].但在某些情况下，却会出现特殊情况.笔者在教学中，就多次遇到学生问这样的问题.在哈工大《理论力学》第4版至第7版中，均有求平面桁架内力的两个题目，如第7版78页题2－55中，取整体为研究对象，其受力图如图1所示，此为一平面任意力系，列3个平衡方程可求出支座A处与B处3个约束力.具体列平衡方程并求解如下(设AD=DB=l):

∑MA=0 FNB·2l－F·lsin60°=0 解得

∑Fix=0 FAx+F=0 解得 FAx=－F

∑Fiy=0 FAy+FNB=0 解得

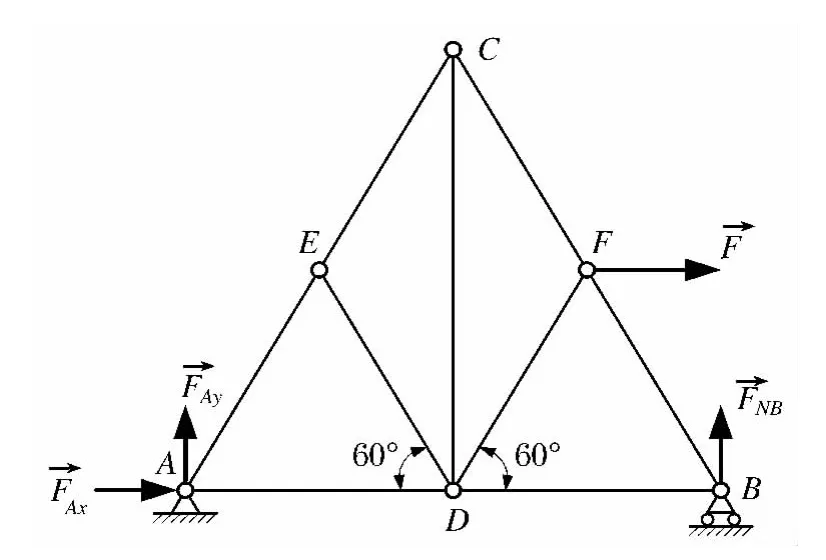
图1 整体为研究对象

为求杆CE，CD，CF的内力，采用截面法，截断CE，CD，CF杆，取研究对象如图2所示，这显然是一个平面任意力系，而此平面任意力系有3个未知数，列3个平衡方程可求出3根杆受力F1，F2，F3，如列平衡方程如下:

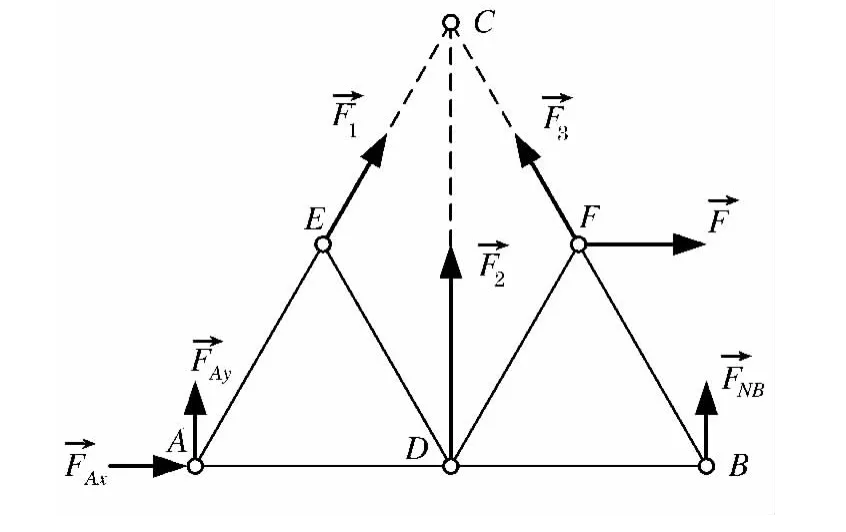
图2 部分为研究对象

但无论如何求解这3个方程也求不出3个未知力 F1，F2，F3.为此，许多学生感到很迷惑，明明是一个平面任意力系，列出的3个平衡方程也无错误，但为什么就求不出3个未知力呢?笔者在教学中经常遇到学生问这样的问题.实际上，不但学生多次问过这样的问题，一些比较年轻甚至比较年长的老师也和笔者讨论过这样的问题.

同样还有另一个题目，如第7版78页求解题2－58也是这种情况.取整体为研究对象，其受力图如图3所示，此为一平面任意力系，列3个平衡方程可求出支座A处与B处3个约束力，具体列平衡方程并求解如下:

∑MA=0解得

∑Fix=0 FAx=0 解得 FAx=0

∑Fiy=0 FAy－F+FNB=0 解得

图3 桁架整体研究受力图

为求杆DA，DF，DC的内力，采用截面法，截断DA，DF，DC杆，取研究对象如图4所示，这显然是一个平面任意力系，而此平面任意力系有3个未知数，列3个平衡方程可求出3根杆受力 F1，FFD，FAD，列平衡方程如下:

图4 桁架部分研究受力图

但无论如何求解这3个方程也求不出3个未知力 F1，FFD，FAD.明明是一个平面任意力系，列出的3个平衡方程也无错误，但为什么就求不出3个未知力呢?对此题，类似的可取受力图如图5所示，这也明明是一个平面任意力系，有兴趣的读者可列出3个平衡方程求解，但也肯定求不出3个未知力.

2 解释

上面所提出的问题很多学生感到“奇怪”、疑惑与不解，实际上一些老师也感到疑惑与不解，明显是一个平面任意力系，列出的3个平衡方程也无错误，但为什么就求不出3个未知力呢?

平面任意力系有3个独立的平衡方程，但对这两个桁架题目，图2、4、5表面上看起来是一个平面任意力系，但实际上是一个平衡的平面任意力系和一个平衡的平面汇交力系的叠加.图2是图1的平面任意力系和一平面汇交力系组合而成，图4或图5是图3的平面任意力系和一平面汇交力系组合而成.所以，图1、2合起来，图3、4(或图5)合起来，实际上是一个平面任意力系和一个平面汇交力系的组合，两受力图合起来，独立的平衡方程为5个，而不是6个.这个问题不但对这两个桁架题目成立，而且具有普遍意义.对物体系的平衡问题，当取整体(或某一部分)为一平面任意力系时，称此力系为力系Ⅰ，见图6，图6中只画出了3个未知力F1，F2，F3其余的力没有画出.其独立平衡方程为3个，若为静定问题，可求出这3个未知力.当取一部分物体为研究对象，包含力系Ⅰ，同时又暴露出3个未知力F4，F5，F6，且这3个未知力汇交于一点，设为H，见图7，其余的力也没画出.这3个未知力和力系Ⅰ又组成一平面任意力系，称为力系Ⅱ，力系Ⅱ看起来是一平面任意力系，但在F1，F2，F3已知的情况下，此平面任意力系只有2个独立的平衡方程，相当于一平面汇交力系.因为力系Ⅱ是平衡力系，对任意点的力矩和为0，未知力 F4，F5，F6的汇交点H，也为任意点中的一个，对汇交点H取矩，方程∑MH=0中包含力系Ⅰ对点的力矩和为0，而未知力F4，F5，F6对H点的力矩均为零，在此方程(∑MH=0)中无未知力出现，而已用去一个方程，因此，独立的平衡方程为两个，而不是3个.另一类同的解释是，可以认为力系Ⅱ是力系Ⅰ与平面汇交力系的组合，而力系Ⅰ是平面任意平衡力系，剩下的为平面汇交力系，所以其独立的平衡方程为2个而不是3个.

图5 另一部分受力图

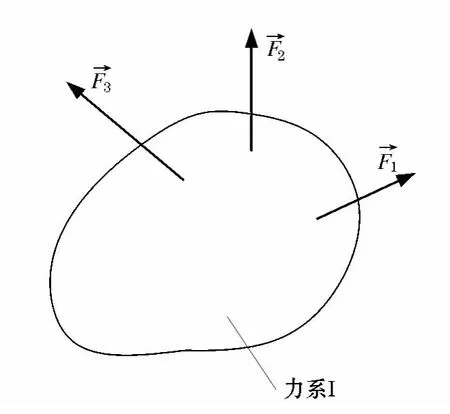
图6 整体为平面任意力系

图7 部分也为平面任意力系

3 结语

总之，在静力学中，当取一研究对象，此研究对象受平面任意力系作用时，若为静定问题，列3个平衡方程可求出3个未知数，若在此研究对象中再拆去某些构件，而暴露出3个未知力，且此3个力汇交于一点，此时看是一任意力系，有3个独立的平衡方程，两个研究对象表面上有6个独立的平衡方程，但实际上，两个研究对象只有5个独立的平衡方程.此结论也可推广至空间力系.

从图7可以看出，在剪状态下，孔边补强对于减少腹板上的应力集中有很好的效果.在纯剪状态下，包边补强是最优的选择，并且在保证补强片不增大脱胶时，补强结构的刚度，有利于减小腹板的应力集中的效果，与Guo S等[9－10]研究结论一致.

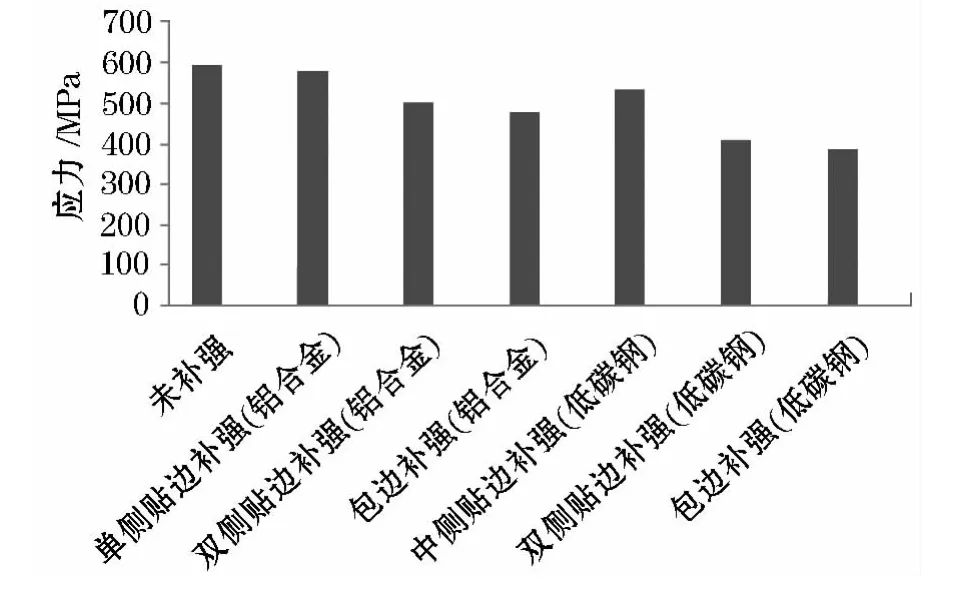
图7 孔边最大应力值

5 结论

本文通过数值模拟方法研究了复合材料开孔工字梁在剪切力作用下孔边应力及补强分析，讨论了开孔间距，开孔距离梁下缘条的高度及开孔形状对孔边应力分布的影响，并针对水滴型孔研究了三种补强方式对孔边应力水平的影响.得到了以下结论:

1)开孔间距、开孔距离梁下缘条的高度及开孔形状对孔边应力集中程度都有影响，但是开孔距离梁下缘条的高度和开孔形状影响较大.2)圆孔孔边的最大应力比水滴型孔边的最大应力高出15.58%，因此，从降低孔边应力水平考虑，水滴型孔优于圆形孔.开孔高度为3、11 mm时，应力幅值都比高度为7 mm时略高，随着高度增加，孔边应力先减小后增大.随着孔间距的增大，腹板上的应力幅值逐渐降低.3)补强能降低开孔处的应力，提高结构承载能力.包边补强效果最好，双侧贴片补强次之，单侧贴片补强效果最弱.补强材料刚度越大，补强效果越好.

[1]ZEMLYANOVA A Y，SILVESTROV V V.The problem of the reinforcement of a plate with a cutout by a two－dimensional patch[J].Journal of Applied Mathematics and Mechanics，2007，71(1):40－51.

[2]LIU Y，JIN F，LI Q.A strength－based multiple cutout optimization in composite plates using fixed grid finite element method[J].Composite Structures，2006，73(4):403 －412.

[3]张 斌，黄上恒，宋辉辉，等.孔口缝合补强对含孔复合材料层板应力集中影响的数值模拟[J].应用力学学报，2009，26(4):804－807.

[4]提亚峰，张 铎，孙宏杰，等.在轴、外压联合作用下的C/E复合材料网格缠绕结构的开口补强设计[J].宇航材料工艺，2010，40(6):27－32.

[5]童 瑶，刘兴宇，刘衰财.复合材料腹板开口补强设计及有限元分析[J].民用飞机设计与研究，2009(4):30－33，43.

[6]商 霖.复合材料层合板开口的非对称补强研究[J].导弹与航天运载技术，2009(4):40－43.

[7]王 毅.复合材料开口补强实验研究和设计分析[D].西安:西北工业大学，2006.

[8]喻 梅.复合材料结构挖补补强强度研究[D].南京:南京航空航天大学，2005.

[9]GUO S，MORISHIMA R，ZHANG X，et al.Cutout shape and reinforcement design for composite C－section beams under shear load[J].Composite Structures，2009，88(2):179 －187.

[10]余建新，陈立平.复合材料结构阻尼测试分析[J].哈尔滨商业大学学报:自然科学版，2011，27(5):729－732.