一类具有垂直传播的HIV模型最优控制问题

张 瑜，任泽洙，孙李红

(1.哈尔滨商业大学基础科学学院，哈尔滨150028;2.哈尔滨商业大学经济学院，哈尔滨150028)

艾滋病(AIDS)全称为“获得性免疫缺陷综合症”，是一种由人体免疫缺陷病毒(HIV)所引起的以全身免疫系统严重损害为特征的传染性疾病.自1981年在美国发现首例艾滋病病例后，艾滋病在全球范围内迅速蔓延.据《联合国艾滋病规划署2011年世界艾滋病日报告》，截至2010年底，全球共有3400万(3160万～3520万)名艾滋病感染者，其中2010年新发感染270万例(240万～290万)，180万人(160万～190万)死于艾滋病相关原因[1].而中国自1985年报告首例艾滋病至今，艾滋病病毒感染者迅速增加.截至2011年底，估计全国存活艾滋病病毒感染者和艾滋病病人78万人(62～94万人)，其中2011年新发HIV感染者4.8万人(4.1 ～5.4 万人)，艾滋病相关死亡 2.8 万人(2.5～3.1万人).2011年疫情估计结果提示在我国艾滋病呈现感染人群多样化，流行形势复杂化的趋势，且仍有大量的HIV感染者和AIDS病人尚未被发现，存在进一步传播的危险[2].

目前，关于艾滋病动力学模型的相关研究很多[3－6]，但多数为对模型平衡点的稳定性分析，对传播模型的最优控制问题却鲜有研究.本文在文献[3]的基础上，将有效接触率作为控制变量，讨论一类具有垂直传播的HIV模型的最优控制问题，用范数指标函数作为衡量控制变量的标准得出该模型最优控制元的存在惟一性.

1 具有垂直传播的HIV模型

将HIV携带者分为成年和幼年2类，建立如下模型[3]:

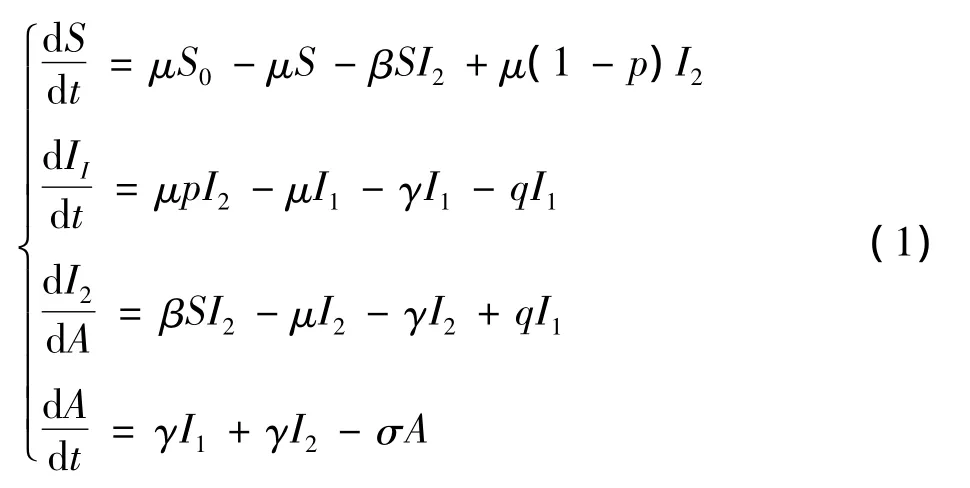
其中:S为易感者;I1为HIV病毒的幼年携带者者;I2为HIV病毒的成年携带者;A为艾滋病患者;μ表示个体的自然死亡率和成年HIV携带者对婴儿的出生率;μS0表示易感者的输入率;β表示HIV病毒成年携带者与易感者之间的有效接触率;p表示垂直传播率;γ表示HIV携带者向艾滋病患者的转化率;σ表示艾滋病患者的死亡率(σ＞μ);q表示幼年HIV携带者向成年HIV携带者的转化率.

文献[3]求出了模型的基本再生数，证明了无病平衡点和地方病平衡点的存在性和全局稳定性，本文在此基础上将继续讨论模型的最优控制问题.

2 具有垂直传播的HIV模型的最优控制问题

由于系统的前三个方程不显含变量A，因此仅需考虑系统

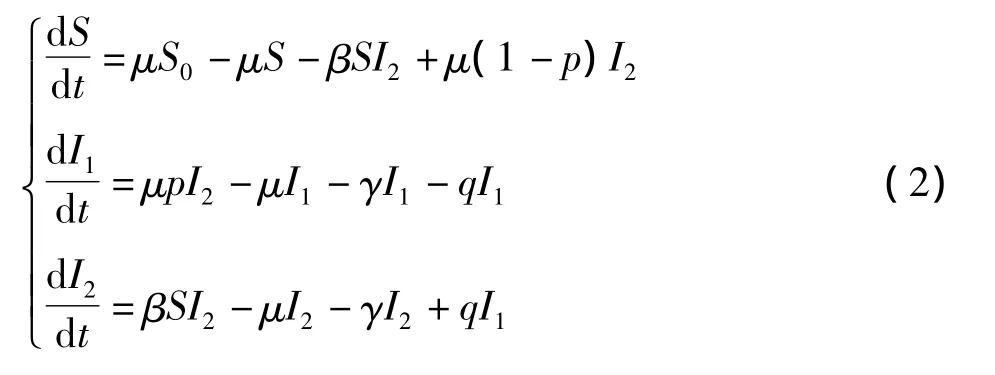
我们在平衡点E0(S0，0，0)处，将方程组系统线性化，令:

x(t)=S(t)－ S0，y(t)=I1(t)，z(t)=I2(t)

则方程组系统化为如下形式:

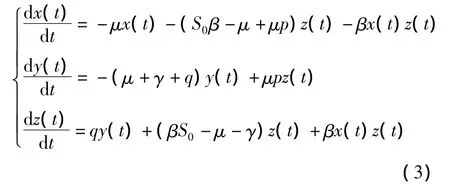
当(x(t)，y(t)，z(t))T→0时，方程组系统右边的二次项都是的高阶无穷小.所以在(0，0，0)T附近，方程组系统解的性态与线性方程组解的性态一致.

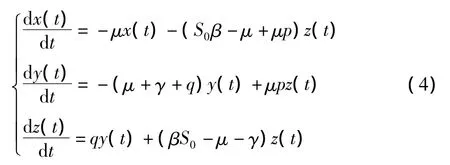
考虑到传染病传播的实际情况，在一定时间内接触率β应与时间有关，故设β=β(t).并给系统方程组加上初始条件(x(t0)，y(t0)，z(t0))T=(x0，y0，z0)T，以下我们讨论有效接触率为β(t)的传播系统的最优控制问题.

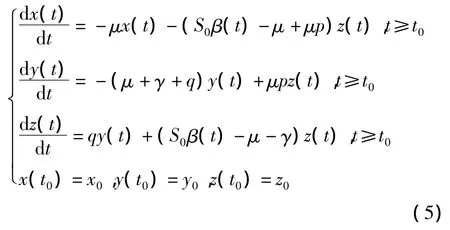
令 X(t)=(x(t)，y(t)，z(t))T，X0=(x0，y0，

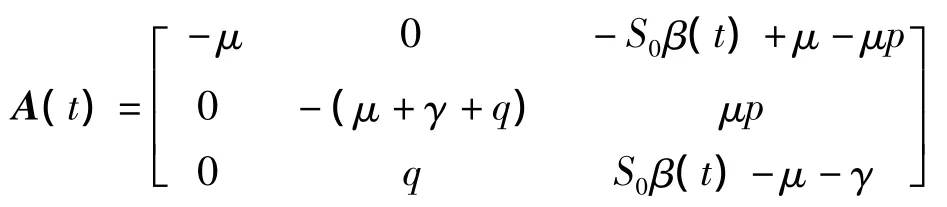
则方程组可写为:

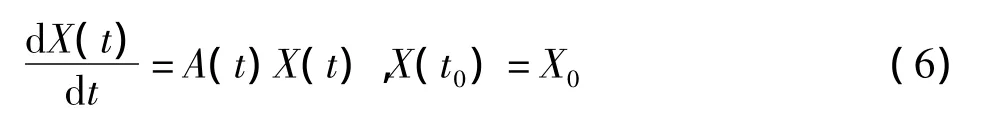
设T＞0，记控制集为:

U={β(t)∈C(0，T)|0≤β(t)}≤M，0≤t≤T，M ＞

0}.在U 中取 L2(0，T)范数，则 U 为 L2(0，T)的闭凸集，取Sobolev空间:L2([0，T];R3)}W1，2([0，T];R3)中范数为:为R3的欧氏范数 由 Sobolev嵌入定理，W1，2([0，T];R3)可看成 L2([0，T];R3)的完备子空间.

β(t)∈U对，我们可知方程的解是惟一存在的.我们在状态空间 W1，2([0，T];R3)中讨论传播系统方程的最优控制问题.设预期状态为X*=(x*，y*，z*)T，指标范函 J为:

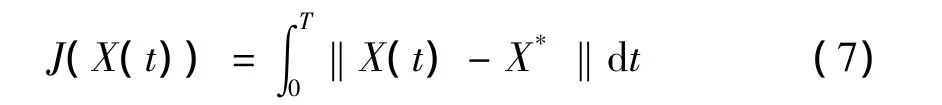
取集合W:

W={X(t)W1，2([0，T];R3)|存在 β(t)∈U，解得 X(t)方程(6)关于 β(t)的解，δ≤y(t)，z(t)≤

具有垂直传播的HIV模型的最优控制问题就是求β0∈U使与之相应的解X0(t)∈W满足:

β0(t)叫传播系统的最优控制元.

定理1 W是L2([0，T];R3)上的闭凸集.

证明 先证W是L2([0，T];R3)上的凸集

设X1(t)，X2(t)∈W由W的定义知存在β1(t)，β2(t)∈U 使得:

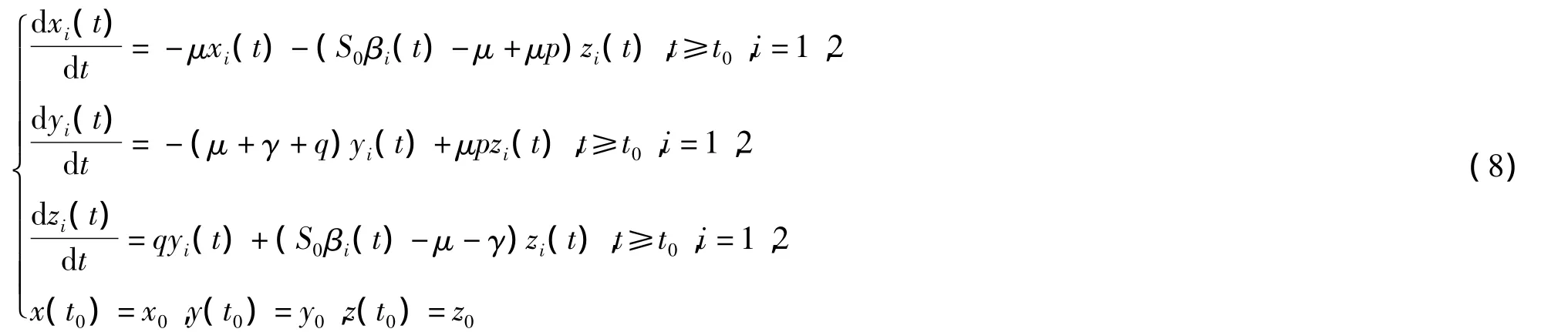
对∀λ(0≤λ≤1)，令 X(t)=λX1+(1 －λ)X2，则:

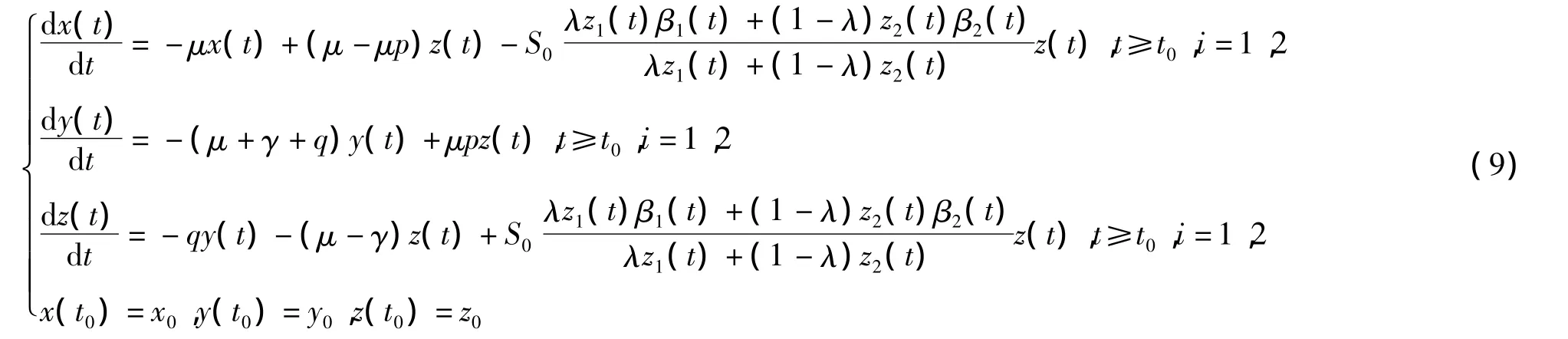
再证W是L2([0，T];R3)上的闭集.

任取序列Xk(t)∈W，满足:

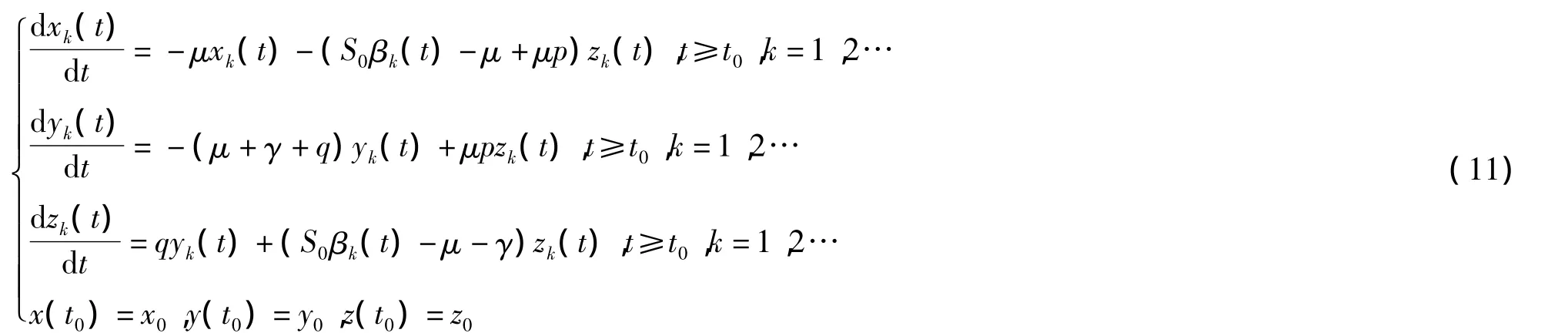
由式(11)中第3式得:

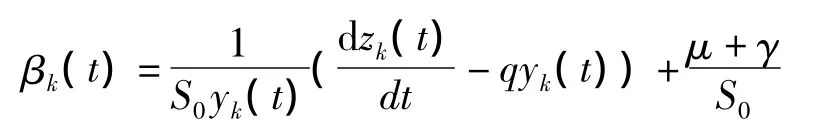
于是{β(t)}为 L2(0，T)中的柯西列，从而是收敛的.记:

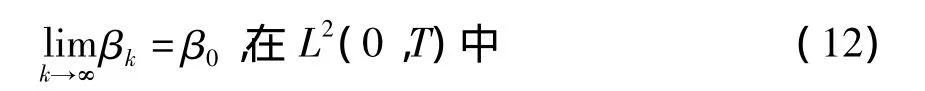
利用式(10)、(12)，对式(11)中第2式两端取极限，得:

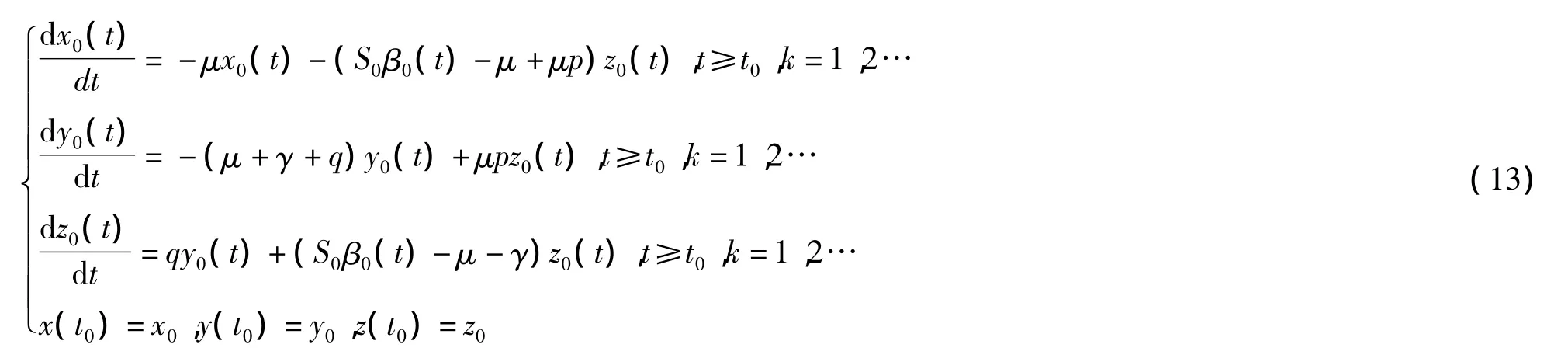
这说明 X0(t)=(x0(t)，y0(t)，z0(t))T是方程组的对应于 β0(t)的解，从而 X0(t)∈W.闭集证毕.

定理2 设X*给定，则传播系统(6)在U中存在惟一的最优控制元.

证明 设{Xk(t)}⊂W是式(7)的极小化序列，即

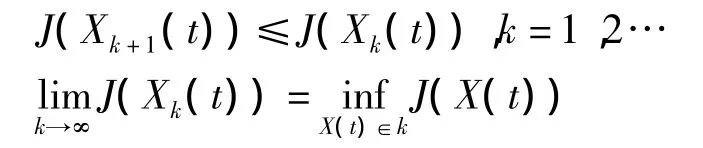
由于Xk(t)相对应U中的控制元为β(t)，所以由解对参数函数的连续依赖性，当β(t)在有界集U中取值时，W也为有界集，而W为空间L2([0，T];R3)上的有界闭凸集，所以能从Xk(t)中选出子列(不妨选其自身)，使得

由Mazur定理，存在(Xk(t))组合序列

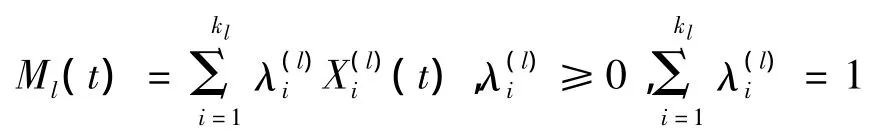
使得

设U中与Ml(t)相应的控制元β(l)(t)，同定理1中闭性证明一样，可得β(l)(t)在L2(0，T)中收敛于β0(t)，于是β0(t)∈U且X0(t)为方程组(6)的解，因为 J 为空间 W1，2([0，T];R3)的范数积分函数，所以J为严格凸函数，又由于{Xk(t)}⊂W是极小化序列，有

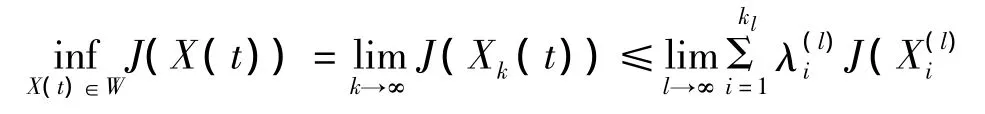
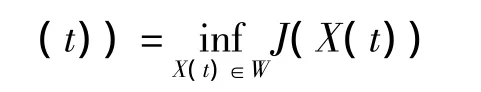
即β0(t)是方程组在中的一个最优控制元[7]，最后由J的严格凸性可知β0(t)是惟一的.定理得证.

3 结语

本文针对一类具有垂直传播的HIV模型，在文献[3]已讨论了各平衡点的存在性及全局稳定性的基础上，讨论模型的最优控制问题，将有效接触率作为控制变量，用范数指标函数作为衡量控制变量的标准得出该模型最优控制元的存在惟一性.

[1]联合国艾滋病规划署.2011年世界艾滋病日报告——全球流行情况[EB/OL].http://www.unaids.org.cn/cn/index，2012－09－30.

[2]中华人民共和国卫生部，联合国艾滋病规划署，世界卫生组织.2011年中国艾滋病疫情估计[J].中国艾滋病性病，2012，18(1):1－5.

[3]张 梅，张凤琴，刘汉武.一类具有垂直传播的HIV模型的稳定性分析[J].工程数学学报，2012，29(3):399－404.

[4]LOU J，MA Z E，SHAO Y M，et al.Modeling the interaction of T cells，antigen presenting cells and HIV －1 in vivo[J].Computers and Mathematics with Applications，2004，48(1－2):9－33.

[5]NELSON P W，PERELSON A S.Mathematical analysis of delay differential equation models of HIV －1 infection[J].Math Biosci.，2002，179(1):73 －94.

[6]李建全，杨亚莉，王 伟.一类带有治疗的HIV传播模型的定性分析[J].工程数学学报，2009，26(2):226－232.

[7]王 辉，金鸿章.可修复复杂系统脆性故障的研究[J].数学的实践与认识，2007，37(19):105－111.