基于突变级数法的突发自然灾害风险等级评价

刘春梅

(哈尔滨商业大学基础科学学院，哈尔滨150028)

我国是一个多种自然灾害频发，灾情损失严重的国家之一，经常发生洪水、地震、台风、泥石流、生物灾害等自然灾害.如:2008年汶川地震，2010年青海玉树地震等.尽管我国政府及相关组织采取了减灾救灾的措施，但这些自然灾害严重影响了社会经济的稳定与发展.自然灾害发生的严重程度的确定关系到能否对各种突发性事件进行控制与决策，因此，对突发的自然灾害风险等级评估与预测是形势发展变化的急需，也是我国目前的自然灾害防范与治理所面临的重要课题.

目前评价自然灾害风险的常用方法有:集对分析法、主成分分析法、聚类分析法和投影寻踪法、灰色关联、AHP 等[1－5].然而，鉴于自然灾害风险评价系统的复杂性与及时性，更应考虑应急物流的时效性，因此本文尝试采用适合系统分析的突变级数法对自然灾害风险等级进行评价，旨在为突发自然灾害风险等级评价提供一种新的思路.突变级数法的主要特点是不需要对指标采用权重，但它考虑了评价指标间的相对重要性.自然灾害的发生就是一种典型的突变现象，所以本文采用突变理论对各受灾地区的影响程度进行评价研究.

1 突变级数法评价原理和基本步骤

1.1 建立突变评价指标体系

首先，对评价总指标进行多层次矛盾(分组)，排列成倒立树状目标层次结构，由评价总指标到下层指标，逐渐分解到下层子指标，原始数据只需要知道最下层子指标的数据就可以了.一个指标进行分解，分解到一般可以计量的子指标时，分解就可以停止.

1.2 确定突变评价指标体系的突变系统类型

突变系统类型中最常见的有3个[6－8]，即尖点突变系统、燕尾突变系统、蝴蝶突变系统，其数学模型分别为:

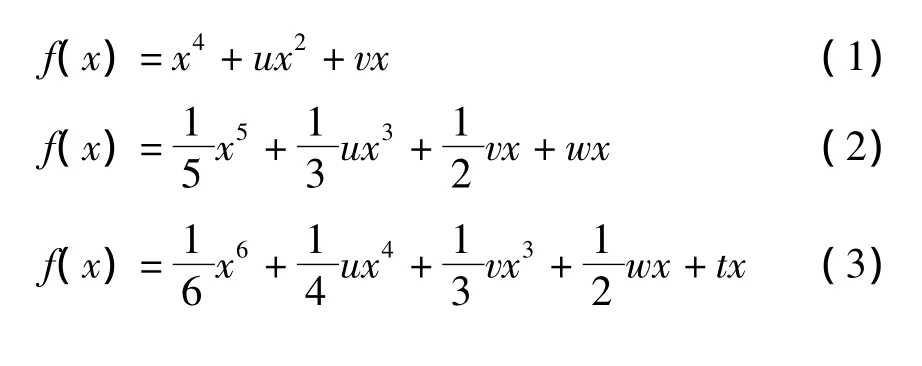
其中:x表示突变系统中的一个状态变量;f(x)表示状态变量x的势函数;u，v，w，t表示状态变量的控制变量.系统势函数的状态变量和控制变量是相互矛盾的两个方面，将控制变量按由主到次的先后顺序写出.突变系统主要分为点突变系统、燕尾突变系统和蝴蝶突变系统.

1.3 确定控制变量归一公式

根据突变理论[7]，尖点突变的归一公式为:

燕尾突变系统的归一公式为:

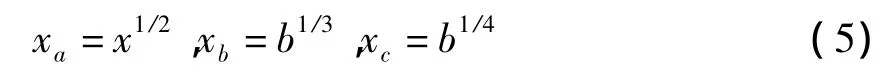
蝴蝶突变系统的归一公式为:

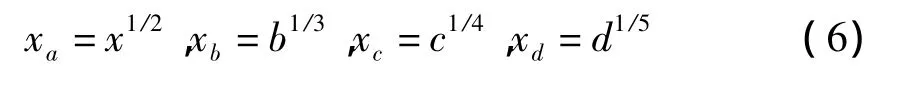
1.4 利用归一公式进行综合评价

根据初始模糊隶属函数值，按归一公式可计算出各控制变量的相应中间值，即突变级数值.因而利用归一公式对同一对象各个控制变量计算出的对应的值应采用“大中取小”原则，但对存在互补性的指标，通常用其平均数代替，在对象的最后比较时要用“小中取大”原则，即对评价对象按总评价指标的得分大小排序[9].

2 自然灾害风险等级评价指标体系与评价原则的建立

针对突发自然灾害，考虑应急物流的时效性，建立评价的指标体系[1]，见图1.基于前述突发自然灾害受灾程度评价指标构建的原则，并按照突变级数法，将突发自然灾害受灾程度评价指标体系设计为由下层指标向上层综合，最后化为0－1的数，即突变级数，将突变级数由大到小排序，排列在前面的地区便是受灾最为严重的地区，具体指标突变如图1所示.

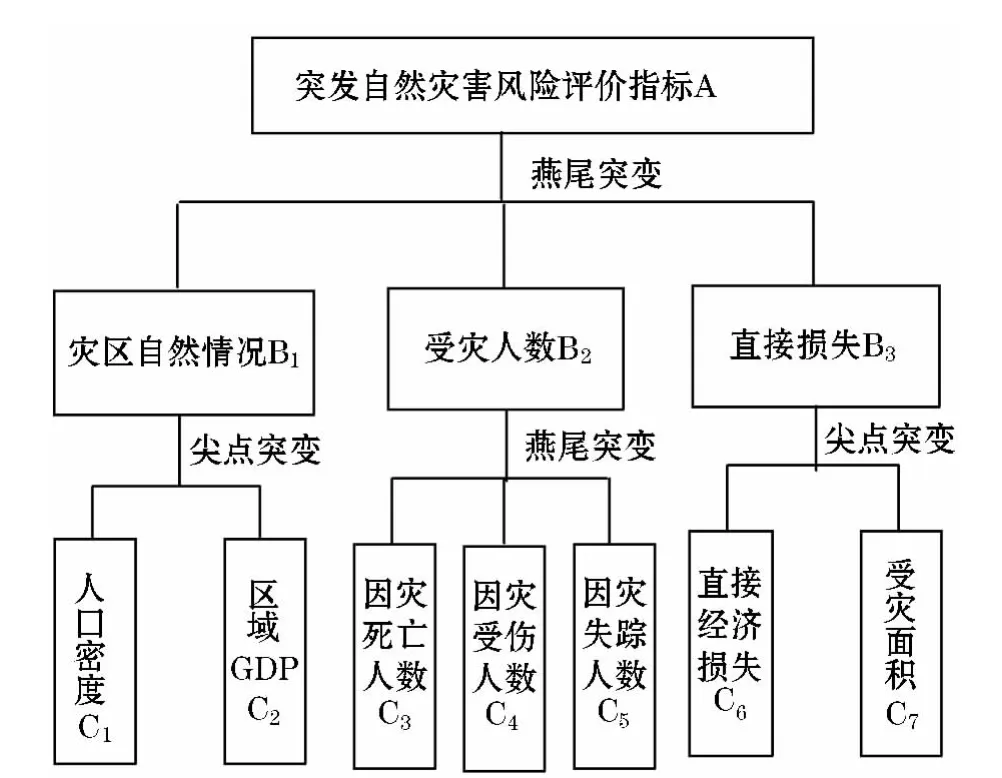
图1 突发自然灾害风险等级评价指标突变系统

3 评价过程及结果

3.1 数据选取

近几年中，发生在我国的突发自然灾害的案例中，地震是常见且又危害最大的一种，而地震带来的损害可以说是巨大的.可以说2008年汶川地震是我国近年来发生的地震最为严重的典型，并且给四川省带来了严重的损失，破坏程度亦属罕见.因此本文选取汶川地震作为例子进行实证研究.

选取的样本数据如表1所示.

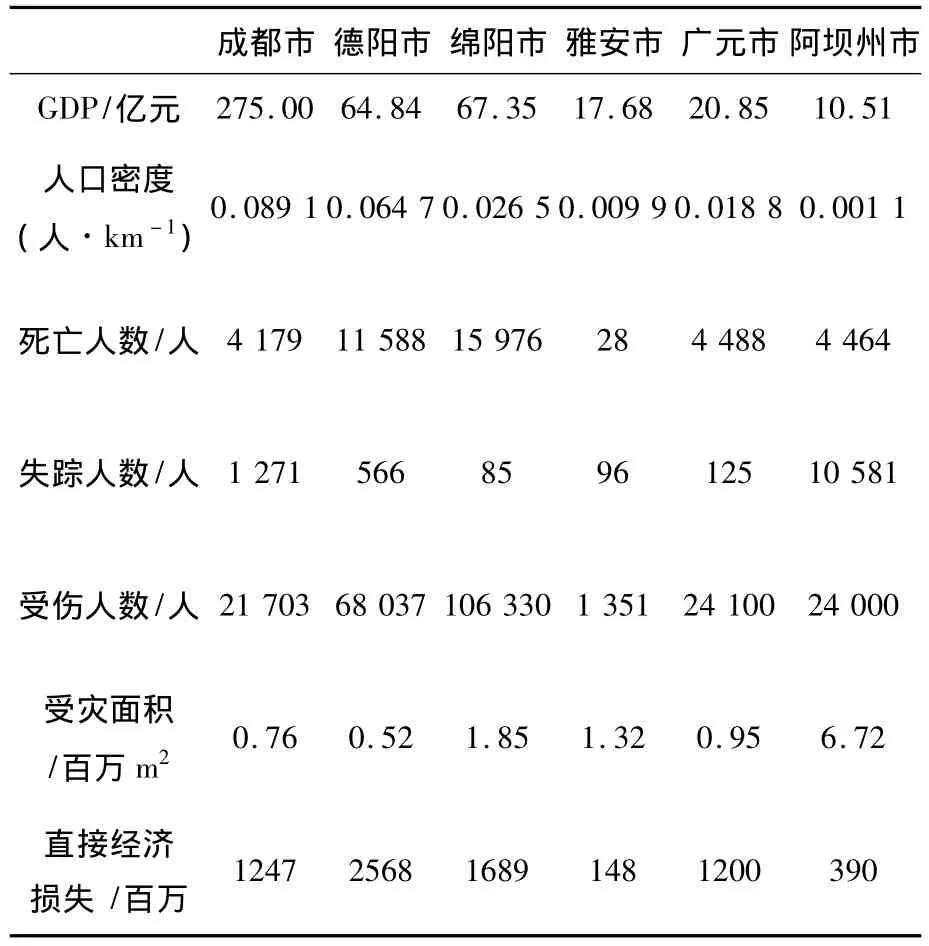
表1 汶川地震造成损失的部分地区的数据

运用数据归一化公式将数据变为[0，1]的值，归一化公式如下:

其中:x∈[xmin，xmax]，xmin，xmax分别为最小值与最大值.结果见表2.

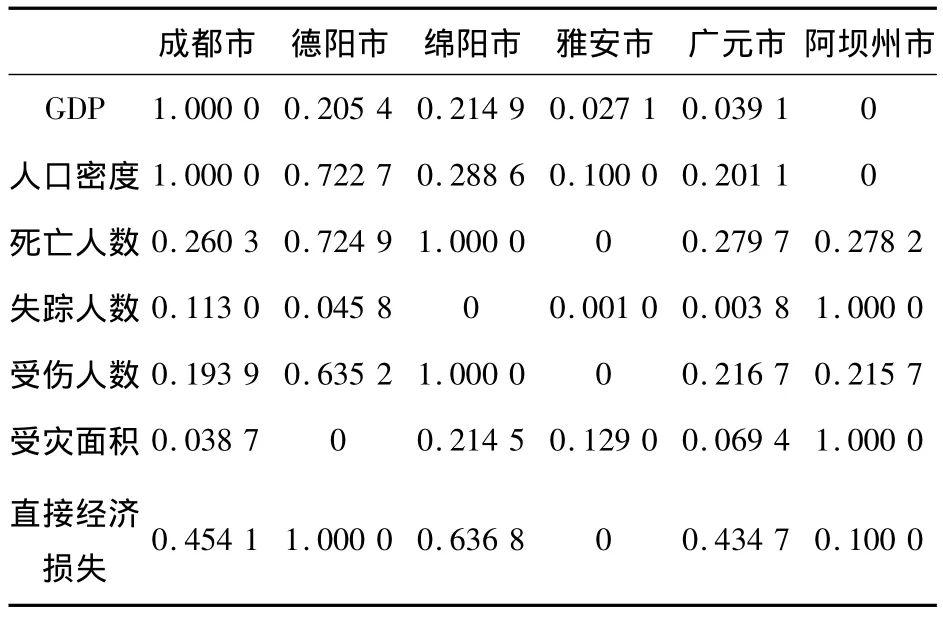
表2 原始数据的归一化结果

3.2 突变级数法的评价结果

3.2.1 指标排序和指标之间的相关性

采用因子分析分析各层指标的重要性和指标之间的相关性，确定每层指标的优先级顺序和第一层与第二层指标系统的非互补或互补类型.为了分析的准确性，本文采用归一化前的数据做分析.

以第三层的第二个突变系统受灾人数系统为例，公共因子一对应的死亡人数、失踪人数、和受伤人数的系数分别是0.979、－0.399 和 0.984(见表3、4)，所以系统指标的优先顺序为受伤人数(C5)、死亡人数(C3)和失踪人数(C4).同时，通过相关性的KMO检验，在显著性水平为0.05下，检验的p值为0.002，小于 0.05(见表5).因此，说明这三个指标变量是相关的，说明此突变系统属于互补型的.同理，可以确定第一个突变系统属于互补型的，指标优先级顺序为GDP(C1)、人口密度(C2.)第三个突变系统属于非互补型的，指标优先级顺序为直接经济损失(C7)、受灾面积(C6).

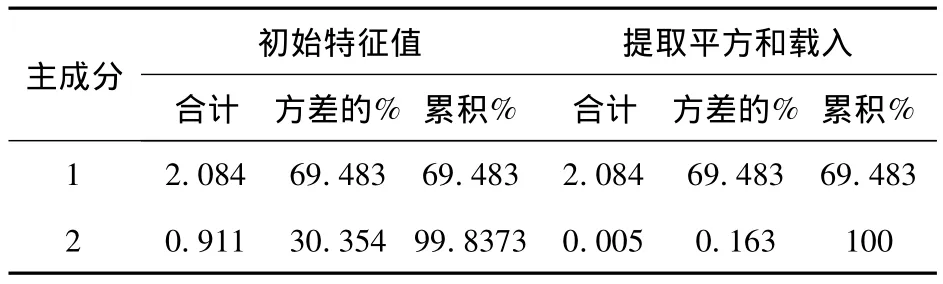
表3 解释的总方差

表4 主成分得分矩阵

表5 KMO—Bartlett检验结果

3.2.2 计算突变值

应用突变级数法进行各层指标的计算，过程如下:灾区自然情况包含C1，C2这两个控制变量，构成尖点突变模型，两者之间属于互补关系，按互补原则取其均值作为上一层指标值，即:B1=(C1/21+

受灾人数情况包含C3，C4，C5三个控制变量，构成燕尾突变模型，三者之间的关系，属于非互补关系，按取小原则，即:B2=(C1/25+C1/33+C1/44)/3;

直接损失情况包含C6，C7两个控制变量，构成尖点突变模型，属于非互补关系，按取小原则，即:

A总指标包括 B1，B2，B3这三个控制变量，构成燕尾突变模型，属于互补关系，按互补原则取其均值，即A=(B1/21+B1/32+B1/43)/3.

通过计算可得B1，B2，B3和A的值，其结果见表6.

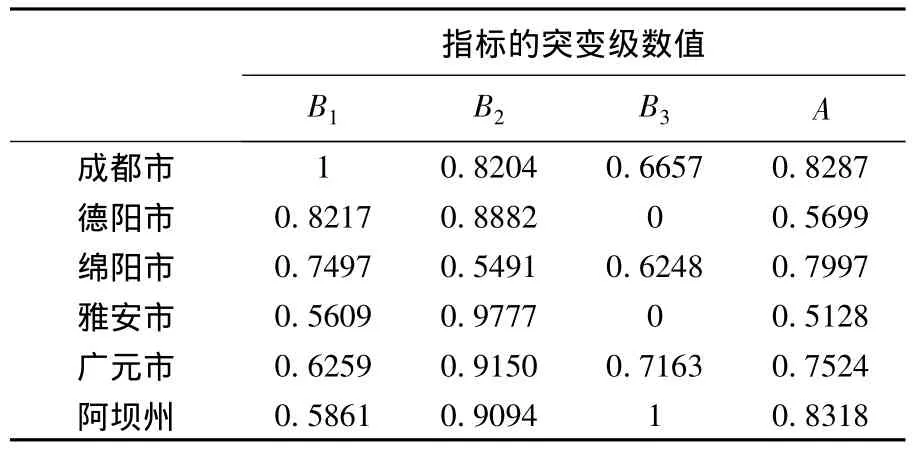
表6 突变级数法计算结果

由表6得到汶川地震影响的6个地区的受灾程度的综合指标值，利用文献[9]中对于灾害风险等级的划分方法，确定本例中每个地区受灾程度等级如表7所示.

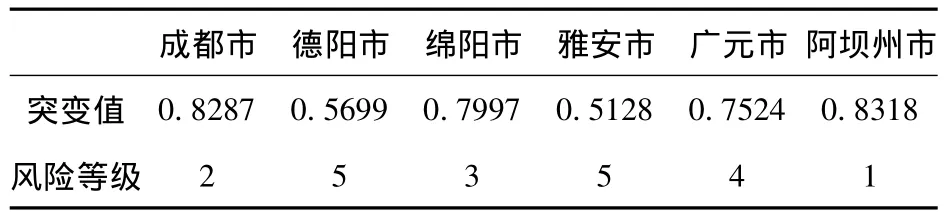
表7 汶川地震影响的部分地区受灾等级

通过以上分析，汶川地震影响的四川省6个地区中，总体来看，阿坝州市和成都市的受灾情况最严重，其次是广元和绵阳市，雅安市受灾程度较轻，并且综合指标值均大于0.5，说明6个地区受灾均严重，也符合了当时受灾的实际情况.国家在此灾难发生时，是启用5级风险预案救援的.从而，说明了突变级数法在突发自然灾害的风险评级中是有效可行的.

4 结语

本文基于突变级数法建立了突发自然灾害风险评级的指标体系，并以汶川地震影响的四川地区为例进行受灾风险等级评价.综上研究，突变级数法在突发自然灾害风险等级评价中，具有思路清晰，计算简单方便的优点，有利于救灾工作的及时开展;同时，不需要采用权重，因而避免了评价的主观性，更符合突发自然灾害具有客观评价的特点.

[1]ZHAO T，FAN H M，WANG G L，et al.Evaluation of the degree of sudden natural disasters affected–a case study of typhoon“Bilis”[J].Energy Procedia，2012(16):1424 －1432.

[2]GREENING L，STEPHEN J D.Adolescents＇perceived risk and personal experience with natural disasters:An evaluation of cognitive heuristics[J].Energy Procedia，1996(91):27 －38.

[3]LI Q G，KANG L，TANG D Q，et al.Applications on spatial information technology in natural disasters[J].Procedia Environmental Sciences，2011(10):1396 －1400.

[4]TSAI C H，CHEN C W.The establishment of a rapid natural disaster risk assessment model for the tourism industry[J].Tourism Management，2011(32):158 －171.

[5]MAGONE E.An analysis for estimating the short－term effects of Japan＇s triple disaster on progress in materials science [J].Energy Procedia，2012(16):289 －297.

[6]ZHANG J.Risk assessment of drought disaster in the maize －growing region of Songliao Plain，China[J].Agriculture，Ecosystem ＆ Environment，2004(102):133－153.

[7]朱顺泉.基于突变级数法的上市公司绩效综合评价研究[J].系统工程理论与实践，2002(2):90－94.

[8]陈晓红，彭 佳，吴小瑾.基于突变级数法的中小企业成长性评价模型研究[J].财经研究，2004(11):5－15

[9]唐桂娟.城市自然灾害应急能力综合评价研究[D].哈尔滨:哈尔滨工业大学，2011.