基于可视化方法的点堆动力学方程刚性分析

余 涛，栾秀春，刘 磊，刘少有

(哈尔滨工程大学核科学与技术学院，哈尔滨150001)

在反应堆动态过程中，空间效应不是主要的，如果我们需要研究中子密度随时间的变化，此时可以应用点堆模型[1].对应于点堆模型下描述反应堆中子密度及先驱核浓度变化的微分方程组称为点堆动力学方程.由于点堆模型的简便，目前已经广泛应用于工程设计中，主要是空间效应不太重要时，比如反应堆、蒸汽发生器的安全事故分析.

在工程设计中需要求解点堆动力学方程，但由于物理过程中的实际情况，求解时会遇到微分方程的刚性问题，给求解带来一定的困难，因此选择合适的求解方法克服方程的刚性显得尤为重要[2－5].利用可视化的方法能够较为直观地表现出动力学的刚性性质，方便对刚性的理解.本文将利用可视化方法，形象地说明点堆动力学方程刚性问题的形成及来源.

1 点堆动力学方程

考虑缓发中子效应后的反应堆动态方程通常称为点对模型动态方程，即点堆动力学方程.

不考虑中子源，缓发中子群数为6时的点堆动力学方程为:

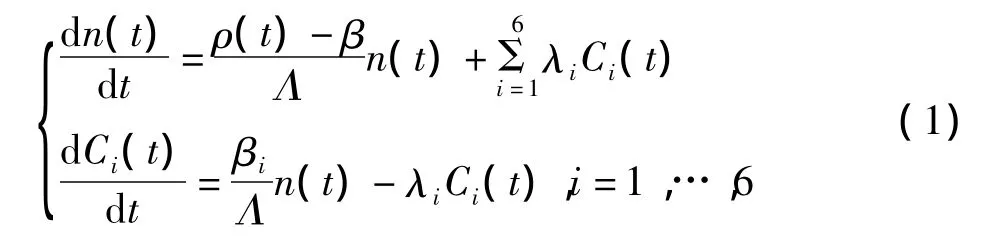
其中:n(t)为t时刻的中子密度;Ci(t)为t时刻第i组缓发中子先驱核浓度;ρ(t)为t时刻的反应性;Λ为中子一代时间即瞬发中子的平均寿命;λi为第i组缓发中子先驱核衰变常数;βi为第i组缓发中子份额

在实际问题中，反应性时时间的函数，如果考虑到功率和温度对反应性的反馈作用，ρ还是中子通量密度或n(t)的函数，因此上述方程一般来讲是非线性的.本文主要探究方程的刚性问题，对方程进行一定的简化，变成一般的线性方程组.

2 方程的求解

上述方程的求解属于微分方程组的初值问题，对于一阶线性常系数微分方程组可以利用函数法求解，假定其解具有以下形式:

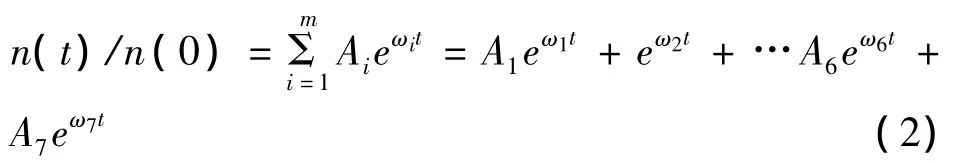
和

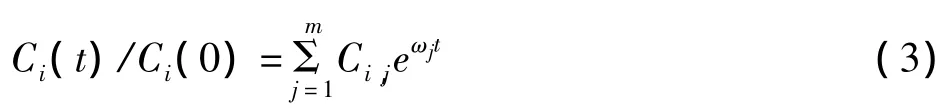
式(2)(3)中 ωi为特征参数，Ai、Ci，j为系数.

3 方程的刚性分析

3.1 刚性系统

在工程中，对于一类过程的可以归结为一般常微分方程的初值问题[6]:

1)J的所有特征值的实部Reωi＜0

则称方程(1)为刚性方程组，r为刚性比.根据Shempine和Gear的观点，如果矩阵J的所有特征值ωi的实部都不是很大的正数，同时至少有一个特征值是很大的负数，则该系统也视为具有刚性的.

3.2 点堆方程的刚性

考虑在热堆中输入正阶跃反应性的过程，Λ=0.000 5 s，βi:0.000 285、0.001 598、0.00 141、0.003 052、0.000 96、0.000 195;λi:0.012 7、0.031 7、0.105、0.311、1.4、3.87;输入的正阶跃反应性:ρ=0.001，计算时间为 100 s.

根据图解法可求得:ωi:0.018 2、－0.013 6、－0.059 8、－0.183、－1.005、－2.875、－55.6，设定ω1＜ ω2＜ …… ＜ ω7，f(i)=Aieωit(i=1，2，…，7).在t=0 s时，反应堆中输入阶跃反应性，fi随时间增加，图1中f(1)从t=0 s时刻反应性输入后持续增加，以指数形式增大，变化趋势较为明显;f2、f3、f4、f5、f6等 5 条曲线变化趋势几乎一致，在图中部分曲线近乎重合，同时图中基本看不出这几条曲线的变化趋势，近乎为一条直线;f7曲线在t=0 s时刻后有一个增大过程，但图1中无法分辨变化幅度与变化变化时间.图2为f1～f7在不同坐标系下的变化曲线，图中明显可以看出f1的值比其他几项大，所以造成了图1中f2～f7的幅值变化无法清楚地显示.

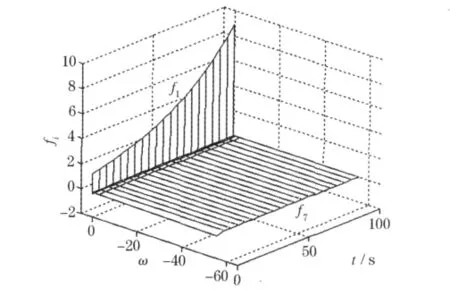
图1 反应性正阶跃输入时0～100 s内中子密度变化

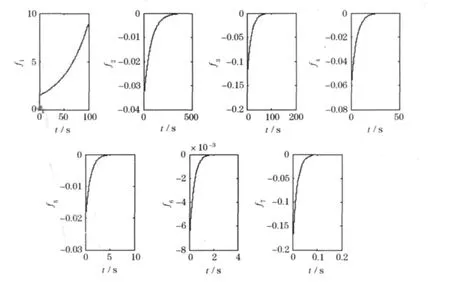
图2 f1～f7在不同坐标系下的变化曲线

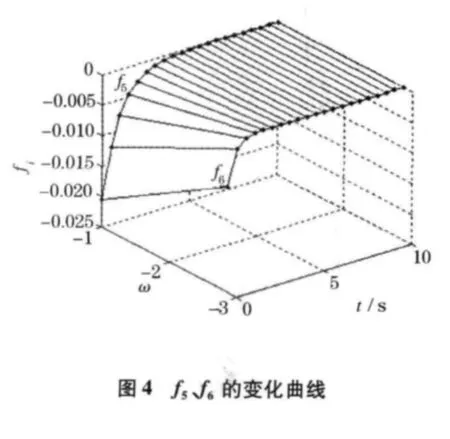
图3、4 分别为f2、f3、f4和f5、f6的变化.对比图3、4中各项与图1中各对应项，图3较为清楚地展现了各项的变化规律，f2、f3、f4项在100 s内持续明显的增大.在图2中，延长计算时间后发现，f1持续增大，f2在t=450 s后趋于0，f3在t=100 s后趋于0，f4在t=30 s后趋于0;图4中可以看出f5、f6在反应性输入后一段时间内增大，然后趋于0，趋于0的时间点分别为:5、2 s，而在图1中则无法看出.

图5为f7在0～1s内变化曲线，在0～0.5 s内，该项由－0.179变化到0左右，0.1 s之后则基本为0，变化趋势与f2～f6相同.由于该项的增长时间较短，因此在图1中无法分辨出增长时间段长度.从上述计算结果图示可以看出，式(2)中右边各项在反应性输入后均随时间增加，第1项持续明显增加，没有趋于一个稳定值，其余6项也随时间增加，但在结果一段时间后趋于稳定值零，各项趋于稳定值的时间依次减小.对于图1中的曲线，由于各曲线对时间的响应速度不一致，图中无法清楚显示各项的变化，因此需要在不同图示中显示各项的变化，这正是方程组刚性性质存在所造成的.

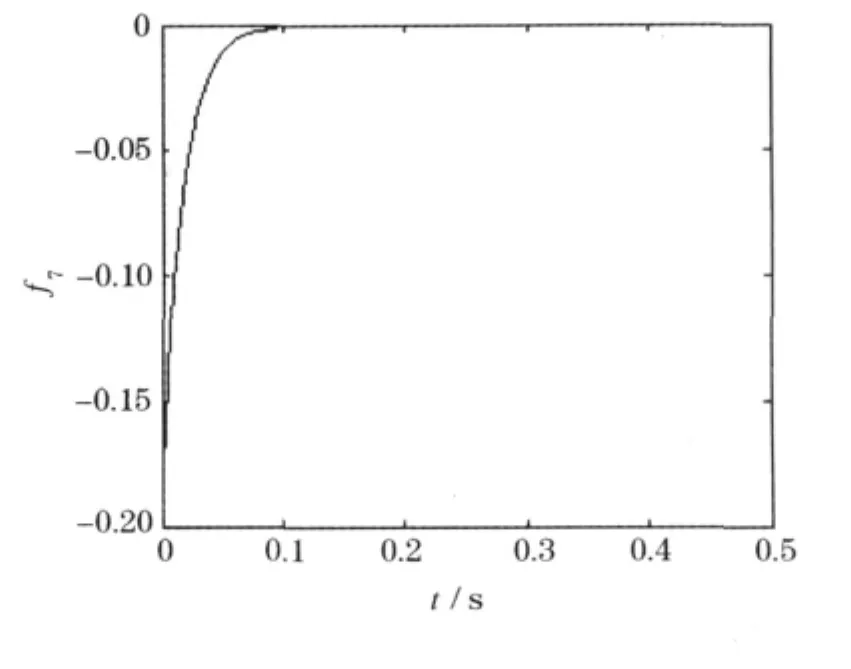
图5 f7的变化曲线

对于正阶跃反应性输入时，式(2)中:A1＞0，ω1＞0;Ai＜0，ωi＜0(i=2，…7)，从而造成上述f1变化趋势与其他各项不同的现象，在f2～f7曲线中，由于各Ai、ωi之间数量级的差异较大使得图1中显示的曲线近乎重合.图5中，f7的变化时间为0 ～0.1s，在 0.1s内，f7有一个较大的增大过程，在相同时间段内，f1～f6的变化量较小，说明在0～0.1s时间段内，中子密度的变化主要是由f7贡献的，而在0.1s后，f7趋于零.图1中显示的则是在0s时刻的一个阶跃，即曲线斜率趋于+∞，说明在一个比较大的时间尺度下，f7无法正常体现出来.对应于在式(1)的数值求解过程中，如果选取的时间步长过大，则对于方程的稳定性无法保证，因此由于f7的存在需要在数值求解时选取较小的时间步长，保证计算方法的稳定性以及计算结果的正确性.但是如果选择较小的计算步长，则对计算效率和计算时间产生影响.由于f7对中子密度时间响应的贡献只存在于0.1 s内，0.1 s后基本不需要考虑f7的影响，也就不需要采用因该项而决定的时间步长，从而造成计算效率的浪费.过小的计算时间步长在进行较长计算时间的计算时意味着较长的工时.在工程设计中，上述选择计算时间步长限制的矛盾正是系统刚性性质的表现.

由于刚性微分方程的求解特殊性，因此在工程设计中尽量避免刚性微分方程，但由于实际过程的限制，实际过程中的多数方程都具有一定的刚性，其中一些的刚性还较大.对于式(1)，根据刚性系统的定义，在 ρ=0.001阶跃输入时，方程符合Shempine和Gear对于刚性系统的观点;在ρ=－0.001阶跃输入时，方程刚性比r为1 000，符合刚性系统的定义.在刚性系统的定义中，判断是否是刚性系统取决于特征值 ω，对于点堆方程由下式[7]:

ω1＞ －λ1＞ω2＞… ＞ω6＞ －λ6＞ω7＞l－1(5)其中:l为中子寿命，根据式(5)可知，由于反应堆缓发中子先驱核衰变常数的限制使得方程(1)的各个特征值ωi之间相差较大，对于热堆，λ1大约为10－2数量级，λ6为 101数量级，l－1为 103数量级，因此在负阶跃反应性输入时，ωi＜0，此时方程刚性比为102～104数量级，属于刚性系统.

4 结语

在可视化方法的基础上，分析了点堆动力学方程的刚性性质，方程刚性是由核反应堆的物理性质决定的，即堆内缓发中子先驱核的衰变常数以及中子一代时间之间相差数个数量级，从而使方程具有较大的刚性.

[1]谢仲生.核反应堆物理分析[M].西安:西安交通大学出版社，2004.

[2]陈 东.求解点堆中子动力学方程的三角插值法[J].原子能科学技术，2010，44(10):1195 －1200.

[3]胡大璞.克服点堆中子动力学方程刚性的新方法——端点浮动法[J].核动力工程，1993，14(2):122－128.

[4]黎浩峰.用高阶泰勒多项式积分方法求解点堆中子动力学方程[J].原子能科学技术，2008，42(增刊):162－168.

[5]NAHLA A A.Taylor’s series method for solving the nonlinear point kinetics equations[J].Nuclear Engineering and Design，2011，241(5):1592－1595.

[6]黄祖洽.核反应堆动力学基础[M].北京:北京大学出版社，2007.

[7]谢仲生.核反应堆物理数值计算[M].北京:原子能出版社，1997.