分数布朗运动环境下可转换债券定价模型

李琛炜，薛 红

(西安工程大学 理学院，西安710048)

可转换债券是发行公司事先规定持有人有权在债券到期日(或到期前)按发行时规定的转换比率将其持有的债券转换成发行公司的股票.可转换债券是一种新型的金融衍生产品，是一种期权式债券.文献[1]在假定股票价格服从几何布朗运动的条件下，研究了发放红利对可转换债券定价的影响.文献[2]利用随机分析理论和鞅方法，得到了几何布朗运动环境下支付红利的可转换债券定价公式.分数布朗运动具有自相似性、长期相依性等特征，它能很好地刻画标的资产的价格波动规律，这使得它成为研究标的资产价格过程的一个更为合适的工具.关于分数布朗运动随机分析理论可参见文献[3－4].文献[5]在无风险利率、股票价格的期望收益率和波动率均为常数条件下，利用风险中性概率测度，得到了分数布朗运动环境下可转换债券的定价公式.本文在无风险利率r(t)、期望收益率μ(t)、股票波动率σ(t)和红利率1(t)均为时间的确性函数条件下，建立分数布朗运动环境下的金融市场数学模型，利用分数布朗随机分析理论，得到了具有支付红利的可转换债券定价公式，推广了文献[5]的结论.

1 分数布朗运动环境下金融市场数学模型

假设金融市场仅有两种证券，一种是无风险资产即债券，其价格满足方程

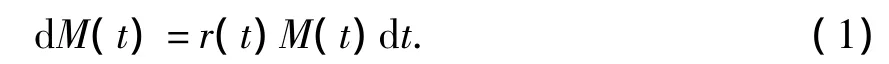
其中:r(t)为无风险利率，另一种风险资产即股票，其价格满足

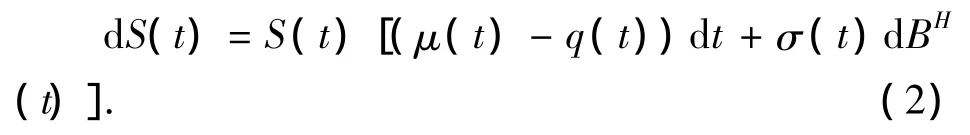
其中{BH(t)，t≥0}是定义在完全概率空间(Ω，F，P)上的分数布朗运动，μ(t)为期望收益率、q(t)为红利率、σ(t)为股票波动率，引入新的等价概率测度Q，满足

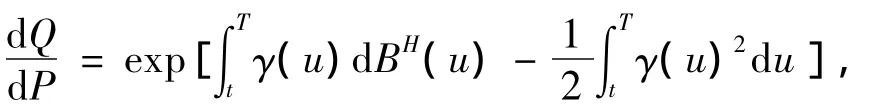
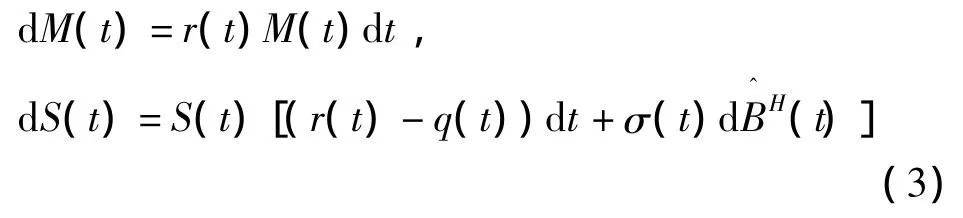
引理1[6](分数风险中性定价)任意自然σ流上的可测未定权益ζ在任意时刻t∈[0，T]的价格为其中[·]为概率测度下的拟条件数学期望.

引理2[6]设函数f满足E[f(BH(T))]＜∞，则对任意t≤T有

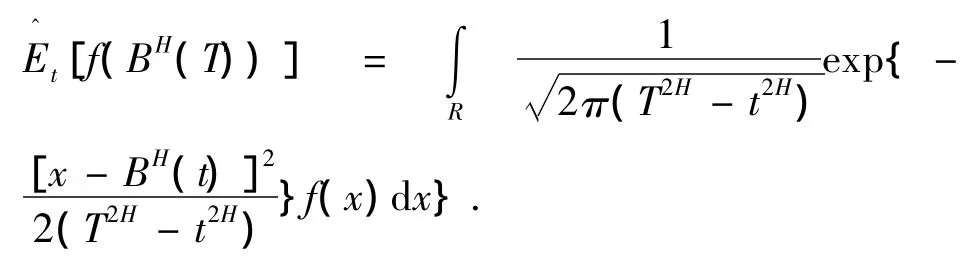
定理3[6]随机微分方程(3)的解为

且

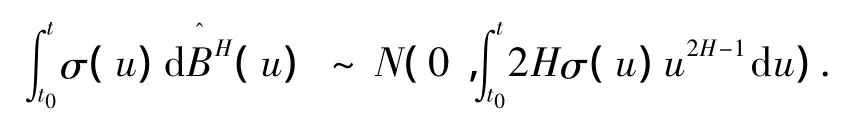
2 分数布朗运动环境下支付红利的可转换债券定价

定义4[5]假定可转换债券的转换只可发生在债券到期时刻T，可转换债券时刻T的价值VT为

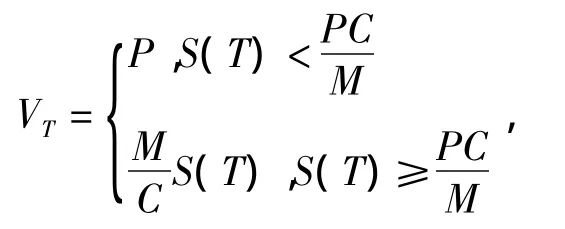
其中:P代表单纯的债券价值，C代表转换价格，M代表债券的面值，S(T)代表时刻股票价格.

定理5可转换债券在t时刻价值为

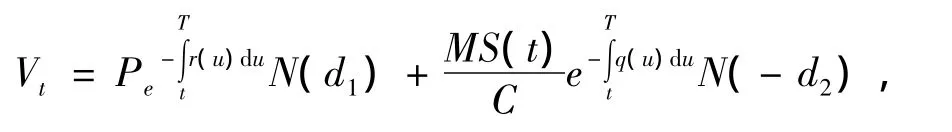
其中

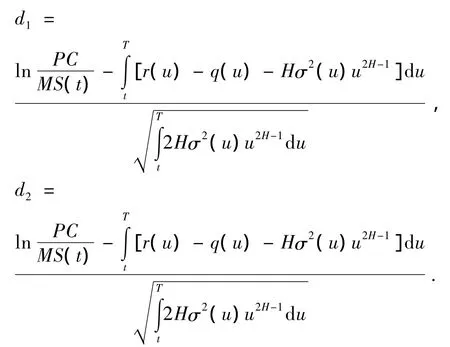
证明 可转换债券在t时刻价值

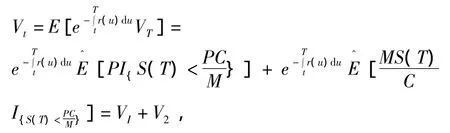
其中

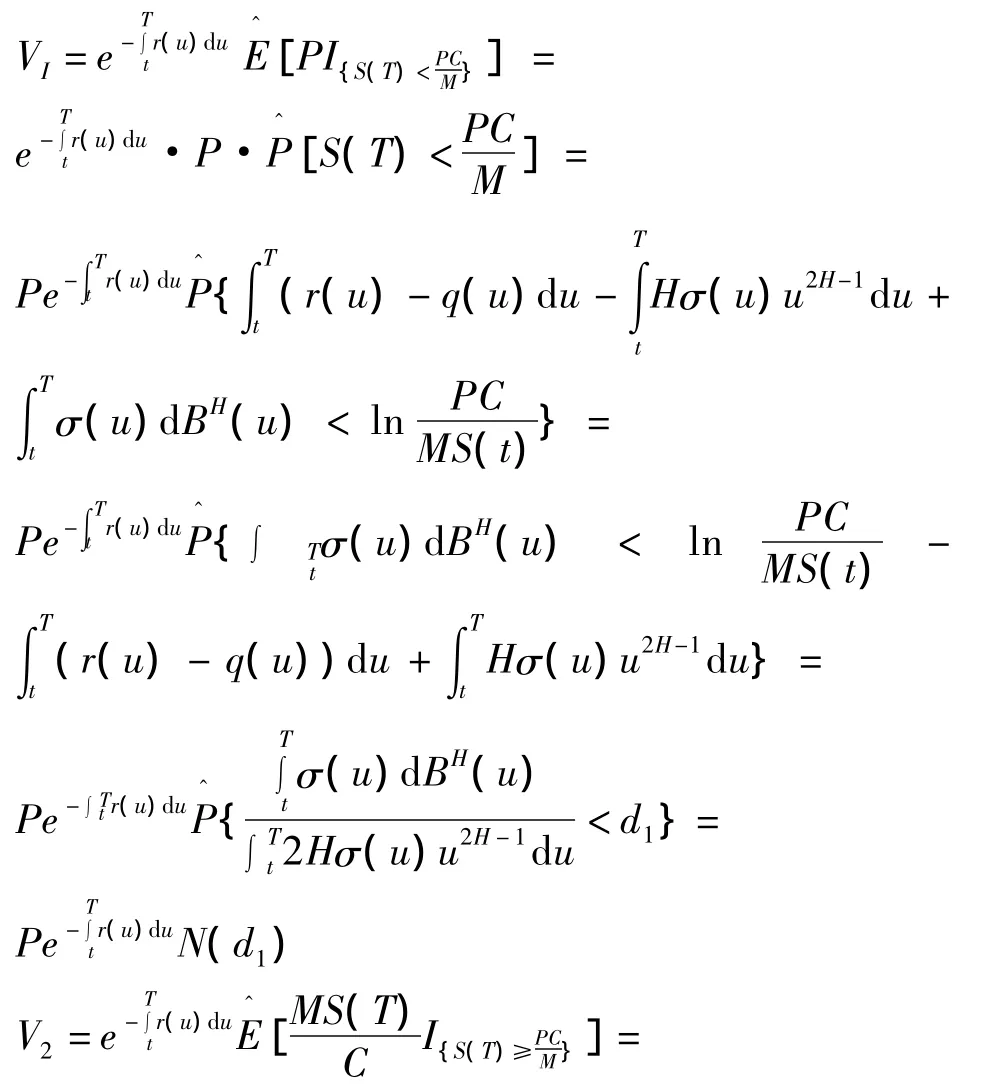
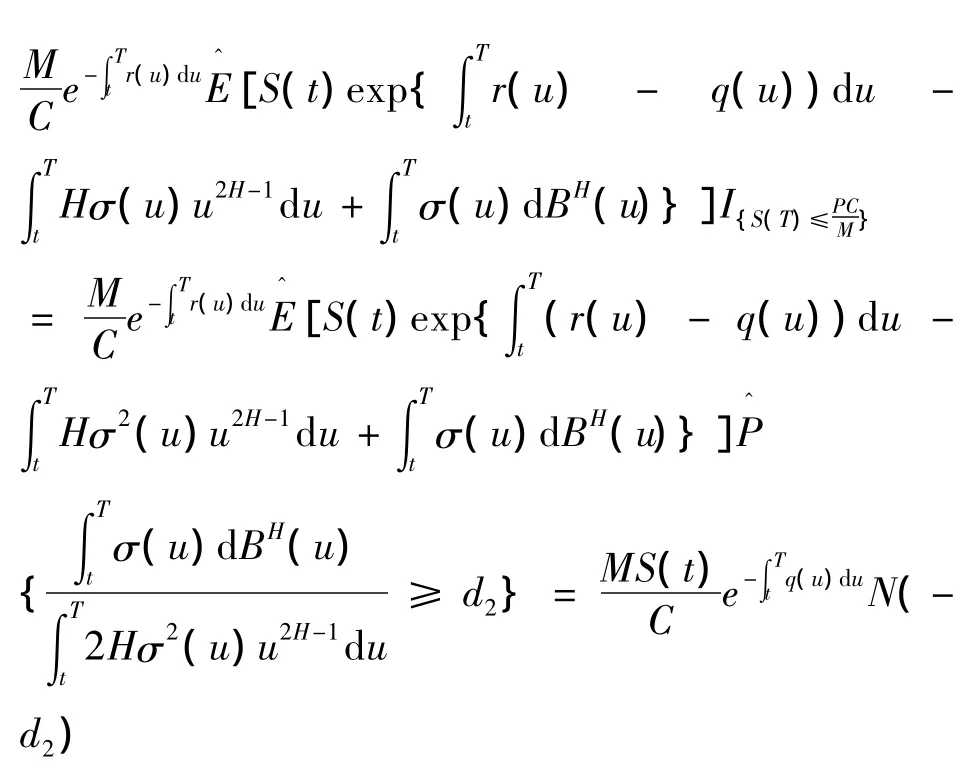
注 当t=0，无风险利率、期望收益率和波动率均为常数且不考虑分红时，可得文献[5]结果

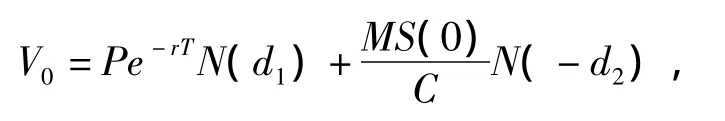
其中:N(x)为标准正态分布的分布函数，且

特别地，当t=0，无风险利率、期望收益率和波动率均为常数且不考虑分红时，可得文献[7－8]结果，

其中N(x)为标准正态分布的分布函数，且

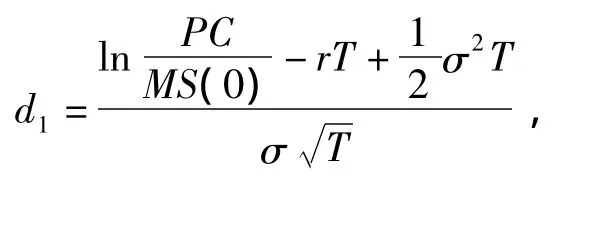
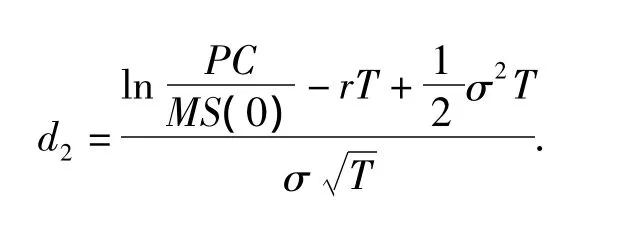
3 结语

本文借助分数布朗运动随机分析理论，建立了分数布朗运动环境下的金融市场数学模型，得到了分数布朗运动环境下具有支付红利的可转换债券的定价公式，对可转换债券市场的价格定制具有重要参考意义.

[1]于春红，周 璐.我国可转换债券定价的实证分析[J].商业经济，2007(3):614－618.

[2]于 萍，孔繁亮.鞅分析在周期红利下n－因子可转换债券定价中的应用[J].哈尔滨理工大学学报，2008，13(2):123－127.

[3]GUASONI P.No arbitrage under transaction costs with fractional Brownian motion and beyond[J].Mathematical Finance，2006，16(3):569－582.

[4]BIAGINI F，HU Y，OKSENDAL B，et al.Stochastic calculus for fractional Brownian notion and applications[M].New York:Springer，2008.

[5]沈明轩.分数布朗运动环境中可转换债券的定价[J].安徽工程科技学院学报，2010，25(4):72－74.

[6]刘韶跃.数学金融学的分数型Black－Scholes模型及应用[D].长沙:湖南师范大学，2004.

[7]王振全，邓述慧.简单可转换债券的定价—一种鞅方法[J].经济数学，2010，17(4):1－8.

[8]蔺 捷，薛 红，王晓东.分数布朗运动环境下缺口期权定价模型[J].哈尔滨商业大学学报:自然科学版，2012，28(5):616－619.