滑动式测斜仪测试与误差处理方法

李国维，胡龙生，王 润，陈达章

(1.河海大学土力学与堤坝工程教育部重点实验室，江苏 南京 210098;2.河海大学道路与铁道工程科学研究所，江苏 南京 210098;3.河海大学岩土工程科学研究所，江苏 南京 210098;4.国家知识产权局专利局专利审查协作江苏中心，江苏 苏州 215000;5.广东省广乐高速公路有限公司，广东 清远 511500)

近年来高速铁路、公路和水利工程项目众多，建设期及运行期的安全问题受到格外重视［1］。

测斜仪是一种监测岩土体水平位移的原位监测仪器，可用于观测各类工程不同深度的岩土体水平位移［2］。边坡工程可通过深层水平位移曲线判定滑动面位置及滑移方向和数量;软基工程土体的侧向水平位移是评价地基处理效果的重要指标［3-6］;深基坑工程墙壁土体的水平位移过大会危及周边建筑物的安全［7］。西方国家自20世纪60年代开始大量使用测斜仪;而我国在引进国外测斜仪的基础上，随着材料、传感器、集成电路、计算机等高新技术的发展，至20世纪90年代，测斜仪测试技术应用研究也取得了显著进展［8］。

滑动式测斜仪在监测过程中受到多方面因素的影响，存在各种误差。位移累加后，误差累积效应明显，影响了测斜仪测试精度，不能真实反映土体位移。对于深孔测斜仪测试技术，因环境变化大，测试时间长，存在测试过程中的零点漂移问题，误差修正问题尤显重要。

有关学者对测斜仪的误差问题进行了研究。王虎子［9］对由于测斜仪电缆伸长而引起的对位误差进行了理论分析，并研制出无伸长电缆;靳晓光等［10］提出钻孔测斜仪量测数据评价和处理方法，给出了量测深度修正公式;考虑到地震、爆破、支护施工等因素对测斜仪测试过程的影响，吴逸等［11］提出了利用小波减噪法对监测数据进行减噪。针对测斜仪测试数据处理过程出现的测距、正反两测次读数差值等问题，叶锋等［12-14］进行了大量研究，并提出了修正方法。然而避免各类误差的相应系统测试技术还少有文献论述，尤其针对零点漂移误差，尚未有方便的消除方法。

笔者研究发现:部分测斜仪测试数据出现明显零点漂移问题，会导致深层位移方向与实际位移方向相反，位移量偏大或偏小。本文在现场测斜经验的基础上，结合现场测斜仪测试数据，分析了测斜误差来源，并对控制各类误差的测斜技术及零点漂移误差修正方法进行了探讨。

1 滑动式测斜仪

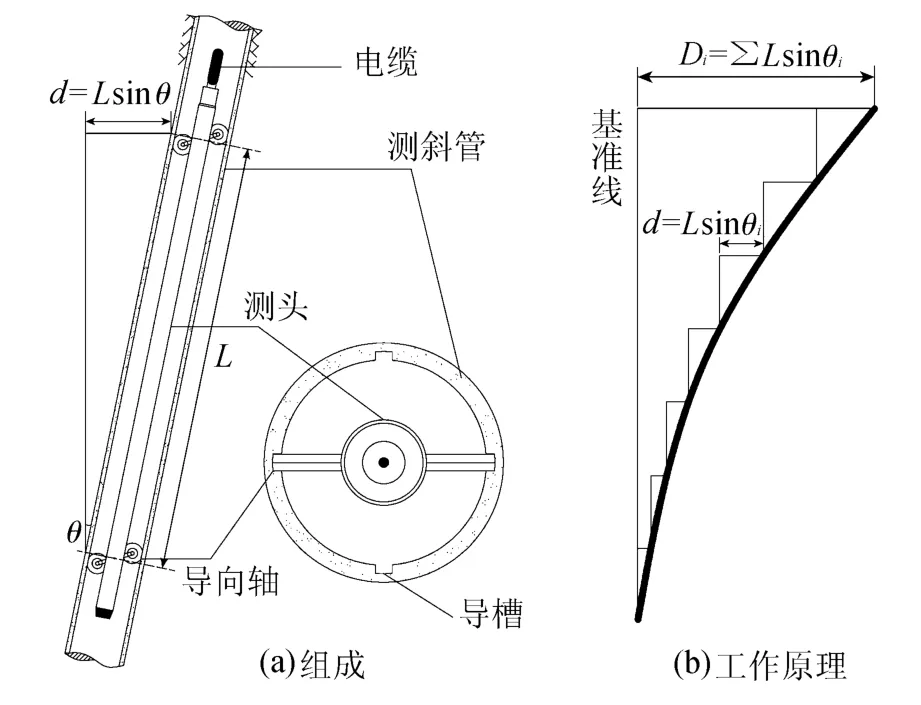
图1 滑动式测斜仪主要组成与工作原理示意图Fig.1 Main composition and operating principles of a skip inclinometer

测斜仪是一种高精度角度测量仪器，按照使用方式可分为滑动式测斜仪和固定式测斜仪。固定式测斜仪造价昂贵、测点稀疏，工程监测中一般多应用于地理环境复杂、现场条件恶劣的高陡边坡。而滑动式测斜仪测点密集、成本低、方便易行，在工程界应用广泛。

滑动式测斜仪由测头、读数仪、电缆和测斜管四部分构成。工作原理是:传感探头逐段测量测斜管轴线与基准线的夹角，由三角函数关系可计算出每测段测斜管上下轮所在位置在某一方向发生的相对位移量，逐段累加后求得测斜管在不同深度的绝对位移量［15-16］，见图1。

某一测点所发生的位移为

式中:L——测距，通常为50 cm;θi——某测段测斜管与基准线夹角。

根据文献［17］，测斜管埋设时设计深度应超过最深位移带5 m，深入稳定基岩内。测斜管管底视为不动点，故土体在不同深度发生的绝对位移通过逐段叠加的方式求得

2 测斜仪测试误差种类

测斜仪的位移最小精度能达到0.01 mm［18］。受仪器本身、人为因素和现场环境影响，测斜仪测试误差主要包括系统误差、人为误差、环境误差三类。

系统误差主要包括:零点偏置误差、零点漂移误差和旋转误差、测斜管在制造和安装过程中可能发生扭曲而产生的扭曲误差;人为误差主要是指测斜仪在测量过程中操作不当产生的误差;环境误差是指测斜仪受环境温度和湿度的影响产生的误差。三类误差之间相互影响，如环境改变(温度)和人为操作不当均会影响系统误差，故测斜仪测试误差是各种因素的综合体现。

3 误差控制

3.1 系统误差控制

测斜仪系统误差来源主要有三部分，分别为测头(探头)、读数(仪)系统、测斜管。测头本身存在零点偏置误差，在使用过程中受机械震动和环境变化的影响，易产生零点漂移误差，零点漂移误差较大时需要修正。读数系统正常工作需要一定的电压区间，测量前需确保读数仪电量充足。测斜管在安装过程中需技术人员指导，在下放过程中要实时调整导槽方向，防止测斜管发生扭曲而产生扭曲误差。

3.2 人为误差控制

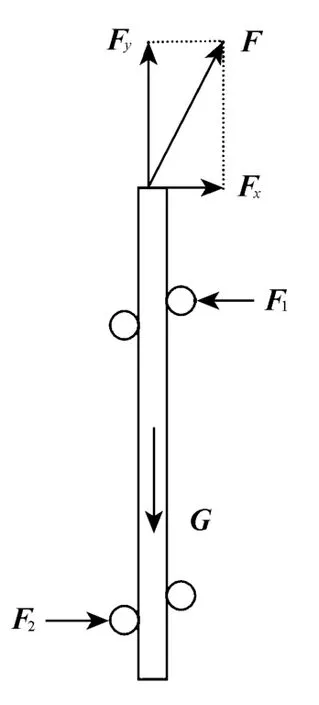
图2 测斜仪(拉测方向与量测方向一致)探头受力示意图Fig.2 Force diagram of inclinometer probe when pulling and measuring in same direction

人为误差是指测斜工作者经验不足和不良测量习惯而产生的误差，其主要来源于正反两次测量时探头相对位置不一致、拉测方向不相同以及数据记录时读数仪不稳定。为了防止正反两次测量对位不一，测斜仪测试过程中应选择电缆标签的同一点作为参考点与测斜孔孔口对齐并拉紧，必要时可于测斜管管口做相应的标记。理论上，拉测方向应与测斜管轴向保持一致。但由于测斜仪测试过程中存在定点问题，实测时难以达到要求。

若选择和量测方向一致的两孔口导槽作为拉测方向控制点，测头受力示意见图2。测拉力F与测斜管轴线存在一定夹角，F分解为水平分力Fx和竖直分力Fy，Fy与测头自重G平衡，Fx等效于在量测方向施加了微小弯矩，测头在量测方向发生偏转，从而影响测斜仪测试数据的精确度;同理，若选择与量测方向垂直的孔口导槽作为拉测方向控制点，拉测方向测斜仪测试数据受Fx影响较大，量测方向影响可以忽略。综上，拉测方向应选择图3中1或2。另外读取数据时，需待读数仪稳定后再记录。

3.3 环境误差控制

测斜管底部通常存在地下水，地下水温度常年基本保持恒定，一般为15～17℃。室外气温变化频繁，南方地区气温偏高，夏天气温可达35℃以上。温度骤变对测斜仪精度有较大影响。测试前需将探头放置于测斜管管底，待其温度平衡后再进行观测。现场经验表明:当室外气温不高、温差不大时，需放置5～10min;当室外气温较高，温差较大时，需放置10～15min。

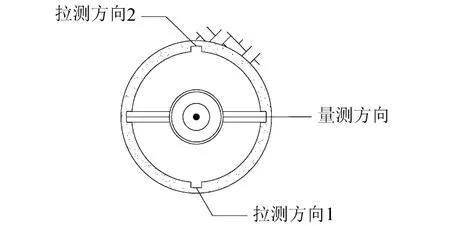
图3 测斜仪拉测方向示意图Fig.3 Schematic diagram of pulling directions of an inclinometer

4 零点漂移误差修正方法

4.1 零点偏置误差

滑动式测斜仪测头在绝对竖直状态下，理论测值应严格为0，但探头在制造和使用过程中受各种因素的影响，实际输出并非为0，这就是零点偏置误差。

测头内部传感元件(以伺服加速度计式为例)，当加速度计敏感轴与铅垂线存在倾角θ时，加速度计输出一个电压信号。正向测量时其输出值为

为了消除K0影响，实际测量时将探头反转180°进行二次观测，即负向测量。负向测量时其输出值为

式中:δ0，δ180——正向测量、负向测量读数;K0——零点偏置误差;c——仪器标定系数。

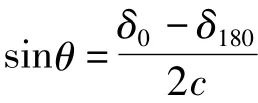
4.2 零点漂移误差

在一次测量过程中，零点偏置误差通常为常数，即K0为恒定值。但探头在使用过程中受环境改变、机械震动等因素的影响，K0往往不为常数，即由于K0变化而产生的误差称为零点漂移误差。

彭立威［19］提出利用经纬仪、全站仪、高精度GPS等外观监测仪观测孔口位移，再用倒三角法来消除零点漂移误差。常规仪器在监测过程中本身存在误差大、操作复杂、受气候条件影响明显等问题，难以真正解决零点漂移问题。本文基于测斜仪基本原理，提出统一基准线修正法UBM(unified baseline correction method)，并应用于工程实际中，很好地解决了零点漂移问题。

4.3 UBM原理

当测斜仪探头出现明显零点漂移问题时，按照传统方法处理数据，易出现位移曲线与实际位移方向相反、位移曲线交叉、位移量值偏大或偏小现象。基于测斜仪基本原理，笔者认为:零点漂移问题可以回归为测斜仪测量基准线发生变化的问题，统一测量基准线可以很好地解决零点漂移问题。当探头处于绝对铅直位置时，读数应为零，UBM通过将测斜仪测试数据相对归零，使测量基准线统一为绝对铅直线。

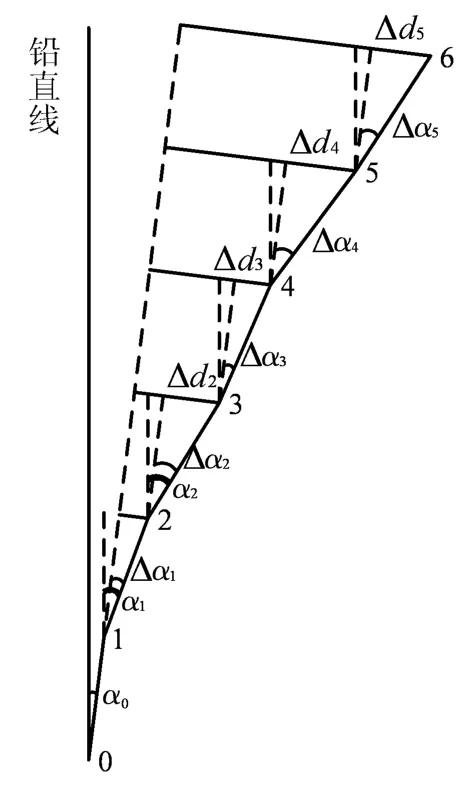
图4 零点漂移恒定误差修正原理Fig.4 Error correction principle when zero shift is constant

4.3.1 零点漂移量恒定

当测斜孔深度不深时，测试过程环境变化小，零点漂移量恒定，测试时间短，测量基准线与绝对铅直线存在一零点漂移角α0，此时土体深层水平位移修正原理见图4。由图4知，零点漂移量大小恒定，统一测量基准线为绝对铅直线，各测点实际倾角应为该测点实测倾角与零点漂移角之差。即

则各测点修正后位移计算公式为

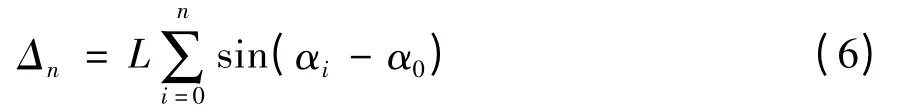
式中:αn——n测点实测倾角;α0——零点漂移角;Δn——n测点修正后绝对位移;Δαn——n测点修正后角度。

式(6)表明:处理实际测斜仪测试数据时，先将各测段读数(包括孔底数据)与实测孔底数据作差值，换算成位移后再通过叠加法计算不同深度的绝对水平位移。故常规方法处理零点漂移测斜仪测试数据时，若α0＞0，易出现位移值偏大的现象;若α0＜0，则会出现位移曲线与位移方向相反或位移偏小的现象;若α0=0，即为理想状态(无零点漂移)。

4.3.2 零点漂移量变化

深孔测斜时，测试过程时间长，环境变化大。由于测试过程中环境变化对零点漂移的影响，即测斜过程中零点漂移量是不断变化的，因此应采用UBM逐段修正。土体深层水平位移修正原理如图5所示。由图5可知，零点漂移量发生变化时，可以用逐段角度作差来实现测量基准线统一为绝对铅直线。

第九，在重视教学质量的同时，不能忽视安全。要切实抓好教学点的安全、稳定工作。对教学点师生经常进行安全教育，开展演练活动，提高安全防范意识及防范技能，要求教学点做好安全应急预案，并督促教学点做好工作台账及安全工作记录，使教学点师生在平安、愉快中工作、学习和生活。

为了分析以曲代直带来的影响，现以图5中A，B，C，D，E 5点为例作矢量运算:

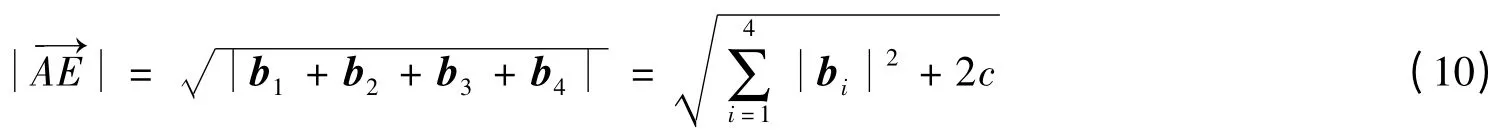
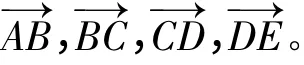
则5点的相对误差为

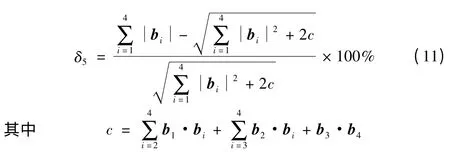
由图中几何关系易得:b1与b2夹角为Δα1;b2与b3夹角为Δα2;b3与b4夹角为Δα3，则b1与b4夹角为∑3i=1Δαi，其他向量之间夹角依次类推。各向量模长为:

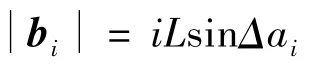
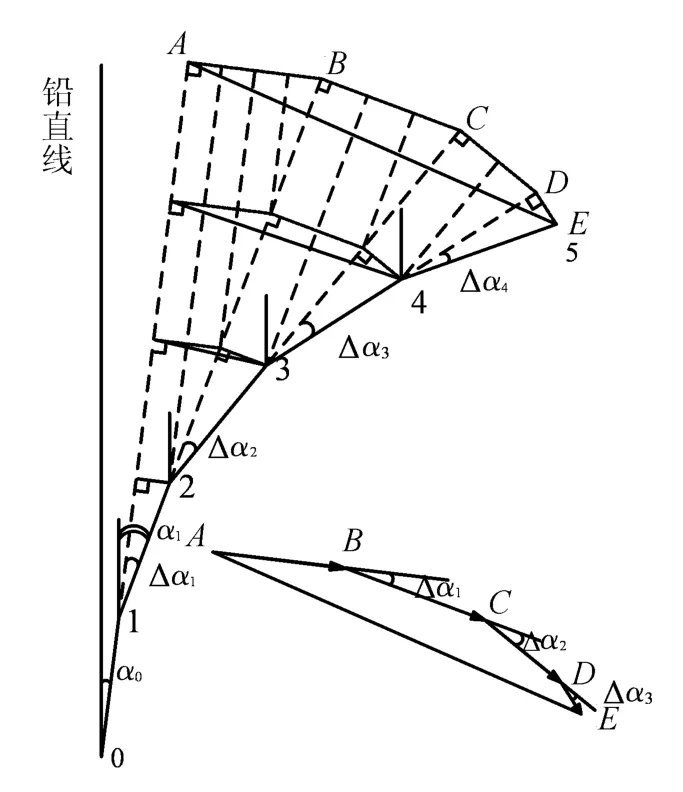
图5 零点漂移误差变化误差修正原理Fig.5 Error correction principle when zero shift is changing

5 工程实例

5.1 概况

为了检验UBM的有效性和适用性，本文以乐昌至广州高速韶关段软基工程、粤赣高速高路堑边坡工程安全监测埋设的典型测斜孔为例，对其实测数据加以处理分析。

RJCX-1测斜孔布设于在建的广乐高速韶关段软基K100+800断面，深度为14.5 m;SLCX-2测斜孔，选择粤赣高速公路某高路堑边坡历史监测资料，孔深为31 m。

5.2 基于UBM消除零点漂移误差

工程实际中，当测斜孔深度低于25 m，可基本忽略测试过程中环境变化对零点漂移的影响，使用4.3.1中的方法修正，即RJCX-1;当测斜孔深度超过25 m时，需考虑测试过程环境变化对零点漂移的影响，采用4.3.2中的方法修正，即SLCX-2。

5.2.1 UBM修正RJCX-1

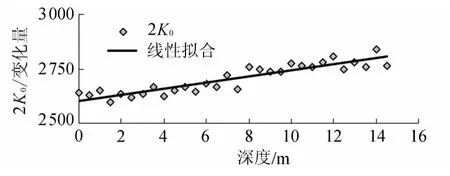
图6 测斜仪测试数据正负向和数(2K0)随深度变化曲线Fig.6 Variation of 2K0with depth for inclinometer

图6为RJCX-1于2012年2月12日实测数据正负向和数(2K0)随测斜孔深度的变化曲线。由图6可知:线性拟合时，数据稍许离散，笔者认为这是测量过程受人为因素及环境因素干扰所致。整体而言，随着测斜孔深度增大，零点偏置误差线性增大，即该测斜仪发生明显零点漂移现象。另外，零点漂移量基本恒定，这也验证了当测斜孔深度不大，可以不考虑环境变化对零点漂移的影响。

软基段路基在填筑过程中，软基处理层发生的位移一般指向路基外侧。由图7(a)RJCX-1修正前曲线可知:2012年1月17日发生负向位移且位移值较大，2012年2月15日位移值明显偏小，且各测次位移曲线发生交叉现象，这均与实际情况不符。由图7(b)可见，修正后曲线与修正前线形基本相似，说明UBM不影响测斜仪线性关系。2012年1月7日位移曲线负向位移基本消除，修正后2012年1月7日与2012年2月15日位移曲线基本重合，即土体未发生位移。实际上该期间施工单位正值春节假期，该路段未进行填土作业，故修正后曲线较好地反馈了土体发生的真实位移。

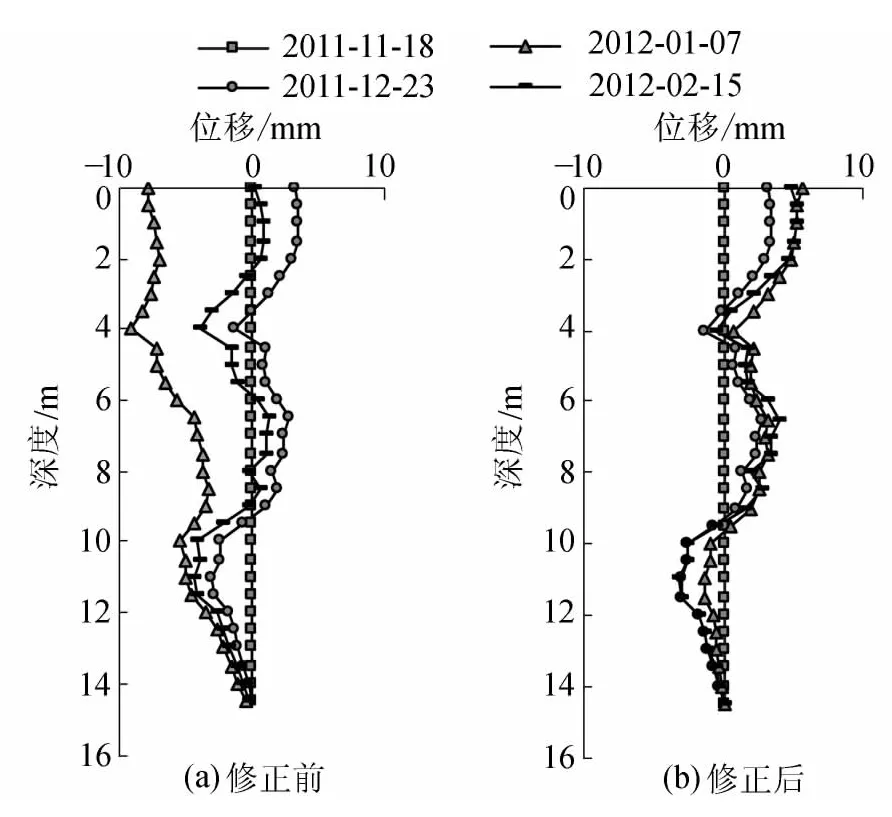
图7 UBM修正RJCX-1前后曲线Fig.7 Correction of RJCX－1 based on UBM

5.2.2 UBM修正SLCX-2及误差评估

图8(a)为SLCX-2修正前位移曲线，图中2005年3月1日、2005年5月27日及2005年7月3日均存在明显交叉现象，这与坡体实际位移变化方向相悖。图8(b)为分别用以曲代直简化修正和精确修正后的位移曲线。修正后，各测次位移大小明显完善，位移曲线交叉现象基本消除。对比修正前后曲线，修正后位移有所增大，这也表明零点漂移误差使位移值偏小。

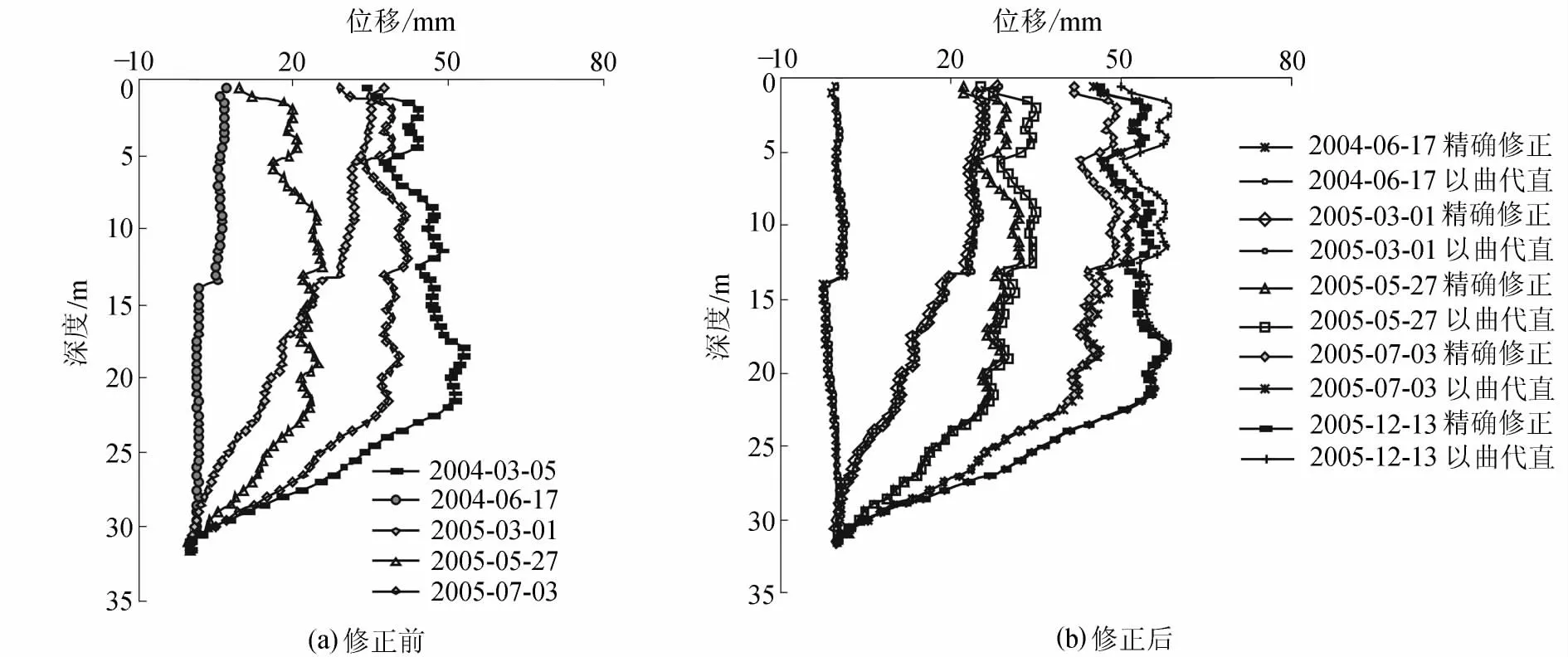
图8 SLCX-2修正前后曲线Fig.8 Curves of SLCX-2 before and after correction

由图8(b)可见，各测次中以曲代直简化修正结果略大于精确修正结果，深部位移曲线基本重合，随着深度的减小，二者差距逐渐放大，这与实际情况相符。

考虑到SLCX-2测斜孔较深，选择0.5 m，5.5 m，10.5 m，15.5m，20.5m，25.5m，30.5m深度对以曲代直简化修正结果和精确修正结果进行对比，结果见表1。以曲代直简化思想引起的相对误差随深度变化曲线见图9。

由表1可见，两种修正结果较为接近，其相对误差在0%～15%之间，以曲代直简化修正结果略大于精确修正结果。

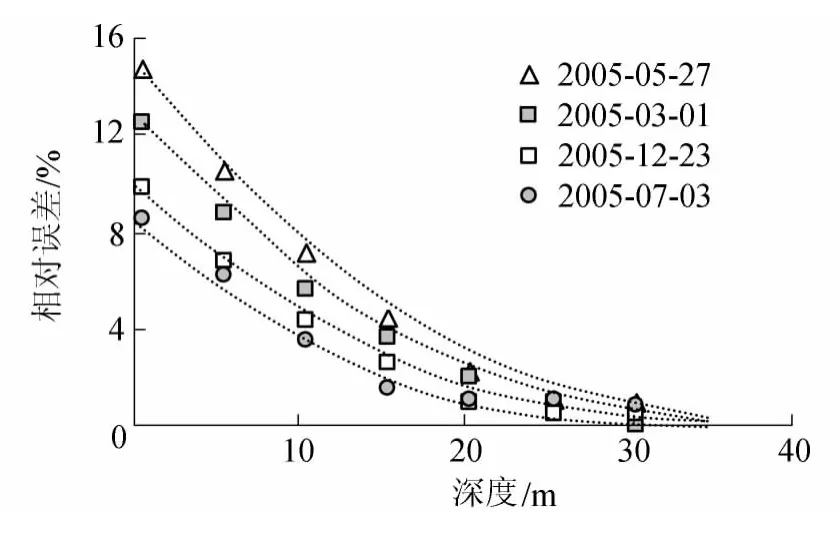
图9 UBM中以曲代直引起的相对误差随深度变化曲线Fig.9 Variation of relative error with depth caused by replacing straight line with curve in UBM

表1 以曲代直简化修正结果与精确修正结果对比分析及误差评估Table 1 Comparison of two correction results based on UBM and error evaluation

由图9可知:在同一测次中，简化后产生的相对误差随着测斜孔深度增大而增大，这与理论分析结果相同;在不同测次中，简化后产生的相对误差不尽相同，但增长速率基本一致。综上，UBM中以曲代直的方法使深孔测斜观测的误差修正工作量大大简化，有效解决了深孔长时间测试过程中传感器的数据漂移问题。简化修正值大于精确修正值，误差随孔深加大而增加，针对30 m孔深，孔口相对误差小于15%，结果偏于安全。

6 结 论

a.滑动式测斜仪在使用过程中大体存在三类误差，分别为系统误差、人为误差、环境误差。各类误差之间并非孤立，而是相互影响的。

b.UBM能有效消除零点漂移误差。测斜仪测试数据发生零点漂移问题时，可能出现位移曲线方向与实际位移曲线方向相反、位移量值偏大或偏小现象，通过UBM方法可以得到较好修正。

c.UBM中以曲代直简化思想使深孔测斜观测的误差修正工作量大大简化，有效解决了深孔长时间测试过程中传感器的数据漂移问题。简化修正值大于精确修正值，误差随孔深加大而增加，针对30 m孔深，孔口误差小于15%，结果偏于安全。

［1］赵维炳，高俊合，施建勇.软土深基坑施工中深层土体水平位移测试［J］.大坝观测与土工测试，1997，21(4):31-34.(ZHAO Weibing，GAO Junhe，SHI Jianyong.Monitoring techniques for soil lateral movement during the deep excavation［J］.Dam Obseration and Geotechnical Tests，1997，21(4):31-34.(in Chinese))

［2］李瑞娜.测斜仪在监测中的误差分析及控制方法［J］.现代城市轨道交通，2011(增刊1):125-128.(LI Ruina.Inclinometer error analysis and control methods in monitoring［J］.Modern Urban Transit，2011(Sup1):125-128.(in Chinese))

［3］SIMEONI L，MONGIOVI L.Inclinometer monitoring of the Castelrotto landslide in Italy［J］.Journal of Geotechnical and Geoenvironmental Engineering，ASCE，2007，133(6):653-666.

［4］王义峰.基于测斜仪监测成果的蠕变体变形机制分析［J］.岩石力学与工程学报，2009，28(1):212-216.(WANG Yifeng.Analysis of creep deformation mechanism based on inclinometer monitoring results［J］.Chinese Journal of Rock Mechnics and Engineering，2009，28(1):212-215.(in Chinese))

［5］李飞，程鹏怀，单海银.软基路基侧向变形测试分析与限制研究［J］.岩石力学与工程学报，2004，23(12):2114-2117.(LI Fei，CHENG Penghuai，SHAN Haiyin.Testing study on lateral deformation of soft road ground and its control［J］.Chinese Journal of Rock Mechnics and Engineering，2004，23(12):2114-2117.(in Chinese))

［6］刘金龙，朱建群，王吉利，等.测斜仪在路基水平位移监测中的若干问题探讨［J］.湖南科技大学学报:自然科学版，2007，22(3):71-76.(LIU Jinlong，ZHU Jianqun，WANG Jili，et al.Study on some issues of soil inclinometer in monitoring lateral displacement of soft soil foundation under embankment［J］.Journal of Hunan University of Science＆Technology:Natural Science Edition，2007，22(3):71-76.(in Chinese))

［7］张斌.浅谈测斜监测技术在某超大深基坑中的应用［J］.施工技术，2011，40(增刊2):28-31.(ZHANG Bin.Inclining monitoring of some super-large deep foundation excavation［J］.Construction Technology，2011，40(Sup2):28-31.(in Chinese))

［8］汤国起，肖圣泗.钻孔测斜技术的现状与开发应用前景［J］.探矿工程，1999(增刊1):235-238.(TANG Guoqi，XIAO Shengsi.Borehole inclinometer technology status and development prospect［J］.Exploration Engineering，1999(Sup1):235-238.(in Chinese))

［9］王虎子.软土地基大变形位移计和滑动式智能测斜仪研制［D］.南京:河海大学，2011.

［10］靳晓光，李晓红，王兰生.滑坡钻孔测斜量测及数据处理［J］.成都理工学院学报，2002，29(2):217-220.(JIN Xiaoguang，LI Xiaohong，WANG Lansheng.Monitoring of borehole inclination and data handling of landslide［J］.Journal of Chengdu University of Technology，2002，29(2):217-220.(in Chinese))

［11］吴逸，孙冰洋.小波减噪在测斜监测数据处理中的运用［J］.甘肃水利水电技术，2011，47(1):26-28.(WU Yi，SUN Bingyang.Application of wavelet denoising method in inclinometer monitoring data processing［J］.Gansu Water Conservancy and Hydropower Technology，2011，47(1):26-28.(in Chinese))

［12］叶峰，李进辉，张功新.测斜仪使用及数据处理中的若干问题研究［J］.土工基础，2010，24(5):76-81.(YE Feng，LI Jinghui，ZHANG Gongxin.Research on some problems by using inclinometer and data processing［J］.Soil Engineering and Foundation，2010，24(5):76-81.(in Chinese))

［13］方大勇.边坡长期监测中测斜仪测量数据的修正［J］.水电自动化与大坝监测，2006，30(4):56-58.(FANG Dayong.Inclino meter data correction in long-term slope monito-ring［J］.Automation and Dam Monitoring，2006，30(4):56-58.(in Chinese))

［14］LEI G H，AI Y B，SHI J Y.The interpretation of pendulum-type inclinometer readings［J］.Canadian Geotechnical Journal，2006，43(2):210-216.

［15］林宗元.岩土工程试验监测手册［M］.北京:中国建筑工业出版社，2005.

［16］王继华，彭振斌，杜长学，等.浅析测斜仪监测原理和应用［J］.勘察科学技术，2005(2).(WANGJihua，PENGZhenbin，DU Changxue，et al.Discussion on test principle and application of inclinometer［J］.Site Investgation Sicience and Techonlogy，2005(2):55-58.(in Chinese))

［17］STARK T D，CHOI H.Slope inclinometers for landslides［J］.Landslides，2008，5(3):339-350.

［18］葛折圣，黄晓明，王自成.土体测斜仪在软基段路基变形检测中的应用［J］.公路交通科技.2003，20(4):26-29.(GE Zhesheng，HUANG Xiaoming，WANG Zicheng.Soil inclinometer in monitoring horizontal displacement and settlement of soft ground embarkment［J］.Journal of Highway and Transprotation Research and Development，2003，20(4):26-29.(in Chinese))

［19］彭立威.钻孔测斜仪数据处理系统的开发与监测结果分析方法研究［D］.成都:成都理工大学，2011.